Boletín de la Sociedad Geológica Mexicana Volumen 76, núm. 2, A081223, 2024 http://dx.doi.org/10.18268/BSGM2024v76n2a081223

Clasificación semi-supervisada de mezclas de distribuciones para determinar procedencias de artefactos de obsidiana en Izapa, Chiapas

Semi-supervised classification of distribution mixtures to determine the sources of obsidian artifacts at Izapa, Chiapas

Pedro A. López García¹, Denisse L. Argote Espino^2,*, Alejandro J. Uriarte Torres²,

Ivonne A. Pérez Alcántara³, Gerardo Cifuentes Nava⁴

¹ Posgrado de Arqueología, Escuela Nacional de Antropología e Historia. Periférico Sur y Zapote s/n, Colonia Isidro Fabela, 14030 Tlalpan, CDMX, México.

² Dirección de Estudios Arqueológicos, Instituto Nacional de Antropología e Historia. Calle Tacuba 76, 4to piso, Colonia Centro, 06000 Cuauhtémoc, CDMX, México.

³ Centro INAH San Luis Potosí. Arista No. 933, Colonia Tequisquiapan, 78230 San Luis Potosí, San Luis Potosí , México.

⁴ Instituto de Geofísica, Universidad Nacional Autónoma de México. Circuito de Investigación, Ciudad Universitaria, 04510 Coyoacán, CDMX, México.

* Autor para correspondencia: (D.L. Argote Espino) This email address is being protected from spambots. You need JavaScript enabled to view it.

Cómo citar este artículo:

López García, P.A., Argote Espino, D.L., Uriarte Torres, A.J., Pérez Alcántara, I.A., Cifuentes Nava, G., 2024, Clasificación semi-supervisada de mezclas de distribuciones para determinar procedencias de artefactos de obsidiana en Izapa, Chiapas: Boletín de la Sociedad Geológica Mexicana, 76 (2), A081223. http://dx.doi.org/10.18268/BSGM2024v76n2a081223

Manuscrito recibido: 12 de Septiembre de 2023; manuscrito corregido: 8 de Octubre de 2023; manuscrito aceptado: 12 de Octubre de 2023.

RESUMEN

La caracterización química de materiales recuperados de sitios arqueológicos ha sido utilizada para relacionar artefactos con sus respectivas fuentes de materia prima. Para ello, comúnmente se emplean métodos convencionales de la estadística clásica, como son los gráficos bivariados, el análisis de conglomerados y las transformaciones lineales de datos. Quienes han aplicado estos métodos afirman tener un alto grado de confianza en la correcta asignación de los materiales a sus respectivas fuentes. Sin embargo, si los datos empíricos se desvían de los supuestos teóricos, las técnicas de estadística clásica pueden producir asignaciones incorrectas. En este trabajo, se propone un procedimiento de aprendizaje semi-supervisado utilizando el agrupamiento y la clasificación basados en modelos de mezclas de distribuciones exponenciales de potencia asimétricas multivariantes. El objetivo es rastrear el origen y procedencia de los materiales arqueológicos de obsidiana de la zona arqueológica de Izapa, Chiapas, optimizando significativamente el resultado de la correcta asignación de datos sin etiquetar al emplear únicamente una supervisión limitada en forma de instancias etiquetadas. La comprobación de la eficacia del método propuesto se realizó primeramente mediante un experimento controlado utilizando muestras geológicas de yacimientos de obsidiana. Posteriormente, se aplicó el método para analizar un conjunto de artefactos de obsidiana recolectados en excavaciones dentro del sitio de Izapa fechadas para el periodo Clásico. En ambos casos, se obtuvieron clasificaciones bien definidas que, para el caso de Izapa, permitieron determinar el consumo de materiales procedentes de fuentes de Guatemala, así como cierta relación con fuentes del occidente y centro de México.

Palabras clave: Análisis de procedencia de obsidianas; Zona arqueológica de Izapa; Fluorescencia de rayos X portátil; Clasificación semi-supervisada; Agrupación basada en modelos; Modelo de mezcla finita.

ABSTRACT

The chemical characterization of materials recovered from archaeological sites has been used to relate artifacts to their respective sources of raw material. For this, conventional methods of classical statistics are commonly used, such as bivariate graphs, cluster analysis and linear data transformations. Those who have applied these methods claim to have a high degree of confidence in the correct assignment of materials to their respective sources. However, if empirical data deviate from theoretical assumptions, classical statistical techniques can produce incorrect assignments. In this paper, we propose a semi-supervised learning procedure using clustering and classification based on models of mixtures of multivariate asymmetric exponential power distributions. The objective is to trace the origin and provenance of obsidian archaeological materials from the archaeological zone of Izapa, Chiapas, significantly optimizing the result of the correct allocation of unlabeled data by employing only limited supervision in the form of labeled instances. The effectiveness of the proposed method was evaluated by a controlled experiment using data from a set of geological samples from obsidian deposits. Subsequently, the method was applied to analyze a set of obsidian artifacts collected in excavations within Izapa dated for the Classic period. In both cases, well-defined classifications were obtained that, in the case of Izapa, allowed to determine the consumption of materials from Guatemalan sources, as well as some relationship with sources from western and central Mexico.

Keywords: Obsidian provenance analysis; Archaeological zone of Izapa; Portable X-ray fluorescence; Semi-supervised classification; Model-based clustering; Finite mixture models.

1. Introducción

Determinar el origen o procedencia de los artefactos arqueológicos que son recuperados en los sitios arqueológicos ha servido para establecer cuáles eran las materias primas seleccionadas por los pueblos antiguos y sus principales fuentes de abastecimiento. Esto ha permitido a los arqueólogos reconstruir redes comerciales (Tykot, 2016), establecer cambios en las prácticas de selección de materiales, determinar el uso de diferentes fuentes naturales de abastecimiento lo largo del tiempo, así como poder inferir el control político en la explotación de dichas fuentes (Baxter et al., 2003; Glascock, 1992). Sin embargo, para hacer la asignación de los materiales arqueológicos a sus yacimientos naturales se han usado procedimientos poco confiables, entre los que se incluye a los métodos visuales (Pierce, 2015; Braswell et al., 2000), gráficos bivariables usando datos sin transformar (Moholy-Nagy et al., 2013; Tykot, 2016; Glascock, 2010), análisis de componentes principales (ACP) en datos sin transformar (Tykot, 2016), ACP con datos estandarizados (Petřík et al., 2020), ACP con datos transformados a log₁₀ (Cohen y Pierce, 2018; Glascock et al., 1998; Hall, 2004; Hall y Minyaev, 2002; Millhauser, et al., 2011), análisis discriminante en datos sin transformar (Tykot, 2016), análisis de correspondencias en datos estandarizados (Petřík et al., 2020), análisis de conglomerados (Moholy-Nagy et al., 2013; Petřík et al., 2020), y distancia de Mahalanobis (Carr, 2015; Cohen y Pierce, 2018; Glascock, 1992; Hodge et al., 1992), principalmente.

En la práctica, hemos podido comprobar que la mayoría de los estudios sobre procedencia se limitan únicamente a la parte exploratoria y a la descripción de datos, mientras que la validación estadística de los resultados raramente es abordada (Kovarovic et al., 2011; Charlton et al., 2012; Resler et al., 2021). Existen dos enfoques principales en los estudios de procedencia. El primero afirma que, para lograr un estudio exitoso de caracterización química, es necesaria la inclusión del mayor número de elementos en el análisis para lograr una separación efectiva de los grupos químicos. Al respecto, Harbottle (1982) argumenta que las clasificaciones basadas en numerosos elementos son superiores a las basadas en unos pocos. La inclusión de todas las componentes obedece a la idea de que no será posible obtener un resultado óptimo si solamente se analiza un número limitado de elementos, ya que se desconoce a priori cuales de las componentes podrían ser más efectivas para la discriminación de estos grupos. De igual manera, Glascock (1992) afirma que “es recomendable utilizar la información de todos los elementos... utilizar la máxima cantidad de información”. En consecuencia, Glascock y sus partidarios a menudo usan ≥ 20 elementos en las atribuciones de fuentes (Glascock, 1992; Glascock y Neff, 2003).

El segundo enfoque implica la selección crítica de elementos. Baxter y Jackson (2001) señalaron que la selección de variables es inevitable en los análisis composicionales. Hughes (1984, p. 3) sostiene que “la inclusión de un mayor número de variables […] no necesariamente resulta en una ‘mejor’ clasificación” y señala que deben eliminarse los elementos mal medidos, redundantes o poco informativos; de otra forma, se corre el riesgo de sesgar de forma engañosa el análisis y aumentar el número de clasificaciones erróneas (Shackley, 1988). Desafortunadamente, el criterio de selección de variables ha variado de una investigación a otra de acuerdo con el juicio personal de cada investigador. Por ejemplo, Shackley (1994) propone utilizar únicamente cuatro elementos (Ba, Rb, Sr, Zr) como los más diagnósticos en la obsidiana, mientras que Ferguson (2012) afirma que sólo seis elementos (Fe, Rb, Sr, Y, Zr y Nb) son los más relevantes. Sin embargo, en estas aproximaciones no se discute a detalle cuales son los criterios para llegar a tales afirmaciones, probablemente basándose solo en la experimentación personal y sin ningún soporte formal o tipo de validación.

Podemos concluir que ninguno de estos enfoques es totalmente correcto y, en los casos en donde se afirma que se han identificado con éxito las fuentes, habría que poner en duda los resultados ya que en ninguno de estos se lleva a cabo un criterio de validación. Esto deja en entredicho las posibilidades de reproducibilidad en otras investigaciones en donde se utilicen nuevos datos para responder a la misma pregunta científica. Por otro lado, además de considerar la inclusión o exclusión de variables en los estudios de procedencia, se debe tomar en cuenta el o los algoritmos de agrupación o clasificación. Los métodos multivariados más utilizados en los estudios de procedencia pueden ser de dos tipos: los supervisados y los no supervisados. Entre los métodos no supervisados preferidos están el análisis de componentes principales y el análisis de conglomerados, mientras que en los métodos supervisados se incluyen el análisis discriminante, los árboles de decisión, la máquina vectorial de soporte (support vector machine) o el algoritmo de KNN (K-Nearest Neighbor). Sin embargo, estos métodos poseen diversos inconvenientes.

Los métodos no supervisados implican que no se dispone de información a priori sobre la pertenencia a los grupos para ninguna de las observaciones. En este caso, el procedimiento de clasificación genera automáticamente las clases. El objetivo de los métodos no supervisados es dividir el conjunto de datos que conforman un grupo heterogéneo en subconjuntos homogéneos entre sí y diferentes de los pertenecientes a otros grupos. Estos métodos se consideran de tipo exploratorio y utilizan distancias como medida de similitud para conformar los grupos; debido a la gran cantidad de métricas utilizadas y a los diferentes métodos de agrupación, se ha podido comprobar que se puede llegar a resultados muy diferentes al aplicar distintas técnicas incluso utilizando el mismo conjunto de datos (Templ et al., 2008). Otro inconveniente de estas técnicas es que, aunque los datos no contengan una estructura de grupo, el algoritmo de conglomerados producirá grupos, además de ser incapaces de determinar el número de grupos en el conjunto de datos.

Obviamente, si los datos contienen variables redundantes o con ruido, el agrupamiento será diferente a si sólo se incluyen las variables relevantes. Además, se debe tener en cuenta que los resultados de un análisis de conglomerados “…nunca puede ser una prueba estadística de una cierta relación entre las variables u observaciones…” (Templ et al., 2008, p. 2). En el caso del ACP, se tiene el inconveniente de que es muy sensible a las unidades de medida, ya que las primeras componentes estarán dominadas por qué aquellas variables que tienen una varianza mayor. Por otro lado, si los datos están fuertemente correlacionados o si las variables no se distribuyen linealmente, el ACP resulta ser un método inadecuado. Por otro lado, el ACP es muy sensible ante la presencia de valores atípicos y, contrario a lo que se cree, a menudo incurre en una pérdida de información al eliminar los datos que no se encuentran en las primeras dos o tres.

Para el caso de la clasificación supervisada, se dispone de un conjunto de datos de entrenamiento cuya etiqueta es conocida. En la fase de entrenamiento se construye un modelo utilizando el etiquetado de los datos, el cual nos indica si una muestra está clasificada correcta o incorrectamente por el modelo. Una vez construido el modelo, este se puede utilizar para clasificar nuevos datos cuyas etiquetas se desconocen. Sin embargo, el aprendizaje supervisado adolece en muchos dominios de la falta de suficientes ejemplos de entrenamiento para generar un modelo eficaz. Además, si los grupos no están balanceados, aquellos con un mayor número de observaciones tendrán un impacto significativo en los resultados. En este caso, también aplica el manejo de información redundante, del ruido y de la información irrelevante, por lo que es necesario incluir sólo las características que están relacionadas o conducen a las clases de aprendizaje supervisado.

Por otro lado, si no se respetan los supuestos teóricos del modelo, como la normalidad de las variables u la homogeneidad de varianza de los grupos, estos métodos tienden a producir resultados poco fiables. Por lo que, para tener éxito y poder hacer una asignación correcta de las unidades experimentales a los grupos, deben considerarse varios factores sustanciales. Por ejemplo, en casos de alta dimensionalidad, se debe incluir un procedimiento de selección de variables relevantes con respaldo probabilístico para eliminar variables redundantes o con ruido que puedan afectar el análisis (López-García y Argote, 2023). Otros factores de suma importancia son la transformación aplicada a los datos composicionales, el diagnóstico de los datos para detectar la existencia de valores atípicos o outliers y el o los algoritmos utilizados para agrupar/clasificar las unidades experimentales.

En el caso de la selección de variables, actualmente existen métodos diseñados para identificar objetivamente las componentes más informativas y que más contribuyen a la agrupación o clasificación. Estos son los métodos de agrupamiento basados en modelos de mezcla finita, los cuales ubican la tarea de agrupamiento en un marco formal en donde la distribución empírica de datos se ajusta a través de una mezcla finita de distribuciones teóricas de probabilidad, típicamente la distribución gaussiana multivariante (Banfield y Raftery 1993; Fop y Murphy, 2018). En este artículo, abordamos el problema de la procedencia utilizando un algoritmo semi-supervisado, cuyo principio se basa en el cálculo de probabilidades derivados de la agrupación basada en modelos. Este tipo de aproximación hace uso del etiquetado parcial de datos, el cual es más flexible y robusto en comparación con los métodos supervisados y no supervisados, siendo capaz de resolver los problemas de traslapes totales o parciales en los datos composicionales observados frecuentemente en los gráficos bidimensionales o en las proyecciones obtenidas por métodos lineales. De esta forma, se pueden realizar inferencias sobre datos de interés arqueológico con un alto grado de certeza, como se demostrará más adelante.

2. Metodología

2.1. Datos que contienen información relativa

Los datos composicionales cuentan con una estructura geométrica algebraica diferente a la de los datos reales (R^D). Los datos composicionales son vectores que muestran la importancia relativa de las partes de un todo (Egozcue y Pawlowsky-Glahn, 2011). En general, los datos composicionales se pueden definir como un vector de D-partes x = (x₁,…, x_D) de valores estrictamente positivos, donde la información relevante está en las relaciones entre las partes (Egozcue y Pawlowsky-Glahn, 2016). Estos datos están contenidos en Simplex (S^D), que es un espacio acotado con una restricción de suma constante, en el que se aplica la geometría de Aitchison. Sin embargo, los métodos estadísticos estándar están diseñados para funcionar en geometría euclidiana clásica en (R^D) o espacios p-dimensionales no restringidos (Aitchinson, 1986; Palarea-Albaladejo y Martín-Fernández, 2020) y no en la geometría de Aitchison. Si no se toma en cuenta que los datos composicionales son datos cerrados y su espacio nativo es el Simplex se pueden producir resultados engañosos con su aplicación a datos de composición sin procesamiento adecuado (Egozcue et al., 2003; Egozcue y Pawlowsky-Glahn, 2011; Filzmoser et al., 2009; Hron et al., 2012; Korhonová et al., 2009; Pawlowsky-Glahn y Buccianti, 2011).

La geometría de Aitchison posee todas las propiedades habituales de la geometría euclidiana, respetando la naturaleza relativa de los datos y cumpliendo los requisitos para operaciones en un espacio vectorial (Aitchison, 1986; Egozcue y Pawlowsky-Glahn, 2005). La transformación de los datos composicionales al espacio real multivariante se basa en los logaritmos de los cocientes entre las partes de un dato composicional (Mateu-Figueras et al., 2003). Aitchison (1986) propone tres tipos de transformaciones de los datos basadas en los logaritmos de cocientes entre las partes de un dato composicional. Estas transformaciones incluyen el log-cociente aditiva (alr), log-cociente centrado (clr), y el log-cociente isomérico (ilr), como se explica en Pawlowsky-Glahn y Buccianti (2011). Usando las transformaciones de tipo log-cocientes (log-ratios) es posible convertir los datos composicionales del espacio de muestra del simplex en espacio de muestra real/euclidiano.

En este estudio, se utilizó el algoritmo del log-cociente centrado (clr), reescalando previamente los datos mediante el operador de clausura C (Mateu-Figueras et al., 2003). La transformación clr mapea isométricamente una composición de D-partes del Simplex a un sub-espacio vectorial euclidiano D-dimensional, manteniendo el número original de componentes. “Su imagen es el hiperplano de R^D que pasa por el origen y es ortogonal al vector de unidades, es decir, la suma de las componentes del vector transformado es igual a cero” (Mateu-Figueras et al., 2003, p. 6). La transformación clr es utilizada para definir una estructura métrica en S^D; de manera análoga, se puede definir a E{clr (x)} y cov{clr( x)}, donde E corresponde al valor esperado y cov corresponde a la matriz de covarianza de las componentes. En la geometría de Atchison, las diferencias relativas se utilizan para expresar distancias entre las observaciones.

2.2. Agrupamiento Basado en Modelos

El agrupamiento basado en modelos (MBC, acrónimo del inglés Model-based Clustering) permite llevar a cabo un planteamiento formal basado en modelos probabilísticos del aprendizaje de los diferentes sistemas de clasificación, como la clasificación no-supervisada, semi-supervisada y supervisada. El MBC se refiere a la práctica de ajustar un modelo de mezcla finita a los datos para determinar el número de componentes y estimar la membresía de pertenencia de cada unidad experimental a los grupos a partir del conjunto de datos (Dang, 2014). Cuando se trabaja con poblaciones finitas, como en el caso de los yacimientos de obsidiana, no es posible modelar el conjunto de muestras a partir de una única distribución, por lo que es más conveniente utilizar una combinación de ellas. En este sentido, se considera que tales datos provienen de distintos grupos; es decir, subpoblaciones asociadas a distintos procesos generadores que se corresponden con las componentes de la mezcla y cuya pertenencia a uno u otro grupo se desconoce.

La distribución (Dⁿ) paramétrica más popular es el modelo de mezclas Gaussianas finitas (GMM, acrónimo del inglés Gaussian Mixture Model), que representa la existencia de subpoblaciones (llamadas componentes) mediante una función de densidad de probabilidad dentro de la misma población. Empero, se debe considerar que las distribuciones empíricas de los datos composicionales están fuertemente sesgadas y con frecuencia no satisfacen el supuesto de la distribución subyacente del modelo de mezclas Gaussiano. Reimann y Filtzmoser (2000) han podido demostrar que la mayoría de los conjuntos de datos geoquímicos se desvían de la normal o logarítmica normal y que más del 70% de todas las componentes en cada conjunto de datos químicos se desvían de la Dⁿ normal. Esto se puede comprobar fácilmente en cualquier base de datos usando métodos gráficos, como los histogramas, los gráficos de comparación de cuantiles (Q-Q plots) o las pruebas de contraste de normalidad como la prueba de Kolmogorov-Smirnov o la de Shapiro-Wilk.

Con el fin de satisfacer el supuesto de normalidad, es común aplicar algún tipo de transformación a los datos. Baxter y Buck (2000) recomiendan la estandarización de los datos químicos, lo que equivale a una transformación lineal z = en donde es el valor original de la variable, es la media de la variable y es la desviación estándar. Esta transformación no resulta ser suficiente para modificar rasgos más complejos de una distribución como, por ejemplo, la asimetría. Reimann et al. (2002) afirman que la estandarización Z tiene poco sentido en geoquímica porque se sabe que las distribuciones empíricas de los datos están fuertemente sesgadas. Por otro lado, la transformación de datos a log₁₀ es la forma más utilizada por el laboratorio de la Missouri University Research Reactor o MURR (Glascock, 1992; Hodge et al., 1992), de la cual se afirma evitar que algunas de las componentes tengan un mayor peso y puedan tener un papel dominante en una clasificación; además, se asevera que la tendencia de los datos se aproxima más a la normalidad para el caso de los elementos traza. En lugar de forzar los datos a la simetría, es recomendable representar los datos composicionales en coordenadas reales antes de comenzar con un análisis estadístico.

Los GMM imponen la restricción de que las componentes de la muestra asociadas a un conglomerado se deban ajustar a la función de densidad de probabilidad (FDP) de una forma elíptica, tomando en cuenta solamente los parámetros de locación (μ) y de dispersión (Σ) que corresponden al vector de medias y a la matriz de covarianzas. En muchos casos, resulta adecuado modelar los datos como una mezcla de varias densidades simétricas como la gaussiana (Morris et al., 2019). No obstante, cuando las componentes no se ajustan al modelo Gaussiano y presentan un mayor grado de asimetría con distribuciones platicúrticas o leptocúrticas de conglomerados, se sabe que el modelo gaussiano puede dar como resultado una sobreestimación del número de componentes, lo que ocasiona un ajuste excesivo del modelo (Dang, 2014; Dang et al., 2023; Franczak et al., 2014). Otro factor que puede influir en un número excesivo de componentes es que los datos estén contaminados con valores atípicos o extremos, ya que estos siempre tienen un efecto negativo en la estimación de los parámetros (Morris et al., 2019).

Además de la Dⁿ Gaussiana, actualmente existen algunas variantes de los modelos de mezclas que consideran la asimetría en los grupos, usando distribuciones más flexibles para la agrupación. Estos modelos pueden manejar una combinación de distribuciones platicúrticas y leptocúrticas. Las distribuciones platicúrticas tienen colas más delgadas que la Dⁿ Gaussiana, es decir, presentan un reducido grado de concentración alrededor de los valores centrales de la variable. Las leptocúrticas se caracterizan por ser distribuciones con curtosis positiva mayor que la Dⁿ normal; éstas tienen colas más anchas o pesadas, por lo que pueden contener una mayor probabilidad de manejar los valores atípicos a diferencia de las distribuciones mesocúrticas o platicúrticas. En este tenor, Dang et al. (2023) proponen el uso de una familia de mezclas exponenciales que permite modelar mezclas de distribuciones sesgadas, tomando en cuenta la asimetría, el peso variable de las colas y el pico de los datos. Este tipo de distribuciones es más adecuado porque no sobreajustan los datos al incluir componentes adicionales para capturar la asimetría.

Dang et al. (2023) formulan el uso de la mezcla de distribuciones Multivariadas de Potencia Exponenciales (MPE). Es decir, se considera un modelo de mezclas basadas en una Dⁿ de potencia exponencial sesgada multivariante; esta Dⁿ es útil para modelar las desviaciones de la normalidad en los datos por medio de un parámetro escalar ( β ) de peso de cola que regula la no normalidad del modelo. Para la estimación de parámetros en los modelos de mezcla, es común utilizar el algoritmo de Expectation–Maximization (EM), el cual es un método iterativo para realizar una estimación de máxima verosimilitud de parámetros en situaciones en las que existen datos incompletos o que son tratados como incompletos. Sin embargo, el EM es muy sensible a la inicialización y, por tratarse de un método local, no garantiza encontrar la mejor solución global. Es por ello que Dang et al. (2023) utilizan en su lugar un algoritmo de maximización de expectativas generalizadas (GEM) con pasos de maximización condicional (Dempster et al., 1977; citado por Dang et al., 2023).

La ventaja del GEM es que “los pasos de maximización condicional aumentan, en lugar de maximizar, el valor condicional esperado del logaritmo de la verosimilitud de los datos completos en cada iteración del algoritmo” (Dang et al., 2023, p.5). Para optimizar la inicialización del algoritmo GEM, es necesario obtener un buen conjunto de parámetros de partida. Para ello, Dang et al. (2023) proponen el enfoque emEM desarrollado originalmente por Biernacki et al. (2003), el cual es un método de inicialización aleatoria que utiliza un algoritmo de clasificación EM y se compone de pasos EM cortos y EM largos. El paso EM corto implica comenzar desde varios puntos aleatorios y ejecutar el algoritmo EM hasta que se cumpla algún criterio de convergencia laxo. La solución que produce la probabilidad logarítmica más alta se elige como punto de partida para la segunda etapa llamada EM larga, la cual se ejecuta hasta que se cumplen los estrictos criterios de convergencia habituales (Melnykov, 2010).

Concluida la inicialización y para poder predecir los valores numéricos y las etiquetas de clase en las estimaciones de máxima verosimilitud de los parámetros del modelo, se calcula el paso-E del algoritmo GEM. En este, las estimaciones de las membresías de pertenencia al grupo _ig se actualizan para i = 1, …, n y g = 1,…, G, donde _ig = 1 si se encuentra en el grupo G y _ig = 0. Con el paso M se actualizan las proporciones de la mezcla. Bajo una variedad de estructuras de covarianza, el modelo es capaz de establecer una familia de 16 modelos de mezcla de MPE para usar tanto en el agrupamiento como en la clasificación semi-supervisada (Dang et al., 2023).

2.3. Selección de Modelos

En una distribución Multivariante Sesgada de Potencia Exponencial (MSPE), se utiliza el criterio de información bayesiano (BIC) para elegir el modelo de mejor ajuste de entre una familia de modelos (Schwarz, 1978). El BIC se puede obtener mediante el uso de factores de Bayes. Como en este caso se tienen modelos alternativos (M₁, M₂, … , el objetivo es elegir el modelo con el mejor ajuste para el conjunto de datos. El BIC es un criterio estadístico de evaluación de modelos en términos de sus probabilidades posteriores que permite identificar y seleccionar el óptimo de entre una familia de 16 modelos MSPE, así como estimar el número óptimo de componentes de la mezcla. La estimación de máxima verosimilitud y la estimación máxima a posteriori (MAP) de los parámetros de los modelos de la agrupación se realizan utilizando el algoritmo GEM para los problemas de datos incompletos. El algoritmo se ejecuta en varios modelos con restricciones en las matrices de covarianza de los grupos; el modelo que mejor ajusta a los datos se elegirá de la combinación del modelo y número de grupos que conduzcan al valor de BIC más alto. Kass y Raftery (1995), entre otros autores, definen al BIC como de signo opuesto al obtenido por el MSPE, en cuyo caso entre más pequeño sea el BIC, más fuerte será la evidencia a favor del modelo.

2.4 Descripción del paquete ‘mixSPE’ para R

El lenguaje de programación R (R Core Team, 2020) ofrece un conjunto de algoritmos para realizar el aprendizaje semi-supervisado y la agrupación basada en modelos, incluyendo el paquete ‘mixSPE’ versión 0.9.1 (Browne et al., 2022). Mediante la función ‘EMGr ()’, este paquete permite aplicar los métodos basados en mezclas de distribuciones multivariadas de potencia exponencial (MPE) y de potencia exponencial sesgada (MSPE) para clasificar los datos no etiquetados. Aquí, los parámetros que se deben establecer son los siguientes: G (2-n), que corresponde al número de componentes que se desean ajustar en la mezcla; iModel, que es el modelo de arranque utilizado para generar estimaciones de parámetros iniciales; label = (“), que corresponde al vector de las etiquetas de cada clase, incluyendo el 0 para aquellas observaciones no etiquetadas; y modelSet para establecer el ajuste de alguno de los 16 modelos. En el caso de este último, configurar modelSet = “all” va a ajustar todos los modelos automáticamente. De lo contrario, se puede proporcionar un vector de caracteres de un subconjunto de estos modelos: “EIIE”, “VIIE”, “EEIE”, “VVIE”, “EEEE”, “EEVE”, “VVEE”, “VVVE”, “EIIV”, “VIIV”, “EEIV”, “VVIV”, “EEEV”, “EEVV”, “VVEV”, “VVVV”.

Cada una de las letras anteriores corresponde a las restricciones impuestas en las matrices de covarianza e indican el tipo de volumen, forma y orientación de las componentes (E = equal, V = variable e I = orientation). Dang et al. (2014) denomina a esta familia de modelos como mezcla de potencias de decaimiento exponencial. Para el caso del parámetro Skewness, si se establece como ‘TRUE’, se va a ajustar a las mezclas de distribuciones de potencia exponenciales asimétricas multivariadas que pueden modelar la asimetría de los datos (Browne et al., 2022). Para comprobar la exactitud en la clasificación, los resultados de la asignación del modelo MSPE son comparados con los datos originales utilizando el índice de Rand ajustado (Hubert y Arabie, 1985). Este índice es un medio para comparar la similitud de resultados entre la etiqueta original de las muestras y la asignada por el método de clasificación. El índice Rand siempre toma un valor entre 0 y 1, donde 1 indica que se ha obtenido una clasificación perfecta y 0 indica una clasificación aleatoria (Dang et al., 2023).

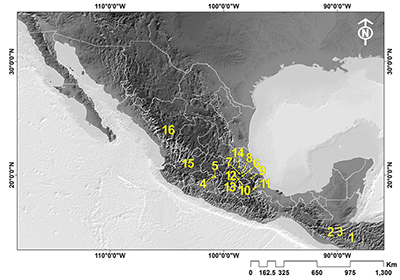Figura 1. Localización geográfica de los yacimientos de obsidiana analizados: 1) Ixtepeque, 2) SMJ, 3) El Chayal, 4) Zinapecuaro, 5) Ucareo, 6) Paredon, 7) Sierra de Pachuca, 8) Tulancingo, 9) Oyameles, 10) Otumba-Malpais, 11) Pico de Orizaba, 12) Otumba-Ixtepec, 13) Otumba-Soltepec, 14) Zacualtipan, 15) Ahuisculco, 16) Llano Grande.

3. Resultados

3.1 Yacimientos de Obsidiana de México y Guatemala

Para evaluar la eficiencia del método, se realizó una primera aproximación recurriendo a datos de concentraciones químicas de muestras cuyo origen fuera conocido, de manera que fungieron como pruebas controladas. Para ello, se utilizaron muestras geológicas recolectadas de 16 fuentes de obsidiana diferentes, 13 correspondían a yacimientos de diferentes regiones de México y 3 a fuentes en Guatemala (Tabla 1; Figura 1). Los datos composicionales, así como descripciones de cada una de las fuentes, pueden consultarse en García Gómez (2018), y López-García et al., (2019; 2021; 2023b). Debido a que el espacio geométrico de los datos composicionales es el Simplex (S^D), los datos fueron transformados al log-cociente centrado. Una amplia discusión sobre los diferentes tipos de transformaciones y los fundamentos teóricos del análisis log-ratio se pueden consultar en López-García et al. (2021) y López-García y Argote (2023). De cada yacimiento se utilizaron 20 muestras, excepto de Otumba_Ixtepec (con n = 14) y de Llano Grande (con n = 15). Cada subconjunto de 20 muestras por yacimiento fue subdividido a su vez en muestras con etiqueta (labeled) y muestras sin etiquetar (unlabeled), asumiendo que la procedencia de este segundo grupo era desconocida.

Tabla 1. Listado de muestras de 16 fuentes diferentes de obsidiana recolectadas en diversas regiones de México y Guatemala.

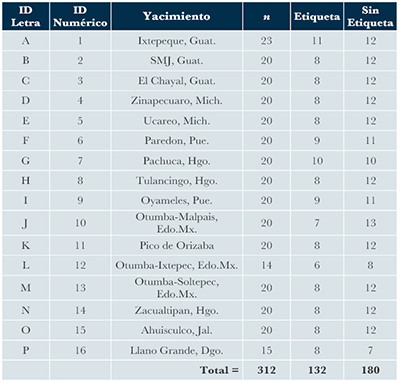En la Tabla 1 puede verse resumida la información arriba descrita: la primeras dos columnas indica la letra y el número asignada para identificar a cada grupo, la tercera describe el nombre del yacimiento del cual se recolectaron las muestras, la cuarta señala el número total de muestras analizadas para cada yacimiento, la quinta columna indica el número de muestras cuya procedencia es conocida (muestras etiquetadas), y la sexta se refiere a las muestras cuyo origen se asume no ser conocido (muestras sin etiquetar). En este ejercicio, el 58% del total de las muestras se manejaron como desconocidas. Para que el algoritmo sea capaz de discriminar entre los datos etiquetados y los no etiquetados, en la matriz de datos debe incluirse un vector que indique la etiqueta numérica que identifica a cada yacimiento (ver Tabla 1 para examinar el identificador numérico de cada yacimiento); notar que el ‘0’ sólo es asignado a aquellas muestras con procedencia desconocida (Tabla 2).

Tabla 2. Etiqueta de las muestras con procedencia conocida y muestras con procedencia desconocida, las últimas identificadas con un 0 (la matriz se lee de izquierda a derecha y de arriba abajo).

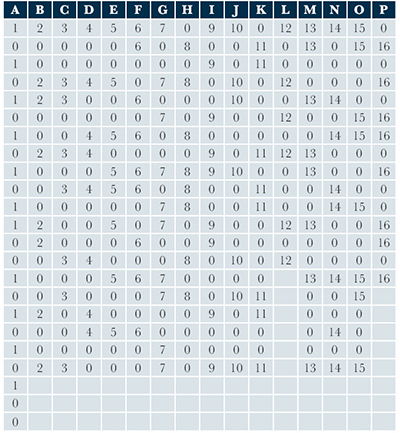Así, si contamos las asignaciones en la Tabla 2, podemos ver que en el grupo A hay 23 muestras de Ixtepeque, de las cuales sólo 11 tienen etiqueta (ID numérico “1”); en el grupo B hay 20 muestras de San Martín Jilotepeque con 8 muestras etiquetadas (ID numérico “2”); y así, lo mismo aplica para el resto de los yacimientos. Como puede apreciarse en la Tabla 1, se manejó un total de n = 180 muestras de origen desconocido. El conocimiento previo de la procedencia de todas las muestras permitió evaluar la exactitud de la clasificación semi-supervisada propuesta para calcular las membresías de pertenencia a los grupos. Usando el código presentado en el Apéndice al final de este artículo, se hizo el ajuste del modelo de mezclas de MSPE. El BIC seleccionó el modelo “EEEEV” con 16 componentes (Tabla 3), el cual implica que el volumen y la forma de los grupos son iguales, sólo variando su orientación.

Tabla 3. BIC calculado para la familia de 16 modelos de MSPE.

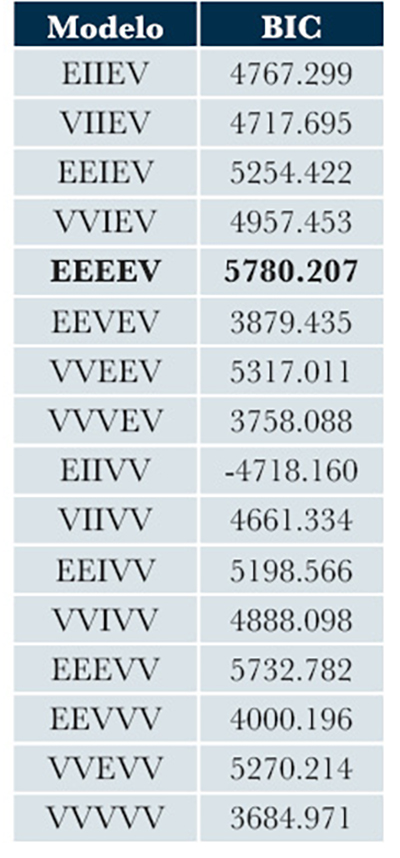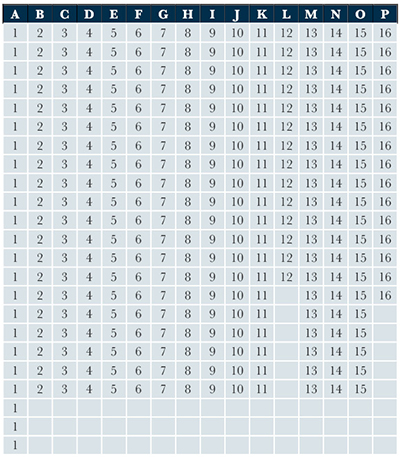
En la Tabla 4 puede apreciarse como el MSPE asignó correctamente todas las muestras a su yacimiento correspondiente. El valor del índice de Rand ajustado para el modelo MSPE seleccionado fue de 1, lo que indica una agrupación perfecta. La efectividad del método se vio comprobada incluso al correrse el algoritmo con sólo tres muestras etiquetadas en cada uno de los yacimientos. Esto demuestra que el tamaño de muestra no es un factor importante en el modelo MSPE para determinar la procedencia de las muestras, al contrario del caso de la Distancia de Mahalanobis en donde hay restricciones con el tamaño de muestra de los grupos. Con base en los resultados obtenidos, se procedió a aplicar el método a datos reales con muestras de obsidiana de origen desconocido recolectadas en un sitio arqueológico, como se muestra a continuación.

Tabla 4. Asignación de grupos realizada por la clasificación semi-supervisada con MSPE (la matriz se lee de izquierda a derecha y de arriba abajo).

3.2 Artefactos de obsidiana de la Zona Arqueológica de Izapa, Chiapas

La zona arqueológica de Izapa se encuentra localizada en la región del Soconusco, al sureste del estado de Chiapas, aproximadamente a 10 km de la ciudad de Tapachula y cerca de la frontera con Guatemala (Figura 2). Si bien las investigaciones arqueológicas en Izapa se remontan a la década de 1940, las intervenciones realizadas por la Fundación Arqueológica del Nuevo Mundo (New World Archaeological Foundation, NWAF) entre 1963 y 1965, permitieron caracterizar su patrón de asentamiento organizado en torno a conjuntos de plaza delimitados por arquitectura monumental sobre un área aproximada de 127 ha, y proponer una secuencia ocupacional que se extendió desde el Preclásico temprano (1800 a.C.) hasta el Postclásico temprano (1200 d.C.) (Lowe, et al., 1982). En la actualidad, la mayor parte del asentamiento está bajo el crecimiento urbano moderno, conservándose sólo 2.88 ha cómo áreas protegidas por el Instituto Nacional de Antropología e Historia (INAH) y abiertas al público (Uriarte y Pérez, 2018).

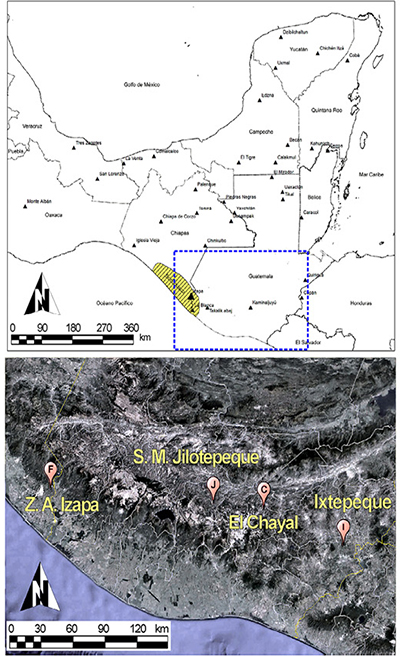Figura 2. Localización de la zona arqueológica de Izapa y su posición con respecto a los tres yacimientos principales de abastecimiento de obsidiana (imagen de satélite obtenida de Google Earth © 2022 Google LLC).

Mendelsohn (2017) realizó un estudio para determinar los yacimientos de obsidiana aprovechados por los habitantes de Izapa, así como los cambios en los patrones de consumo en la transición del Preclásico terminal al Clásico temprano (del 100 a.C. al 400 d.C.), momento durante el cual existieron transformaciones en la organización del asentamiento que resultaron en un aparente abandono de amplios sectores del sitio que habían alcanzado su auge durante el Preclásico tardío (350-100 a.C.) (Lowe et al., 1982). Para su estudio, la autora utilizó materiales procedentes de la excavación de las Estructuras 255 y 260, construcciones de probable función doméstica localizadas al sur del sitio. Por medio de la técnica de fluorescencia de rayos X en su modo portátil, realizó el análisis de 390 navajas de obsidiana y 22 muestras de control de cinco yacimientos (n = 5 de San Martín Jilotepeque, n = 5 de Ixtepeque, n = 5 de El Chayal, n = 5 de Pachuca y n = 2 de Tajumulco). La tabla de concentraciones se puede encontrar en el Apéndice F de Mendelsohn (2017).

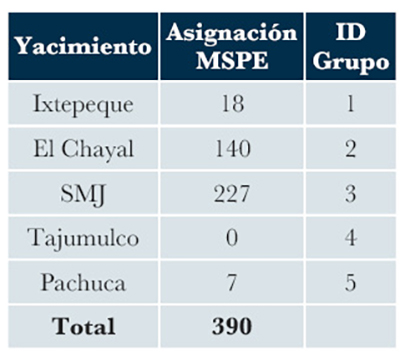
Mendelsohn (2017) utilizó un gráfico bivariable de log₁₀ (Sr) vs log₁₀ (Zr) para asociar las muestras de control con las muestras desconocidas. En sus conclusiones, la autora afirma que hay una clara ausencia de obsidiana de Ixtepeque, predominando la obsidiana de San Martín Jilotepeque (SMJ; 57.4% en promedio del total de navajas analizadas), seguida de la proveniente de El Chayal (17.9% en promedio) y del volcán Tajumulco (8.3% en promedio). Así mismo, hay una baja ocurrencia de obsidiana de Pachuca (5 navajas), junto a 3 muestras que no pudo asignar a ninguna de las fuentes conocidas. Haciendo una clasificación usando el modelo MSPE y transformando los datos al log-ratio isométrico, obtuvimos un resultado diferente al de Mendelsohn (2017), como puede apreciarse en la Tabla 5. Con estos resultados, se confirma que San Martín Jilotepeque era la principal fuente de suministro de Izapa, seguido del El Chayal; lo que sorprende aquí es que, a diferencia de lo afirmado por Mendelsohn (2018), sí se registra presencia de la obsidiana de Ixtepeque y no de Tajumulco.

Tabla 5. Reclasificación usando el modelo MSPE de las muestras de obsidiana analizadas por Mendelsohn (2018).

Lo anterior indicaría una mayor explotación y distribución del yacimiento de Ixtepeque de lo que anteriormente se consideraba para el periodo Preclásico terminal o Protoclásico. Por otro lado, la ausencia de obsidiana del volcán Tajumulco es lógica ya que, a pesar de su cercanía con el sitio (32 km en línea recta), la obsidiana de este volcán posee una baja calidad para la producción de navajas prismáticas, con una textura más granular y una matriz burda (Clark et al., 1989). De ahí la necesidad de los pobladores prehispánicos de importar este bien desde otras regiones un poco más lejanas, como El Chayal, Ixtepeque y San Martín Jilotepeque. Consideramos que la diferencia en los resultados de Mendelsohn (2017) con los nuestros se puede deber a que, tanto la transformación a log10 como el uso de gráficos bivariados, no son el procedimiento indicado para determinar la procedencia de materiales arqueológicos.

Para el presente estudio, se empleó una muestra de 88 artefactos de obsidiana, principalmente fragmentos de navajas prismáticas y lascas, recuperados de las intervenciones arqueológicas efectuadas entre 2017 y 2019 por el Proyecto Investigación y Conservación de Izapa del INAH en las Estructuras 125 y 130 del Grupo F de Izapa. El conjunto arquitectónico del Grupo F se sitúa al norte de la zona arqueológica de Izapa y se caracteriza por su organización en torno a una plaza rectangular con un área de 3.4 ha (Figura 3). Al interior de la plaza, se dispuso un grupo de edificaciones monumentales, entre las que se encuentran las Estructuras 125 y 130 (Lowe et al., 1982). Trabajos previos en el Grupo F permitieron proponer una ocupación que inició durante el periodo Protoclásico (50 a.C.-100 d.C.) y que se intensificó durante el Clásico temprano, alcanzando su mayor extensión durante el Clásico tardío y concluyendo durante el Posclásico temprano (900-1200 d.C.) (Lowe et al., 1982; Rosenswig y Mendelsohn, 2016). Durante estos periodos, el Grupo F se desempeñó como el principal centro cívico-ritual de Izapa, por lo que el análisis de procedencia de los artefactos estudiados proporcionaría información relevante para la comprensión de las redes de intercambio en las que participó el asentamiento entre el Clásico temprano y tardío (del 100 al 900 d.C.).

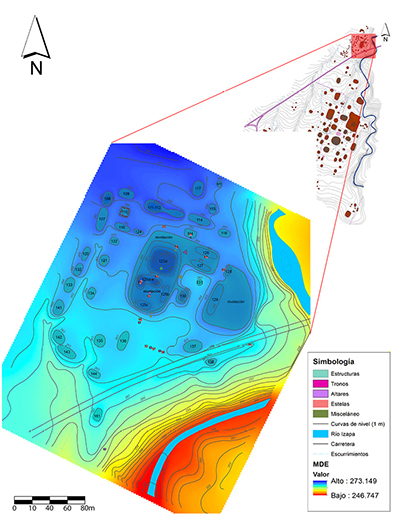Figura 3. Ubicación del Grupo F dentro de la zona arqueológica de Izapa (modificado de Lowe et al., 1982).

En la Figura 4 puede apreciarse los puntos dentro de la zona arqueológica donde se realizaron las excavaciones controladas de donde proceden los artefactos. Por los contextos en que se recuperaron, correspondientes a los rellenos constructivos y material de derrumbe, los artefactos de la muestra corresponden al periodo Clásico (100-900 d.C.), momento de mayor actividad constructiva y ocupacional dentro de las Estructuras 125 y 130 del Grupo F (Clark y Lee, 2018; Lowe et al., 1982). Los artefactos fueron analizados mediante la técnica de fluorescencia de rayos X en su modo portátil empleando un equipo marca Bruker modelo Tracer III-IV+ que consta de un tubo de Rh, un detector de Si y una ventanilla del detector de Be. Los parámetros establecidos para la medición de las muestras fueron los siguientes: (1) voltaje de 40 kV, (2) corriente de 25 amp, (3) tiempo de exposición de 200 s, (4) ambiente normal. Se utilizó un filtro de 12 mil Al/1 mil Ti/6 mil Cu, diseñado por el fabricante específicamente para la medición de obsidianas. Se utilizó un coeficiente empírico de fábrica (GL1) para la conversión de energía a composición química, el cual permitió determinar las concentraciones de 10 elementos (Mn, Fe, Zn, Ga, Th, Rb, Sr, Y, Zr, Nb).

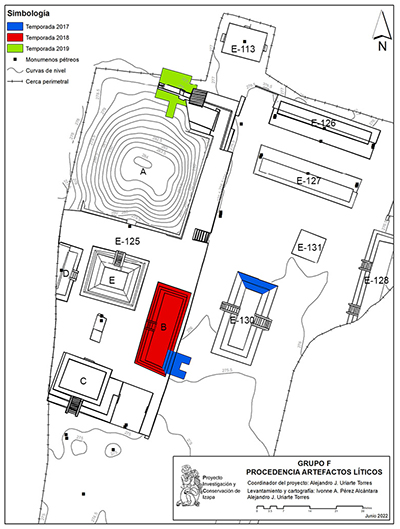Figura 4. Áreas de excavación de donde proceden los artefactos de obsidiana analizados.

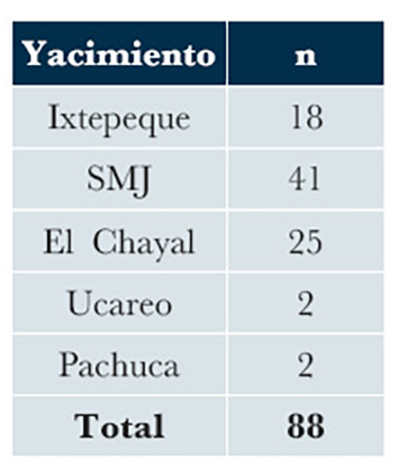
De acuerdo con el método aquí propuesto, se realizó una clasificación semi-supervisada usando el modelo de distribución MSPE de las n = 88 muestra de obsidiana recuperadas; como grupos de referencia se utilizaron los datos de los yacimientos de la Tabla 1. El resultado del modelo puede observarse en la Tabla 6, donde se apreciar que San Martín Jilotepeque es el yacimiento con mayor presencia, seguido de El Chayal y después de Ixtepeque, manteniendo un patrón de aprovisionamiento de materia prima similar al que venía dándose desde el periodo Preclásico terminal observado por el estudio de Mendelsohn (2017). Así mismo, se lograron detectar dos artefactos provenientes de Pachuca y dos de Ucareo. El BIC eligió el “EEEEV” (volumen igual, tamaño igual y orientación variable) con 5 componentes como el modelo que mejor se ajustaba a los datos. Con el resultado obtenido, puede observarse que los habitantes de Izapa tenían un acceso preferencial a los tres principales yacimientos de obsidiana de Guatemala, fuentes que aprovisionaron de materia prima a gran parte de los asentamientos del sureste mesoamericano desde el periodo Preclásico, incluyendo al Soconusco (Clark et al., 1989; Mendelsohn, 2018; Stark et al., 2016).

El Chayal, San Martín Jilotepeque e Ixtepeque fueron las tres fuentes de obsidiana más importantes de las tierras altas de Guatemala y cuya materia prima fue distribuida a través de largas redes comerciales de norte a oeste hacia la costa del Pacífico, Belice y las Tierras Bajas Mayas (Carr, 2015; Nazaroff et al., 2010), y hacia el sur hasta El Salvador, Honduras y Nicaragua (Sheets et al., 1990). El inicio de la explotación de las fuentes guatemaltecas comenzó en el período Preclásico medio (1000 a 400 a.C.), siendo San Martín Jilotepeque más representativo de este período (Brown et al., 2004). Desde el Preclásico tardío hasta el Clásico terminal (del 400 a.C. al 900 d.C.), El Chayal se convirtió en la fuente dominante, siendo eclipsado por Ixtepeque en el período posclásico (900-1500 d.C.) (Nazaroff et al., 2010). Los estudios de Mendelsohn (2017; 2018) coinciden con la presencia de artefactos procedentes de Jilotepeque y El Chayal; a diferencia de nuestros datos, la ausencia de materiales de Ixtepeque en el estudio de Mendelsohn (2017) probablemente se deba a que este yacimiento fue explotado mayormente durante el periodo Posclásico y la temporalidad de las piezas analizadas por ella se asociaba principalmente al período Preclásico terminal.

Tabla 6. Clasificación de los artefactos de obsidiana recolectados del sitio arqueológico de Izapa, Chiapas.

Por otro lado, aunque solamente con dos unidades de cada yacimiento, se ratifica la presencia de obsidiana del yacimiento de Sierra de Pachuca en Hidalgo y se adiciona la de Ucareo en Michoacán, lo que sugiere un cierto nivel de intercambio a larga distancia entre Izapa y el Centro de México para el periodo Clásico. Para este periodo, la explotación y/o distribución de materiales tanto de Sierra de Pachuca como de Ucareo están relacionados con el control e influencia teotihuacanas. En este sentido, cabe señalar las observaciones de Clark y Lee (2018), quienes describen una colección de joyería de obsidiana verde utilizada como parte del ajuar funerario de enterramientos localizados en el conjunto de la Estructura 125 durante las excavaciones de la NWAF en la década de 1960, esta presentó características de manufactura propias de Teotihuacán. Con base en lo anterior, estos autores propusieron que tales artefactos fueron elaborados en aquella urbe y adquiridos mediante intercambios entre miembros de las élites durante los periodos Clásico temprano y Clásico medio (200-600 d.C.), lo cual pudo ser también el caso de los materiales presentados en este trabajo.

4. Conclusiones

Durante décadas se ha tratado de resolver el problema de procedencia de materiales arqueológicos utilizando métodos de la estadística clásica o métodos exploratorios conocidos como métodos no-supervisados, como son los gráficos bidimensionales, el análisis de clústeres o el análisis de componentes principales. Sin embargo, se ha comprobado que estos métodos confunden los grupos, provocando traslapes y la dispersión de muestras que pertenecen a un mismo grupo pueden ser separados en varios grupos diferentes. Por otra parte, existen algunos estudios en donde se ha implementado la clasificación supervisada para determinar la procedencia, la cual implica el conocimiento a priori de las unidades experimentales. El inconveniente es que algunos de los modelos utilizados están restringidos por ciertos supuestos teóricos que no se satisfacen, como el de normalidad de las variables y la homogeneidad de varianzas en los grupos (para el caso del Análisis Discriminante) o el tamaño de muestra de los grupos de referencia (como es el caso de la Distancia de Mahalanobis). Si tales supuestos no son respetados, pueden ocasionar una asignación incorrecta de las unidades de muestra.

Por otro lado, la clasificación supervisada requiere de una gran cantidad de muestras etiquetadas para realizar el entrenamiento. No obstante, existen situaciones en donde es difícil disponer de un número suficiente de ejemplos para el entrenamiento. Los modelos mixtos gaussianos constituyen un método muy efectivo para agrupar y clasificar ciertos tipos de datos. Sin embargo, el modelo de mezcla gaussiana puede tener dificultades para acomodar grupos con colas pesadas o valores atípicos. Para evitar estos inconvenientes de los métodos tradicionales, en este artículo se propuso un método para determinar la procedencia de materiales arqueológicos usando un método de clasificación semi-supervisada, en la cual se predefine un conjunto de clases y se entrena al sistema mediante un conjunto de muestras etiquetadas cuyo origen se conoce con exactitud. Una vez entrenado el sistema, este es usado para clasificar automáticamente a un nuevo conjunto de datos cuyo origen se desconoce.

El modelo propuesto para hacer la asignación de las muestras a su clase (yacimiento) correspondiente es el de la distribución multivariante sesgada de potencia exponencial (MSPE). Este, al ser un modelo adaptado para manejar datos sesgados y simétricos, no se ve afectado por valores atípicos, ajustando el número óptimo de componentes de la mezcla. La ventaja de estos modelos es que pueden modelar simultáneamente una combinación de distribuciones platicúrticas, leptocúrticas y gaussianas (colas más delgadas, colas más anchas o colas más pesadas) con la asimetría. Como resultado, las distribuciones MSPE son más apropiadas para modelar datos heterogéneos con componentes de grupos no gaussianos. Para la estimación de los parámetros, se aplica un enfoque generalizado de maximización de expectativas (GEM) con pasos de maximización condicional. Además, el MSPE permite el ajuste simultáneo de una familia de 16 modelos de mezclas, reteniendo el modelo que mejor ajusta a los datos de un conjunto finito de modelos. Pare ello utiliza el Criterio de Información Bayesiano (BIC), cuya función es mitigar el riesgo de ajuste excesivo al introducir una penalización.

Para comprobar la efectividad del modelo, se realizó un experimento controlado utilizando una base de datos que contenía la concentración química de 16 yacimientos de obsidiana: 13 localizados en diversas regiones de México y 3 en Guatemala. En este ejercicio, se etiquetó sólo el 42% de las muestras y el resto se manejó como datos de procedencia desconocida. La asignación del método fue efectiva en el 100% de los casos. Como aplicación a datos arqueológicos, se tomó a los mismos 16 yacimientos como grupos de referencia para hacer la asignación de n = 88 muestras recuperadas del sitio arqueológico de Izapa, Chiapas. El método permitió asignar los materiales arqueológicos a cinco yacimientos, corroborando la importancia que desempeñaron las fuentes del altiplano guatemalteco en el aprovisionamiento de obsidiana para los habitantes de Izapa durante el periodo Clásico, pero también su participación en amplias redes de intercambio interregionales como se infiere de la identificación de fuentes del centro y occidente de México. A partir de los casos aquí presentados, puede concluirse que el método de clasificación semi-supervisada a través la familia MSPE demostró tener un rendimiento superior al de los métodos comúnmente utilizados en los estudios de procedencia.

Contribuciones de los autores

Conceptualización: López García, P. A., Argote Espino, D. L.; Análisis o adquisición de datos: López García, P. A., Argote Espino, D. L.; Desarrollo metodológico/técnico: López García, P. A., Cifuentes Nava, G.; Redacción del manuscrito original: López García, P. A., Argote Espino, D. L.; Redacción del manuscrito corregido y editado: López García, P. A., Argote Espino, D. L.; Diseño gráfico: Argote Espino, D. L., Uriarte Torres, A. J.; Trabajo de campo: Uriarte Torres, A. J., Pérez Alcántara, I. A.; Interpretación: Uriarte Torres, A. J., Pérez Alcántara, I. A., Argote Espino, D. L.

Financiamiento

Las excavaciones arqueológicas de las cuales provienen los materiales arqueológicos aquí analizados fueron realizadas mediante recursos financieros del Sistema Institucional de Proyectos del INAH procedentes del “Proyecto de Investigación y Conservación de Izapa”.

Agradecimientos

Agradecemos a Armando Macias y Carlos Andrés Hernández de la empresa RAISA (Radiación Aplicada a la Industria S.A. de C.V.) por proporcionarnos el espectrómetro de FRX. También agradecemos a los trabajadores técnico-manuales de las comunidades de Tuxtla Chico y Segunda Sección de Izapa que nos apoyaron en las actividades de excavación de la zona arqueológica.

Conflictos de interés

Los autores hacen constar que no existen conflictos de interés con otros autores, instituciones u otros terceros sobre el contenido (total o parcial) del artículo.

Editor a cargo

Avto Gogichaishvili

Referencias

Aitchison, J., 1986, The statistical analysis of compositional data: London, Chapman & Hall, 416 p.

Banfield, J.D., Raftery, A. E., 1993, Model-based Gaussian and non-Gaussian clustering: Biometrics, 49(3), 803-821. https://doi.org/10.2307/2532201

Baxter, M., Buck, C., 2000, Data handling and statistical analysis, in Ciliberto, E., Spoto, G. (eds.), Modern analytical methods in art and archaeology: New York, Wiley-Interscience, 681-746.

Baxter, M.J., Jackson, C.M., 2001, Variable selection in artefact compositional studies: Archaeometry, 43(2), 253-268. https://doi.org/10.1111/1475-4754.00017

Baxter, M.J., Beardah, C.C., Cool, H.E. M., Jackson, C.M., 2003, Compositional data analysis in archaeometry, en Compositional Data Analysis Workshop 2003: Girona, España, Universidat de Girona. https://core.ac.uk/display/132548242

Biernacki, C., Celeux, G., Govaert, G., 2003, Choosing starting values for the EM algorithm for getting the highest likelihood in multivariate Gaussian mixture models: Computational Statistics & Data Analysis, 41(3-4), 561-575. https://doi.org/10.1016/s0167-9473(02)00163-9

Braswell, G.E., Clark, J.E., Aoyama, K., McKillop, H.I., Glascock, M.D., 2000, Determining the geological provenance of obsidian artifacts from the Maya region: a test of the efficacy of visual sorting: Latin American Antiquity, 11(3), 269-282. https://doi.org/10.2307/972178

Brown, D.O., Dreiss, M.L., Hughes, R.E., 2004, Preclassic obsidian procurement and utilization at the maya site of Colha, Belize: Latin American Antiquity, 15(2), 222-240. https://doi.org/10.2307/4141555

Browne, R., Dang, J., Gallaugher, M.P., McNicholas, P., 2022, mixSPE - Mixtures of power exponential and skew power exponential distributions for use in model-based clustering and classification (en línea): CRAN package repository, R Foundation, actualizado 22 de octubre de 2022, disponible en <https://cran.r-project.org/web/packages/mixSPE/mixSPE.pdf>, consultado 16 de abril de 2023

Carr, S.P., 2015, Geochemical characterization of obsidian subsources in highland Guatemala: Pennsylvania, U.S.A., The Pennsylvania State University, Schreyer Honors College, Department of Anthropology, tesis de maestría, 100 p.

Charlton, M.F., Blakelock, E., Martinón-Torres, M., Young, T., 2012, Investigating the production provenance of iron artifacts with multivariate methods: Journal of Archaeological Science, 39 (7), 2280-2293. https://doi.org/10.1016/j.jas.2012.02.037

Clark, J.E., Lee, T.A., 2018, A touch of Teotihuacan at Izapa: the contents of two burials from Group F: Ancient Mesoamerica, 29(2), 265-288. https://doi.org/10.1017/s0956536118000147

Clark, J.E., Lee T.A., Salcedo, T., 1989, The distribution of obsidian, in Voorhies, B. (ed.), Ancient Trade and Tribute: Economies of the Soconusco Region of Mesoamerica: Salt Lake City, University of Utah Press, 268-284.

Cohen A.S., Pierce, D.E., 2018, Geochemical data from Angamuco, Michoacán, Mexico: Data in Brief, 23, 103633. https://doi.org/10.1016/j.dib.2018.12.071

Dang, U.J., 2014, Mixtures of power exponential distributions and topics in regression-based mixture models: Ontario, Canada, University of Guelph, tesis doctoral, 172 p.

Dang, U.J., Gallaugher, M.P.B., Browne, R.P., McNicholas, P.D., 2023, Model-based clustering and classification using mixtures of multivariate skewed power exponential distributions: Journal of Classification, 40, 145-167. https://doi.org/10.1007/s00357-022-09427-7

Dempster, A.P., Laird, N.M., Rubin, D.B., 1977, Maximum likelihood from incomplete data via the EM algorithm: Journal of the Royal Statistical Society: Series B (Methodological), 39(1), 1-22. https://doi.org/10.1111/j.2517-6161.1977.tb01600.x

Egozcue, J.J., Pawlowsky-Glahn, V., Mateu-Figueras, G., Barceló-Vidal, C., 2003, Isometric Logratio Transformations for Compositional Data Analysis: Mathematical Geology, 35, 279-300. https://doi.org/10.1023/A:1023818214614

Egozcue, J.J., Pawlowsky-Glahn, V., 2005, Groups of Parts and Their Balances in Compositional Data Analysis: Math Geol, 37, 795–828. https://doi.org/10.1007/s11004-005-7381-9

Egozcue, J. J., Pawlowsky-Glahn, V., 2011, Basic concepts and procedures, in Pawlowsky-Glahn, V., Buccianti, A. (eds.), Compositional Data Analysis Theory and Applications: London, John Wiley & Sons, 12-28. https://doi.org/10.1002/9781119976462.ch2

Egozcue, J. J., Pawlowsky-Glahn, V., 2016, Changing the Reference Measure in the Simplex and its Weighting Effects: Austrian Journal of Statistics, 45(4), 25–44. https://doi.org/10.17713/ajs.v45i4.126

Ferguson, J.R., 2012, , in Shugar, A., Mass, J. (eds.), Handheld XRF for art and archaeology: Leuven, Leuven University Press, 401-422.

Fop, M., Murphy, T.B., 2018, Variable selection methods for model-based clustering: Statistics Surveys, 12, 18-65. https://doi.org/10.1214/18-ss119

Franczak, B.C., Browne, R.P., McNicholas, P.D., 2014, Mixtures of shifted asymmetric Laplace distributions: IEEE Transactions on Pattern Analysis and Machine Intelligence, 36(6), 1149-1157. https://doi.org/10.1109/TPAMI.2013.216

García Gómez, V.H., 2018, Procedencia e intercambio de obsidiana en la Cuenca de México en el Holoceno medio (6000-4000 a.n.e.): el caso de San Gregorio Atlapulco, Xochimilco: México, Universidad Nacional Autónoma de México, Instituto de Investigaciones Antropológicas, tesis de maestría, 175 p.

Glascock, M.D., 1992, Characterization of archaeological ceramics at MURR by neutron activation analysis and multivariate statistics, in Neff, H. (ed.), Chemical characterization of ceramic pastes in archaeology: Madison, Prehistory Press, 11-26.

Glascock, M.D., 2010, Comparison and contrast between XRF and NAA: used for characterization of obsidian sources in Central Mexico, in Shackley, S. (ed.), X-ray fluorescence spectrometry (xrf) in geoarchaeology: New York, Springer, 161-192. https://doi.org/10.1007/978-1-4419-6886-9_8

Glascock, M.D., Neff, H., 2003, Neutron activation analysis and provenance research in archaeology: Measurement Science and Technology, 14(9), 1516-1526. https://doi.org/10.1088/0957-0233/14/9/304

Glascock, M.D., Braswell, G., Cobean, R., 1998, A systematic approach to obsidian source characterization, in Shackley, M. S. (ed.), Archaeological obsidian studies: method and theory. volume 3: New York, Plenum Press, 15-65.

Hall, M., 2004, Pottery production during the Late Jomon period, insights from the chemical analyses of Kasori B pottery: Journal of Archaeological Science, 31(10), 1439-1450. https://doi.org/10.1016/j.jas.2004.03.004

Hall, M., Minyaev, S., 2002, Chemical analyses of Xiong-nu pottery, a preliminary study of exchange and trade on the inner Asian steppes: Journal of Archaeological Science, 29(2), 135-144. https://doi.org/10.1006/jasc.2001.0699

Harbottle, G., 1982, Chemical characterization in archaeology, in Ericson, J., Earle, T. K. (eds.), Contexts for Prehistoric Exchange: New York, Academic Press, 13-51. https://doi.org/10.1016/B978-0-12-241580-7.50007-3

Hodge, M.G., Neff, H., Blackman, M. J., Minc, L.D., 1992, A compositional perspective on ceramic production in the Aztec empire, in Neff, H. (ed.), Chemical characterization of ceramic paste. Monographs in World Archaeology no. 7: Madison, Prehistory Press, 203-220.

Hron, K., Jelínková, M., Filzmoser, P., Kreuziger, R., Bednář, P., Barták, P., 2012, Statistical analysis of wines using a robust compositional biplot: Talanta, 90, 46-50. https://doi.org/10.1016/j.talanta.2011.12.060

Hughes, R.E., 1984, Obsidian studies in the Great Basin (No. 45): Berkeley: University of California, Berkeley, Dept. of Anthropology, Archaeological Research Facility, 231 p.

Hubert, L., Arabie, P., 1985, Comparing partitions: Journal of Classification, 2(1), 193-218. https://doi.org/10.1007/bf01908075

Kass, R.E., Raftery, A. E., 1995, Bayes factors: Journal of the American Statistical Association., 90(430), 773-795. https://doi.org/10.1080/01621459.1995.10476572

Korhonová, M., Hron, K., Klimcíková, D., Müller, L., Bednár, P., Barták, P., 2009, Coffee aroma-statistical analysis of compositional data: Talanta, 80(2), 710-715. https://doi.org/10.1016/j.talanta.2009.07.054

Kovarovic, K., Aiello, L.C., Cardini, A., Lockwood, Ch.A., 2011, Discriminant function analyses in archaeology: Are classification rates too good to be true?: Journal of Archaeological Science, 38(11), 3006-3018. https://doi.org/10.1016/j.jas.2011.06.028

Lopez-García, P., Argote, D.L., Beirnaert, C., 2019, Chemometric analysis of Mesoamerican obsidian sources: Quaternary International, 510, 100-118. https://doi.org/10.1016/j.quaint.2018.12.032

López-García, P.A., Vidal-Aldana, C.I., Gómez-Ambríz, E.A., Argote, D.L., 2021, The obsidian of la ferrería site: Local consumption and long-distance interactions in north and northwestern Mexico: Journal of Archaeological Science: Reports, 38, 103081. https://doi.org/10.1016/j.jasrep.2021.103081

López-García, P.A., Argote, D.L., 2023, Cluster analysis for the selection of potential discriminatory variables and the identification of subgroups in archaeometry: Journal of Archaeological Science: Reports, 49, 104022. https://doi.org/10.1016/j.jasrep.2023.104022

Lowe, G.W., Lee, T.A., Martínez, E., 1982, Izapa: an introduction to the ruins and monuments: Brigham Young University Papers of the New World Archaeological Foundation, 31, 349 p.

Mateu-Figueras, G., Martín-Fernandez, J.A., Pawlowsky-Glahn V., Barcelo-Vidal, C., 2003, El problema del análisis estadístico de datos composicionales, en Actas del 27 Congreso Nacional de Estadística e Investigación Operativa: Lleida, España, 480-488.

Mendelsohn, R.R., 2017, Resilience and interregional interaction at the early Mesoamerican city of Izapa: Formative to Classic period transition: Albany, New York, University at Albany, College of Arts & Sciences, Department of Anthropology, Tesis doctoral, 587 p.

Mendelsohn, R.R., 2018, Obsidian sourcing and dynamic trade patterns at Izapa, Chiapas, Mexico: 100 BCE–400 CE: Journal of Archaeological Science: Reports, 20, 634-646. https://doi.org/10.1016/j.jasrep.2018.06.002

Melnykov, V, 2010, Finite mixture models and model-based clustering: Statistics Surveys, 4, 80-116. https://doi.org/10.1214/09-SS053

Millhauser, J.K., Rodríguez-Alegría, E., Glascock, M.D., 2011, Testing the accuracy of portable X-ray fluorescence to study Aztec and Colonial obsidian supply at Xaltocan, Mexico: Journal of Archaeological Science, 38(11), 3141-3152. https://doi.org/10.1016/j.jas.2011.07.018

Moholy-Nagy, H., Meierhoff, J., Golitko, M., Kestle, C., 2013, An analysis of pXRF obsidian source attribution from Tikal, Guatemala: Latin American Antiquity, 24(1), 72-97. https://doi.org/10.7183/1045-6635.24.1.72

Morris, K., Punzo, A., McNicholas, P., Browne, R., 2019, Asymmetric clusters and outliers: Mixtures of multivariate contaminated shifted asymmetric Laplace distributions: Computational Statistics & Data Analysis, 132, 145-166. https://doi.org/10.1016/j.csda.2018.12.001

Nazaroff, A., Prufer, K., Drake, B., 2010, Assessing the applicability of portable X-ray fluorescence spectrometry for obsidian provenance research in the Maya lowlands: Journal of Archaeological Science, 37(4), 885-895. https://doi.org/10.1016/j.jas.2009.11.019

Pawlowsky-Glahn, V., Buccianti, A. (eds.), 2011, Compositional data analysis: theory and applications: London, John Wiley & Sons, 373 p.

Petřík, J., Nováček, K., Všianský, D., Al-Juboury, A., Slavíček, K., 2020, Islamic glazed pottery from Adiabene (Iraq, Kurdistan): multianalytical research into its technological development and provenance. Archaeological and Anthropological Sciences, 12(1), 1-25. https://doi.org/10.1007/s12520-019-01002-3

Pierce, D., 2015, Visual and geochemical analyses of obsidian source use at San Felipe Aztatán, Mexico: Journal of Anthropological Archaeology, 40, 266-279. https://doi.org/10.1016/j.jaa.2015.09.002

R Core Team, 2020, R: A language and environment for statistical computing (en línea): Vienna, Austria, R Foundation for Statistical Computing, disponible en <https://www.R-project.org/>, consultado 20 de abril de 2023.

Reimann, C., Filzmoser, P., 2000, Normal and lognormal data distribution in geochemistry: death of a myth. Consequences for the statistical treatment of geochemical and environmental data: Environmental Geology, 39(9), 1001–1014. https://doi.org/10.1007/s002549900081

Reimann, C., Filzmoser, P., Garret, R. G., 2002, Factor analysis applied to regional geochemical data: problems and possibilities: Applied Geochemistry, 17(3), 185-206. https://doi.org/10.1016/S0883-2927(01)00066-X

Resler, A., Yeshurun, R., Natalio, F., Raja, G. 2021, A deep-learning model for predictive archaeology and archaeological community detection: Humanities and Social Sciences Communications, 8, 295. https://doi.org/10.1057/s41599-021-00970-z

Rosenswig, R.M., Mendelsohn, R.R., 2016, Izapa and the Soconusco region, Mexico, in the first millenium A.D.: Latin American Antiquity, 27(3), 357-377. https://doi.org/10.1017/S1045663500015789

Shackley, M.S., 1988, Sources of archaeological obsidian in the southwest: an archaeological, petrological, and geochemical study: American Antiquity, 53(4), 752-772. https://doi.org/10.2307/281117

Shackley, M.S., 1994, Intersource and intrasource geochemical variability in two newly discovered archaeological obsidian sources in the southern Great Basin: Journal of California and Great Basin Anthropology, 16(1), 118-129. https://escholarship.org/uc/item/8p28x1p1

Schwarz, G., 1978, Estimating the dimension of a model: The Annals of Statistics, 6(2), 461-464. https://doi.org/10.1214/aos/1176344136

Sheets, P., Hirth, K., Lange, F., Stross, F., Asaro, F., Michel, H., 1990, Obsidian sources and elemental analysis of artifacts in southern Mesoamerica and the northern intermediate area: American Antiquity, 55(1), 144-158. https://doi.org/10.2307/281500

Stark, B.L., Boxt, M. A., Gasco, J., González Lauck, R.B., Hedgepeth Balkin, J.D., Joyce, A.A., King S.M., Knight, C.L.F., Kruger, R., Levine, M.N., Les, R.G., Mendelsohn, R., Navarro-Castillo, M., Neff, H., Ohnersorgen, M., Pool, C.A., Raab, L.M., Rosenswig, R.M., Venter, M., Voorhies, B., Workinger, A., 2016, Economic growth in Mesoamerica: obsidian consumption in the coastal lowlands: Journal of Anthropological Research, 41, 263-282. https://doi.org/10.1016/j.jaa.2016.01.008

Templ, M., Filzmoser, P., Reimann, C., 2008, Cluster analysis applied to regional geochemical data: problems and possibilities: Applied Geochemistry, 23(8), 2198-2213. https://doi.org/10.1016/j.apgeochem.2008.03.004

Tykot, R.H., 2016, Using nondestructive portable X-ray fluorescence spectrometers on stone, ceramics, metals, and other materials in museums: advantages and limitations: Applied Spectroscopy, 70(1), 42–56. https://doi.org/10.1177/0003702815616745

Uriarte, A.J., Pérez, I.A., 2018, Izapa, Chiapas: el impacto del crecimiento poblacional y los desafíos para su conservación: ARK Magazine, 6(21), 178-193.

APÉNDICE

Apéndice: Scripts para R

## script Model-based clustering and classification using mixtures

##of multivariate skewed power exponential distributions

library(mixSPE) ##Browne, R., Dang, U., Gallaugher, M and McNicholas, P. (2022)

rm(list = ls())

data2 <- read.csv(“File_X.csv”,header=T) ##

str(data2)

data2$index

membership <- as.numeric((data2[, “index”]))

membership

label <- membership

label

dat <- data.matrix(data2[, 1:9])

semisup_class_skewed = EMGr(data=dat, initialization=0, iModel=”EIIV”,

G=16, max.iter=500, epsilon=5e-3, label=label, modelSet=”all”,

skewness=TRUE, keepResults=TRUE, seedno=1, scale=FALSE)

table(membership,semisup_class_skewed$bestmod$map)

str(semisup_class_skewed)

semisup_class_skewed$bestmod$map

semisup_class_skewed$bestmod

semisup_class_skewed$BIC

Peer Reviewing under the responsibility of Universidad Nacional Autónoma de México.

This is an open access article under the CC BY-NC-SA license(https://creativecommons.org/licenses/by-nc-sa/4.0/)