Boletín de la Sociedad Geológica Mexicana Volumen 76, núm. 2, A150124, 2024 http://dx.doi.org/10.18268/BSGM2024v76n2a150124

Corrección de línea base semiautomática para espectroscopía infrarroja por transformada de Fourier (FTIR) para análisis arqueométricos

Semiautomatic baseline correction for Fourier transform infrared spectroscopy to archeometric analysis

Alan Nagaya¹, Oscar G. de Lucio^{1, *}, Laura López¹

¹ Laboratorio Nacional de Ciencias para la Investigación y Conservación del Patrimonio Cultural, Universidad Nacional Autónoma de México, Ciudad Universitaria, 04510 Coyoacán, CDMX, Mexico.

* Autor para correspondencia:(O. G. de Lucio) olucio@ciencias.unam.mx

Cómo citar este artículo:

Nagaya, A., de Lucio, O.G., López, L., 2024, Corrección de línea base semiautomática para espectroscopía infrarroja por transformada de Fourier (FTIR) para análisis arqueométricos, 76 (2), A150124. http://dx.doi.org/10.18268/BSGM2024v76n2a150124

Manuscrito recibido: 1° de noviembre de 2023; manuscrito corregido: 12 de enero de 2024; manuscrito aceptado: 13 de enero de 2024.

RESUMEN

La espectroscopía Infrarroja por Transformada de Fourier (FTIR) es una técnica ampliamente utilizada que provee información molecular de la muestra analizada, que es sensible al ambiente de análisis y cambios en este. Por ello cuando se adquiere el espectro de un material, es necesario considerar también el espectro de fondo, dado que es común que los parámetros experimentales se modifiquen, la línea base puede variar. Por ese motivo se propone un algoritmo semiautomático de corrección de la línea base para espectros obtenidos por la espectroscopía Infrarroja por Transformada de Fourier (FTIR). En el cual, se ajustan polinomios de Chebyshev de cuarto orden a puntos seleccionados por un criterio umbral. El algoritmo fue aplicado al análisis de mezclas de CaCO₃ y SiO₂ de concentraciones conocidas, mostrando que la información del espectro se preserva. Posteriormente se aplicó el método en la verificación de la cristalinidad de huesos calcinados obteniendo que el algoritmo considere la forma de las bandas. Preservando la información física de los espectros, y eliminando errores causados por el usuario. Además de considerar desplazamientos de las bandas.

Palabras clave: FTIR, línea base, polinomios de Chebyshev, arqueometría.

ABSTRACT

Fourier transform infrared spectroscopy (FTIR) is a widely used technique that provides molecular information about the analyzed sample, which is sensitive to the analysis environment and changes in it. Therefore, when the spectrum of a material is acquired, the background must be taken into account, since it is common for the experimental parameters to be modified, the baseline varies as well. For this reason, a semi-automatic baseline correction algorithm is proposed for spectra obtained by Fourier Transform Infrared (FTIR) Spectroscopy. In which, fourth-order Chebyshev polynomials are fitted to points selected by a threshold criterion. The algorithm was applied to the analysis of CaCO₃ y SiO₂ mixtures, for known concentrations, showing that spectrum information is preserved. On the other hand, the method was applied to verify the crystallinity of calcined bones, obtaining that the algorithm considers the shape of the bands. Preserving the physical information of the spectra and eliminating user errors. In addition to considering for band displacements.

Keywords: FTIR, baseline, Chebyshev polynomies, archeometry.

1. Introducción

En la espectroscopía infrarroja se estudia la interacción de la radiación infrarroja (IR, por sus siglas en inglés) con la materia. La IR es invisible al ojo humano y está dividida en tres regiones: infrarrojo cercano (NIRS, por sus siglas en inglés), que comprende los números de onda 14000 cm^-1 - 4000 cm^-1; infrarrojo medio (MIRS, por sus siglas en inglés), que comprende los números de onda 4000 cm^-1 - 400 cm^-1; e infrarrojo lejano (FIRS, por sus siglas en inglés), que comprende los números de onda 400 cm^-1 - 10 cm^-1 (Theophanides, 2012).

La energía de la radiación IR no es lo suficientemente energética para excitar electrones. Sin embargo, puede interactuar con los átomos que conforman las moléculas, causando que los enlaces químicos de estas vibren de distintas formas. En este proceso es cuantizado, por lo que, la molécula sólo interactúa con ciertos números de onda, que corresponden a sus modos naturales de vibración (Khan et. al.,2018).

Una de las espectroscopías IR más extendidas actualmente es la Espectroscopía Infrarroja por Transformada de Fourier (FTIR, por sus siglas en inglés). El sistema óptico del espectrómetro está compuesto por la fuente de radiación, un interferómetro y un detector. Inicialmente, se adquiere un interferograma, que es procesado mediante la Transformada de Fourier, procedimiento que le da nombre a la técnica. Comúnmente, el espectro obtenido por esta técnica pertenece a la región MIRS. Las principales ventajas de su uso son que: provee una medición precisa que no requiere de calibración externa; el proceso de captura es rápido y sensible; tiene un mayor rendimiento óptico; y su mecanismo es simple ya que solo tiene una parte móvil: el interferómetro (Dutta, 2017; Mohamed et al., 2017).

Las tres características principales de las bandas en un espectro FTIR son frecuencia, forma e intensidad. La frecuencia indica la posición en la que los vemos en el espectro, si las bandas están en el intervalo 4000 cm^-1 - 1600 cm^-1, estas pertenecen a la región de grupos funcionales y nos dan información de la presencia de grupos funcionales presentes en el material. El intervalo 1600 cm^-1 - 400 cm^-1, es conocido como región de huellas dactilares, donde al ser cada material único en su composición y en su arreglo atómico, no hay dos materiales que tengan el mismo espectro en este intervalo (Derrick et al., 1999; Dutta, 2017).

La forma de las bandas nos indica la pureza del material, grupos funcionales y características del arreglo cristalino. Todas las bandas de absorción de moléculas puras son simétricas siguiendo una distribución normal. Cambios en alguna característica de esta distribución, como ensanchamiento de un lado de la curva, indica la superposición de dos (o más) bandas, así mismo, la presencia de bandas asimétricas puede indicar alguna modificación del material. El grosor de las bandas puede verse modificado por la interacción intermolecular e intramolecular, y la presencia de bandas dobles son causadas por efectos de red cristalina (Derrick et al., 1999).

La intensidad de las bandas está regida por la ecuación de Beer-Lambert (Ecuación 1), donde A(ν_i) es la absorbancia en el número de onda i, donde T(ν_i) es la transmitancia en el número de onda i, ε(ν_i) es el coeficiente de absorción molar en el número de onda i, c es la concentración en M=mol/L y l la longitud de camino óptico que atraviesa. Por lo tanto, la intensidad de las bandas está relacionada al momento del momento dipolar de la vibración (coeficiente de absorción molar) y la cantidad de material (concentración) (Bosch Reig et al., 1999; Derrick et al., 1999).

(1)

La técnica FTIR es sensible a los gases presentes en el ambiente de medición. Por ello cuando se adquiere el espectro de un material, primero se debe de obtener el espectro de fondo. El espectro de fondo es la distribución de intensidades de la fuente en el medio de análisis. Una vez obtenido el espectro de fondo, se puede medir la muestra, donde la transmitancia, es el cociente del espectro del material entre el espectro de fondo. Si el sistema óptico se mantiene consistente durante la medición del espectro del material y el espectro de fondo, la línea base obtenida en la región de no-absorción debería de ser 1, en el caso de la transmitancia y 0, en el caso de la absorbancia, sin embargo, es común que los parámetros se modifiquen debido a distintos factores. Cambios en la temperatura de la fuente, inclinación de los espejos del interferómetro, cambio en la modulación del interferómetro, cambios en la longitud de onda del láser, falta de la señal de interferencia en el muestreo (Zhang et al., 2022).

Debido a estas modificaciones es necesario corregir la línea base. El método de corrección de línea base más sencillo es el tangencial, como el que se ha usado en las investigaciones de Ortiz Ruiz et al. (2023) y Weiner et al. (2015). Sin embargo, este método carece de reproductibilidad y solo se puede aplicar localmente debido a que puede amplificar el ruido (Yu et al., 2013). Se han propuesto métodos automatizados de corrección, como el método de transformada de ondas pequeñas (wavelets) (Bertinetto y Vuorinen, 2014; Liu et al., 2019), mínimos cuadrados penalizados (Zhang et al., 2020), métodos polinómicos (Gan et al., 2006; Shen et al., 2018).

Una función polinómica que ha sido utilizada en el análisis de señales son los polinomios de Chebyshev, definidos por la Ecuación 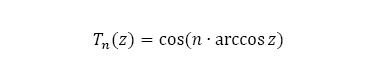2,

(2)

donde el conjunto Tn forma un conjunto ortogonal respecto a la función de peso w(z)=(1-z²)^-1/2 en el dominio |z|≤1, por lo que podemos usarlas como un subconjunto de estas para aproximar una función (Capozziello et al., 2018). Ajustes realizados con estas funciones han sido utilizados en el análisis de señales (Lázaro Castillo et al., 2009), en aproximaciones cosmográficas (Capozziello et al., 2018) y en el modelado de fondos de patrones de difracción, como se realiza en el software GSAS II (Toby y Von Dreele, 2013).

El propósito de este trabajo es presentar un algoritmo semiautomático de corrección de línea base, que puede ser aplicable a análisis cuantitativos de muestras pertenecientes al patrimonio cultural. El algoritmo propuesto selecciona puntos del espectro a los que se les aplica un ajuste de Chebyshev de manera local. Se verificó la reproducibilidad del método con mezclas de distintos porcentajes de los minerales cuarzo (SiO₂) y calcita (CaCO₃), posteriormente se aplicó a muestras de huesos calcinados de manera controlada.

2. Materiales y Métodos

2.1. Algoritmo

La Figura 1 describe brevemente el algoritmo propuesto. El espectro FTIR se analiza en absorbancia, y es tratado como un conjunto indexado i= {0, 1, 2, …} donde {yi} corresponde las absorbancias y tiene asociado un elemento {xi} a los números de onda. Haciendo uso del criterio de la primera y segunda derivada se encuentran los conjuntos de máximos locales {yj} y mínimos locales {yk}.

Definimos el Umbral (threshold) según la Ecuación 3, donde c es una constante definida por el usuario, que corresponde a un porcentaje por lo que 0<c<1.

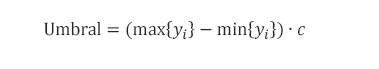(3)

El conjunto de puntos que conforma la línea base y_LBm será igual a los mínimos que cumplan con la condición, descrita en la Ecuación 3, donde y_j y y_j+1 son los máximos próximos a y_k, de número de onda menor y mayor respectivamente. La condición de Umbral, Ecuación 4, se impone para descartar la presencia de dobletes, la primera condición se cumple para todas aquellas señales que pertenecen a secciones del espectro que son ruido, con la segunda condición seleccionamos los mínimos entre bandas del espectro.

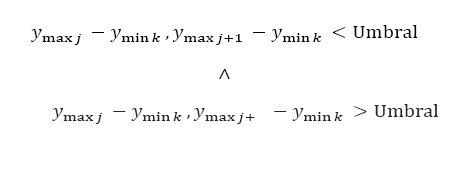(4)

Por último, discriminamos en grupos yn_LBm para ajustar un polinomio de Chebyshev de orden 4 según la condición y_LBm∈yⁿ_LB si |x_LBm-1-x_LBm|<100, si la condición no se cumple, se crea el grupo yⁿ⁺¹_LB empezando en m’=m_max+1. Las regiones no ajustadas mediante polinomios de Chebyshev se unen entre sí por una línea recta calculada con los extremos de los grupos yⁿ_LB.

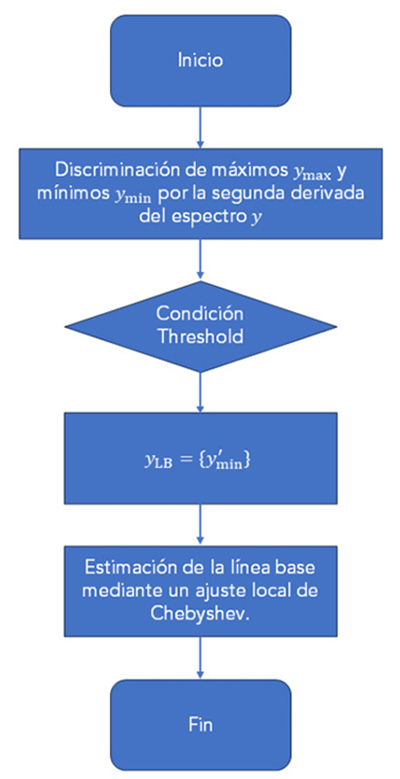Figura 1. Diagrama de flujo del algoritmo propuesto.

2.2. Adquisición de datos

Los espectros FTIR se adquirieron con el espectrómetro compacto Bruker Alpha II usando el módulo ATR. El espectrómetro cuenta con una fuente de radiación infrarroja CenterGlow y un láser de diodo. Utiliza un interferómetro de esquinas de cubo RockSolid y un detector de temperatura controlada DLaTGS, que para un divisor de haz de KBr, tiene un rango de 350 cm^-1 - 8000 cm^-1. El módulo de ATR utilizado cuenta con un cristal ATR de diamante con un ángulo de incidencia de 45°.

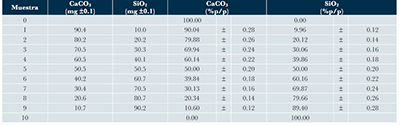
Tabla 1.  Masas y concentraciones de las mezclas de CaCO3 y SiO2.

Los espectros se obtuvieron en un rango del infrarrojo medio 400 cm^-1 - 4000 cm^-1, con una resolución de 4 cm^-1, promediando 32 escaneos. Cerciorándose que la muestra cubriera en su totalidad el cristal ATR. El equipo es capaz de analizar el espectro con micro muestras, sin embargo, las absorbancias reportadas son pequeñas. En este trabajo, deseamos cuantificar las muestras, por lo que quisimos la mayor absorbancia posible del material.2.3. Análisis de mezclas

Se prepararon 9 mezclas con distintas concentraciones de porcentaje peso a peso de CaCO₃ y SiO₂, la Tabla 1 resume las concentraciones usadas. Como reactivo de CaCO₃, se utilizó carbonato de calcio sintético Sigma Aldrich C4830. El espectro FTIR de este reactivo (Figura 2a) indica que el polimorfo de CaCO₃ analizado es calcita, debido a la aparición de los modos de vibración ν₃ en la posición 1393.14 cm^-1 ν₂ en la posición 871.74 cm^-1 y ν₄ en la posición 711.00 cm^-1 y no presentar un doblete; la presencia de los modos combinados ν₁+ν₄ y ν₁+ν₃; y la ausencia del modo de vibración ν₁ (Xu y Poduska, 2014). El material no presenta grupos funcionales, ni bandas adicionales, lo indica la alta pureza del reactivo.

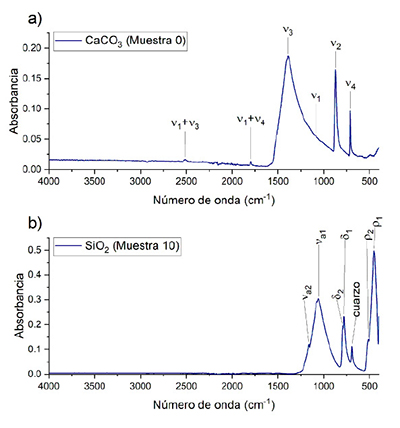Figura 2. Espectros antes de la corrección de la línea base de la Muestra 0 y la Muestra 10 con las bandas señaladas.

Como reactivo de SiO₂, se utilizó cuarzo de origen geológico. El espectro FTIR de este reactivo (Figura 2b) presenta los modos de vibración: estiramiento antisimétrico (ν_a) Si-O-Si en la posición 1162.32 cm^-1 y 1057.22 cm^-1; flexión antisimétrica dentro del plano (δ) Si-O-Si en la posición 795.49 cm^-1 y 776.94 cm^-1, flexión dentro del plano simétrica (ρ) Si-O-Si en la posición 515.21 cm^-1 y 451.33 cm^-1, y la banda relacionada a la estructura cristalina en la posición 694.51 cm^-1, en este caso cuarzo (Sharokh Abadi et al., 2015). El material no presenta grupos funcionales, ni bandas adicionales, lo indica la alta pureza del reactivo.

La Ecuación 1 la podemos reescribir en términos del porcentaje peso en peso de las especies de interés, Ecuación 5, donde w% es el porcentaje peso en peso, ρ es la densidad del reactivo y M es la masa molar del material (Chen et al., 201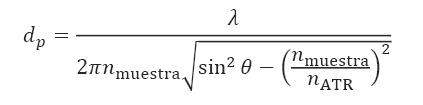5).

(5)

En el caso de la espectroscopía FTIR por ATR, la Ecuación 5 debe de modificarse l por la distancia de penetración d_p de la onda evanescente en el material, la distancia de penetración está dada por la Ecuación 6, donde λ es la longitud de onda, θ es el ángulo de incidencia del haz en el cristal ATR y n son los índices de refracción (Bradley, 2018).

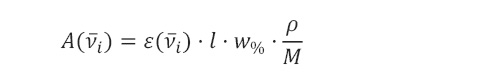(6)

Para las mezclas, la absorbancia resultante es igual a la suma aritmética de las absorbancias que componen la mezcla. Considerando que en el número de onda ν_i la absorbancia del componente i es mayor que cero, y la absorbancia del componente j es cero, y que en el número de onda ν_j la absorbancia del componente j es mayor que cero, y la absorbancia del componente i es cero. Así introduciendo la Ecuación 6 en la Ecuación 5, tenemos que el cociente entre las absorbancias es la Ecuación 7, donde podemos simplificar todas las constantes.

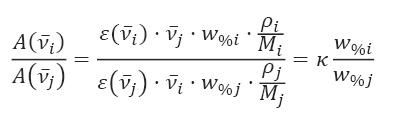(7)

Si la elección de línea base fuera de manera correcta calcularemos dos cocientes, consideraremos como ν_i los modos de vibración ν₂ y ν₄, como ν_j las flexiones antisimétricas dentro del plano δ₂ y δ₁, respectivamente. Así mismo obtenemos los cocientes de un espectro calculado con las absorbancias establecidas en las Muestra 0 y Muestra 10 siguiendo la ley de Beer-Lambert (Ecuación 1).

2.4. Tratamiento térmico de Huesos

La espectroscopía FTIR ha sido una herramienta que ha permitido a los arqueólogos documentar y analizar los usos del fuego por la humanidad. En el análisis de huesos las principales investigaciones realizadas con la técnica ayudan a identificar la diagénesis y temperaturas de cocción (Monnier, 2018). En los trabajos pioneros, Stiner et al. (1995) y Weiner y Bar-Yosef (1990), relacionaron el grado de cristalinidad de los huesos con el splitting factor (Ecuación 8) del modo de vibración dentro del plano antisimétrico (ν₄) del grupo fosfato (PO₄) (Figura 3), mostrando que son directamente proporcionales. El proceso térmico aplicado a los huesos hace que, la estructura cristalina de los mismos se ordene, teniendo tamaños de grano relativos y una cristalinidad mayor conforme la temperatura del proceso aumenta.

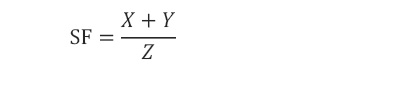(8)

Para construir una curva de calibración, se eligieron huesos de cerdo por las altas similitudes con los huesos humanos (Wang et al., 2019), estos se calcinaron durante cuatro horas a diez temperaturas distintas, desde los 200°C hasta los 1100°C, con pasos de 100°C. Los espectros se analizaron aplicando el algoritmo de línea base propuesto, con el fin de hacer medidas reproducibles en experimentos posteriores.

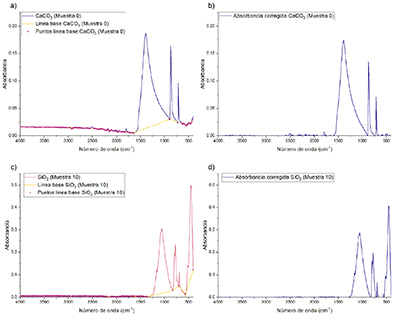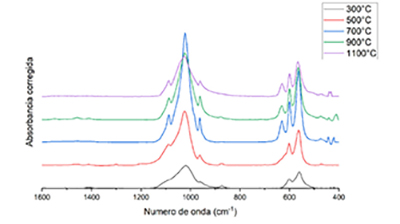
Figura 3. Espectros FTIR de huesos de cerdo calcinados a distintas temperaturas. Modos de vibración dentro del plano antisimético X=601.77 cm-1, Y=560.55 cm-1, Z=589.40 cm-1.

3. Resultados

3.1. Aplicación de la línea base

La Figura 4a y la Figura 4c, muestran los puntos y la línea base calculada que se seleccionaron con los criterios de Umbral para la línea base y el ajuste de línea base realizado de la Muestra 0 y la Muestra 10 respectivamente. La Figura 4b y la Figura 4d, muestran el espectro de absorbancia corregido.

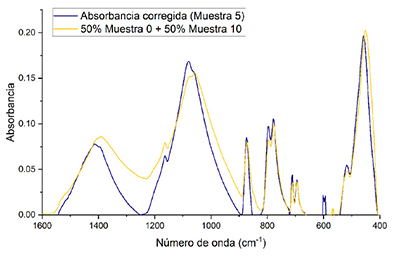Figura 4. Comparación de los espectros antes y después de la corrección de la línea base. a) Espectro de la Muestra 0 con los puntos de ajuste señalados y la línea base calculada. b) Espectro de la muestra 0 con la corrección de línea base. c) Espectro de la Muestra 10 con los puntos de ajuste señalados y la línea base calculada. d) Espectro de la muestra 10 con la corrección de línea base.

Dado que la absorbancia de una mezcla es la suma aritmética de las absorbancias. Siguiendo la Ecuación 5, la Figura 5 compara el espectro experimental de la muestra 5 corregido con un espectro calculado sumando el 50% de la absorbancia corregida de la Muestra 0 y 50% de la absorbancia corregida de la Muestra 10.

Figura 5. Comparación entre el espectro experimental de la Muestra 5 y el espectro calculado considerando una contribución del 50% de la Muestra 0 y 50% de la Muestra 10.

3.2. Análisis de Mezclas

La Figura 6, compara los resultados del cociente de absorbancias contra el cociente de porcentajes obtenidos de manera experimental y de manera calculada con las absorbancias corregidas para los dos cocientes. La línea recta se ajustó a los datos calculados y se presentan en escala logarítmica ambos ejes para una mejor lectura de los cocientes cercanos a cero. El ajuste lineal de los datos experimentales A(ν₄)/A(δ₂) presenta un valor R²=0.96 mientras que el A(ν₂)/A(δ₁) presenta un valor R²=0.95, para los datos calculados ambos tienen un valor R²=0.99, demostrando la relación lineal entre el cociente de concentraciones y el cociente de las absorbancias en los números de onda elegidos. Las constantes κ, para los datos A(ν₄)/A(δ₂) son κ_exp=0.61±0.05 y κ_cal =0.64±0.02. Así mismo, las constantes κ, para los datos A(ν₂)/A(δ₁) son κ_exp=0.36±0.02 y κ_cal =0.31±0.01.

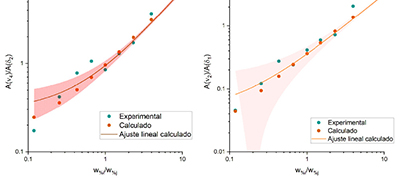Figura 6. a) Gráfica A(v4)/A(v2) vs w%i/w%j con el ajuste lineal de los datos calculados y la banda de confidencia del 95%. a) Gráfica A(v2)/A(v1) vs w%i/w%j con el ajuste lineal de los datos calculados y la banda de confidencia del 95%.

3.3. Tratamiento térmico de Huesos

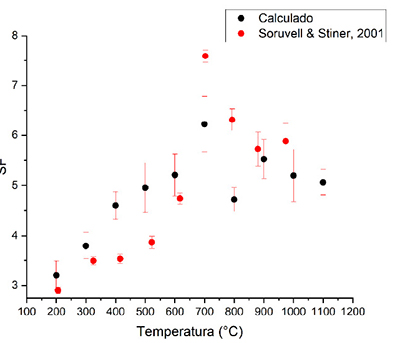
La Figura 7, muestra los espectros de los huesos después de la corrección de la línea base, destacando que el método no incluyó los mínimos del doblete (o triplete, en el caso de altas temperaturas) del grupo fosfato. La Figura 8, presenta la relación entre los valores SF de los espectros ajustados para cada temperatura de calcinación siguiendo la Ecuación 8, así como una comparación con los valores SF reportados en Surovell y Stiner (2001), en donde reproducimos el incremento del SF hasta 700°C y la caída posterior (Ellingham et al., 2015). Este comportamiento irregular coincide con la aparición de una banda adicional en el doblete, hacia 630 cm^-1. Esta banda modifica el comportamiento del doblete analizado, además de los puntos seleccionados por el umbral para la corrección de la línea base.

Figura 7. Corrección de línea base para los espectros de huesos a distintas temperaturas

4. Discusión

El método pudo aplicarse con una condición de umbral de manera global, con las Muestras 0 y 10, que son los reactivos sin mezclar; y las Muestras 3, 4, 5, 6 y 7, donde la suma de las absorbancias se vuelve significativa para ambos reactivos. Para las Muestras 1, 2, 8 y 9, por la alta concentración de un reactivo respecto a otro, la condición de umbral no se pudo aplicar de manera global, existían problemas en la región 700 cm^-1-900 cm^-1, debido a que las bandas del reactivo minoritario podían ser consideradas como dobletes por la condición de umbral y no reproducía los resultados esperados, por lo que se aplicó un umbral de manera local en esa región.

El método aplicado a las Muestra 0, logra preservar las bandas identificadas de la calcita, incluyendo los modos ν₁+ν₄ y ν₁+ν₃ (Figura 4b). Así mismo, al aplicarlo a la Muestra 10 (Figura 4d), observamos la aparición de una banda adicional en la región entre 500 cm^-1-700cm^-1, debido a que la línea base ajustada reporta valores negativos, debido a la poca densidad de puntos de línea base de la región.

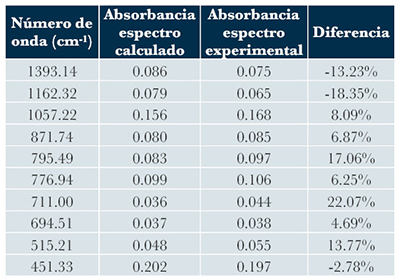
La comparación entre los espectros experimentales contra los calculados mediante la suma aritmética de las absorbancias de los reactivos sin mezclar (Figura 5) reproduce de manera adecuada las intensidades de las absorbancias. La Tabla 2 muestra que la mayor diferencia porcentual entre los espectros se presenta en el número de onda 711 cm^-1, pero es la banda con la menor absorbancia. Pese a que se preserven las intensidades, debido a la definición del umbral, la superposición de las bandas es considerada como un cero. Por lo que el espectro corregido no reproduce visualmente el comportamiento de la mezcla, pero sí la información física, como lo muestran la similitud de las constantes κ_exp y κ_cal.

Tabla 2. Diferencias porcentuales de las absorbancias experimentales respecto a las calculadas para el espectro de la Muestra 5.

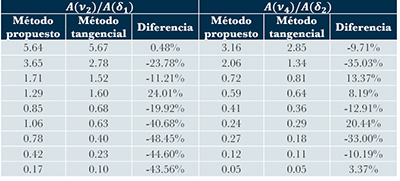
En la Tabla 3 se comparan los datos del cociente para ambos casos obtenidos por el método propuesto y el método tangencial, la metodología común en el análisis de espectros FTIR pertenecientes al patrimonio cultural, encontrando diferencias de más del 10%, en la mayoría de los casos, por lo que no podemos relacionar las constantes obtenidas en la curva de calibración por el método propuesto y el método tangencial, debido a que este último no considera los puntos vecinos.

Tabla 3. Comparación entre los cocientes por el método propuesto y el método tangencial.

Las diferencias presentadas en la curva de calibración del tratamiento térmico en huesos respecto a lo reportado por Surovell y Stiner (2001) (Figura 8), se deben a varias razones, la primera es la correlación entre el método tangencial y el método propuesto, pese a lo anterior, se preserva el comportamiento ascendente de la curva hasta los 700°C y el decaimiento posterior (Ellingham et al., 2015), además de que en la mayoría de los casos los puntos reportados respecto a los que se obtuvieron están dentro de la incertidumbre.

5. Conclusiones

El algoritmo aquí propuesto para la corrección de la línea base provee la información física en el análisis cuantitativo de espectros FTIR, además de la referencia visual del mismo. Logra preservar la información física de estos y reporta de manera correcta las absorbancias de las muestras analizadas. Debido al procedimiento de selección de los puntos que conformarán la línea base, se eliminan errores de posición causados por el usuario. Adicionalmente, considera desplazamientos de las bandas provocados por el sistema óptico o por la aparición de bandas, seleccionando los puntos adecuados en cada análisis. La aproximación mediante polinomios de Chebyshev permite modelar la línea base sin importar la contribución del fondo en el espectro.

Las principales áreas de oportunidad para la aplicación del algoritmo son para la discriminación de dobletes y para la superposición de bandas anchas que corresponden a la mezcla de sustancias. Ya que, con la propuesta de umbral, no logra discriminar las propiedades físicas del espectro, sólo se establece matemáticamente. Así mismo, la línea base reportada carece de significado físico y no corresponde directamente a la molécula analizada.

El algoritmo necesita del conocimiento del usuario de la molécula analizada. Sobre todo, identificar previamente las regiones donde hay dobletes para poder distinguir que los mínimos locales de esos dobletes no sean seleccionados como parte de la línea base, lo que conlleva a una correcta elección de un umbral, que no necesariamente puede aplicarse manera global en el espectro, siendo esta la única intervención del usuario en el análisis del espectro, haciendo que este algoritmo sea semiautomático, permitiendo así el análisis de una gran cantidad de datos. Además de que bajo condiciones similares el valor c del Umbral (Ecuación 3) debe de ser el mismo, lo que permite la reproductibilidad del método.

Contribuciones de los autores

Conceptualización: Nagaya, A.; Análisis o adquisición de datos: de Lucio, O.G., Nagaya, A., López, L.; Desarrollo metodológico/técnico: de Lucio, O.G., Nagaya, A.; Redacción del manuscrito original: de Lucio, O.G., Nagaya, A.; Redacción del manuscrito corregido y editado: de Lucio, O.G., Nagaya, A.; Diseño gráfico: de Lucio, O.G., Nagaya, A.; Interpretación: de Lucio, O.G., Nagaya, A.; Financiamiento: de Lucio, O.G.; Dirección y Administración de proyecto: de Lucio, O.G.

Financiamiento

Este trabajo fue financiado por el proyecto CONAHCYT CF 2019 No. 731762; y los proyectos CONAHCYT LN293904, LN 299076, LN314846, LN315853. Así como por los proyectos DGAPA-PAPIIT IN101920, IN113321, IN108521, IG100424.

Agradecimientos

Los autores agradecen el apoyo del Laboratorio Nacional de Ciencias para la Investigación y Conservación del Patrimonio Cultural (LANCIC-IF), que permitió realizar todo el trabajo experimental, sin el cual no habría sido posible esta investigación.

Conflictos de interés

Los autores hacen constar que no existen conflictos de interés con otros autores, instituciones u otros terceros sobre el contenido (total o en parte) del artículo.

Editor a cargo

Avto Goguitchaichvili.

Referencias

Bertinetto, C.G., Vuorinen, T., 2014, Automatic Baseline Recognition for the Correction of Large Sets of Spectra Using Continuous Wavelet Transform and Iterative Fitting: Applied Spectroscopy, 62 (2), 155-164. https://doi.org/10.1366/13-07018

Bosch-Reig, F., Gimeno-Adelantado, J.V., Peris-Martínez, V., Moya-Moreno, M.C., Domènech-Carbó, M.T., 1999, FT-IR quantitative analysis of solvent mixtures by the constant ratio method: Journal of Molecular Structure, 480-481, 529-534. https://doi.org/10.1016/S0022-2860(98)00919-3

Bradley, M., 2018, Pathleght Considerations With ATR Sampling in FTIR (en línea): Labcompare, disponible en: <https://www.labcompare.com/10-Featured-Articles/352695-Pathlength-Considerations-With-ATR-Sampling-in-FTIR/#:~:text=When%20IR%20light%20passes%20through,light%20transmitted%20through%20the%20sample>

Capozziello, S., D’Agostino, R., Luongo, O., 2018, Cosmographic analysis with Chebyshev polynomials: Monthly Notices of the Royal Astronomical Society, 476(3), 3924-3938. https://doi.org/10.1093/mnras/sty422

Chen, Y., Zou, C., Mastalerz, M., Hu, S., Casaway, C., Tao, X., 2015, Applications of Micro-Fourier Transform Infrared Spectroscopy (FTIR) in the Geological Sciences - A Review: International Journal of Molecular Sciences, 16(12), 30223-30250. https://doi.org/10.3390/ijms161226227

Derrick, M.R., Stulik, D., Landry, J.M., 1999, Spectral Interpretation, in Infrared Spectroscopy in Conservation Science: Los Angeles, The Getty Conservation Institute, 82-171.

Dutta, A., 2017, Fourier Transform Infrared Spectroscopy, in Thomas, S., Thomas, R., Zachariah, A.K., Kumar Mishra, R. (eds.), Spectroscopy methods for nanomaterials characterization: Philadelphia, Elsevier, 73-92.

Ellingham, S.T., Thompson, T.J., Islam, M., Gillian, T., 2015, Estimating temperature exposure of burnt bone - A methodological review: Science and Justice, 55(3), 181-188. https://doi.org/10.1016/j.scijus.2014.12.002

Gan, F., Ruan, G., Mo, J., 2006, Baseline correction by improved iterative polynomial fitting with automatic threshold: Chemometrics and intelligent laboratory systems, 82(1-2), 59-65. https://doi.org/10.1016/j.chemolab.2005.08.009

Khan, S.A., Khan, S.B., Khan, L.U., Farooq, A., Akhtar, K., Asiri, A.M., 2018, Fourier Transform Infrared Spectroscopy: Fundamentals and Application in Functional Groups and Nanomaterial Characterization, in Sharma, S. (ed.), Handbook of Materials Characterization: Cham, Switzerland, Springer, 317-344. https://doi.org/10.1007/978-3-319-92955-2_9

Lázaro-Castillo, I.I., Anzurez-Marín, J., Pineda-García, G., 2009, Aplicación de los Polinomios de Chebyshev al Análisis de Redes Eléctricas: Conciencia Tecnológica, 38, 11-17.

Liu, T., Liu, H., Zhang, Z., Liu, S, 2019, Efficient blind signal reconstruction with wavelet transforms regularization for educational robot infrared vision sensing: IEEE/ASME Transactions on Mechatronics, 24(1), 384-394. https://doi.org/10.1109/TMECH.2018.2870056

Mohamed, M.A., Jaafar, J., Ismail, A.F., Othman, M.H., Rahman, M.A., 2017, Fourier Transform Infrared (FTIR) Spectroscopy, in Hilal, N., Ismail, A.F., Matsuura, T., Oatley-Radcliffe, D. (eds.), Membrane Characterization: Londres, Elsevier, 3-29.

Monnier, G.F., 2018, A review of infrared spectroscopy in microarcheology: Methods, applications, and recent trends: Journal of Archeology Science Reports, 18, 806-823. https://doi.org/10.1016/j.jasrep.2017.12.029

Ortiz-Ruiz, S., de Lucio, O.G., Mitrani-Viggiano, A., Perez-Castellanos, N.A., Ruvalcaba-Sil, J. L., Barba-Pingarrón, L., Goguitchaichvili, A., 2023, Mayan Fire: Calibration curve for the determination of heating temperatures of limestone, lime and related materials by FTIIR measurements: Journal of Archeological Science Reports, 49, 103966. https://doi.org/10.1016/j.jasrep.2023.103966

Sharokh-Abadi, M.H., Delbari, A., Fakoor, Z., Baedi, J., 2015, Effects of Anneling Temperature on Infrared Spectra of SiO2 Extracted From Rce Husk: Journal of Ceramic Science and Technology, 06(1), 41-46.

Shen, X., Xu, L., Ye, S., Hu, R., Jin, L., Xu, H., Liu, W., 2018, Automatic baseline correction method for the open-path Fourier transform infrared spectra by using simple iterative averaging: Optics Express, 26(10), A609-A614. https://doi.org/10.1364/OE.26.00A609

Stiner, M.C., Kuhn, S.L., Weiner, S., Bar-Yosef, O., 1995, Differential Burning, Recrystallization, and Fragmentation of Archeological Bone: Journal of Archeological Science, 22(2), 223-237. https://doi.org/10.1006/jasc.1995.0024

Surovell, T.A., Stiner, M.C., 2001, Standardizing Infra-red Measures of Bone Mineral Crystallinity: an Experimental Approach: Journal of Archeological Science, 28(6), 633-642. https://doi.org/10.1006/jasc.2000.0633

Theophanides, T., 2012, Introduction to Infrared Spectroscopy, in Theophanides, T. (ed.), Infrared Spectroscopy - Materials Science, Engineering and Technology: InTech, 1-12, https://doi.org/10.5772/49106

Toby, B.H., Von-Dreele, R.B., 2013, GSAS-II: the genesis of a modern open-source all purpose crystallography software package: Journal of Applied Crystallography, 46, 544-549. https://doi.org/10.1107/S0021889813003531

Wang, Q., Li, W., Liu, R., Zhang, K., Zhang, H., Fan, S., Wang, Z., 2019, Human and non-human bone identification using FTIR spectroscopy: International Journal of Legal Medicine, 133, 269-276. https://doi.org/10.1007/s00414-018-1822-8

Weiner, S., Bar-Yosef, O., 1990, States of Preservation of Bones from Prehistoric Sites in the Near East: A Survey: Journal of Archeological Science, 17(2), 187-196. https://doi.org/10.1016/0305-4403(90)90058-D

Weiner, S., Brumfeld, V., Marder, O., Barzilai, O., 2015, Heating of flint debitage from Upper Paleolithic contexts at Manot Cave, Israel: Changes in atomic organization due to heating using infrared spectroscopy: Journal of Archeological Science, 54, 45-53. https://doi.org/10.1016/j.jas.2014.11.023

Xu, B., Poduska, K.M., 2014, Linking crystal structure with temperature sensitive vibrational modes in calcium carbonate minerals: Physical Chemistry Chemical Physics, 16, 17634-17639. https://doi.org/10.1039/c4cp01772b

Yu, S., You, X., Mou, Y., Jiang, X., Ou, W., Zhou, L., 2013, A New Approach for Spectra Baseline Correction Using Sparse Representation: Proceedings of the IASTED International Conference, Phuket Thailand. https://doi.org./10.2316/P.2013.798-076

Zhang, F., Tang, X., Tong, A., Wang, B., Jingwei, W., Lv, Y., Tang, C. Wang, J., 2020, Baseline correction for infrared spectra using adaptive smoothness parameter penalized least squares method: Spectroscopy Letters, 53(3), 222-233. https://doi.org/10.1080/00387010.2020.1730908

Zhang, F., Tang, X., Li, L., 2022, Origins of Baseline Drift and Distortion in Fourier Transform Spectra: Molecules, 27(13), 4287. https://doi.org/10.3390/molecules27134287

Peer Reviewing under the responsibility of Universidad Nacional Autónoma de México.

This is an open access article under the CC BY-NC-SA license(https://creativecommons.org/licenses/by-nc-sa/4.0/)