Boletín de la Sociedad Geológica Mexicana Volumen 76, núm. 2, A101223, 2024 http://dx.doi.org/10.18268/BSGM2024v76n2a101223

Desarrollo de un método de clasificación de pastas cerámicas basado en el análisis de imágenes de radiografía digital

Development of a classification of ceramic paste based on the analysis of digital radiography images

Alan Nagaya¹, Rodrigo Tlacuilo¹, Oscar G. de Lucio^1,*, Soledad Ortiz²

¹ Laboratorio Nacional de Ciencias para la Investigación y Conservación del Patrimonio Cultural, Universidad Nacional Autónoma de México, Ciudad Universitaria, 04510 Coyoacán, CDMX, Mexico.

² Instituto de Investigaciones Antropológicas, Universidad Nacional Autónoma de México, Ciudad Universitaria, 04510 Coyoacán, CDMX, Mexico.

* Autor para correspondencia: (O. G. de Lucio) This email address is being protected from spambots. You need JavaScript enabled to view it.

Cómo citar este artículo:

Nagaya, A., Tlacuilo, L., de Lucio, O.G., Ortiz, S., 2024, Desarrollo de un método de clasificación de pastas cerámicas basado en el análisis de imágenes de radiografía digital: Boletín de la Sociedad Geológica Mexicana, 76 (2), A101223. http://dx.doi.org/10.18268/BSGM2024v76n2a101223

Manuscrito recibido: 12 de septiembre de 2023; manuscrito corregido: 1 de octubre de 2023; manuscrito aceptado: 1 de enero de 2024.

RESUMEN

El uso de los rayos X ha impulsado la aplicación de técnicas de imagen en el área de las Ciencias del Patrimonio, proveyendo una herramienta que aporta información global del objeto de estudio. El análisis de las radiografías digitales ofrece información con significado físico que relaciona las propiedades materiales del objeto con la atenuación de los fotones, y que puede ser extraída mediante el procesamiento digital de las imágenes. En este trabajo se presenta la caracterización de un sistema de radiografía digital, y se propone un método de análisis de tiestos cerámicos, basado en el estudio de los histogramas, que describen a las distribuciones de intensidad de los píxeles que conforman cada imagen. El objetivo de esta propuesta es entonces proveer una herramienta basada en un análisis matemático, que comprende un ajuste Lorentziano a las distribuciones del histograma de cada imagen y una clasificación por análisis de grupos, que permita establecer diferencias entre pastas cerámicas. Al aplicar este método logramos distinguir seis grupos de pastas, a partir de un conjunto formado por 275 objetos cerámicos (arqueológicos y contemporáneos) provenientes del Área Maya.

Palabras clave: cerámica, radiografía digital, rayos X, análisis de imágenes, ciencias del Patrimonio.

ABSTRACT

X-rays have motivated the application of imaging techniques in Heritage Sciences, providing a tool that produces global information about the object. The radiography analysis generates information with physical meaning relating the material properties with the photon attenuation. In this work, the characterization of a digital radiography system is presented, and the basis of an analysis method for ceramics sherds is described, based on the study of histograms, which represent the distribution of pixel intensities that made the image. Thus, this study aims to provide a tool, based on a mathematical analysis, encompassing a Lorentzian fit to each image histogram and a cluster analysis, that leads to establish a contrast between ceramic pastes. By applying this method, we could distinguish six paste groups from a set of 275 ceramic objects (archaeological and contemporary) from the Maya region.

Keywords: ceramics, digital radiography, X-rays, image analysis, Heritage sciences.

1. Introducción

El descubrimiento de los rayos X en 1895 produjo un gran interés científico relacionado con describir sus propiedades y encontrar aplicaciones para éstos. En 1896 se publicaron 49 monografías y 1044 artículos relacionados con este tema, cubriendo una gran variedad de campos científicos, entre ellos la radiología (Banerjee, 2012). Para 1897, el Dr. Charles Lester Leonard, realizó las primeras radiografías de objetos pertenecientes al patrimonio cultural. El Dr. Leonard radiografió la momia Mochica, proveniente de excavaciones peruanas, en la Universidad de Pennsylvania (Fiori y Nunci, 1995). Una de las primeras aplicaciones de la radiografía a cerámicas arqueológicas fue la realizada por Titterington (1935), donde presenta la radiografía de siete objetos hallados en un entierro de un pueblo nativo norteamericano con el fin de mostrar la morfología de las inclusiones.

Las radiografías se producen debido a la interacción de los rayos X con la materia. A nivel microscópico, los rayos X interaccionan con los átomos que conforman la materia y su energía se puede absorber, dispersar o transmitir (Iowa State University, Center for Nondestructive Evaluation), provocando una diferencia de contraste. La ecuación que describe esta interacción es la ley de Beer–Lambert (Ecuación 1), donde la razón de la intensidad final (l) respecto de la intensidad inicial (l₀), decrece exponencialmente y depende del coeficiente de atenuación lineal del material (m₁) y la distancia que recorra el fotón dentro de este (c) (Agarwal, 1991).

(1)

Bajo las condiciones adecuadas las radiografías han sido utilizadas para determinar los procesos primarios de manufactura y caracterizar pastas cerámicas determinando el tamaño, proporción, tipo y mineralogía general de las inclusiones, así como materiales desgrasantes (Berg, 2008).

Trabajos pioneros como los realizados por Rye (1977), donde se describen características de cerámicas según su manufactura; Blakely et al. (1989), propone un método de análisis basado en las inclusiones de las cerámicas, logrando agruparlas según sus características físicas y su origen geográfico; fueron realizados usando técnicas análogas, xerorradiografía (Carr, 1990), una técnica que registra las imágenes de rayos X en una placa de aluminio recubierta de selenio (Rodríguez Salvador, 2012).

Los avances tecnológicos del siglo XX promovieron el uso de técnicas más eficientes y que produjeran menos desechos químicos. Así, en 1980 es introducida la radiografía computarizada (CR, por sus siglas en inglés). Que sustituyó la placa radiológica por un casete, que posteriormente era revelado con un lector láser (Gálvez, 2013). Sin embargo, los altos requerimientos técnicos y los costos de financiamiento retrasaron su uso (Körner et al., 2007).

En la década de 1990, gracias al desarrollo de la tecnología Flat Panel (panel plano), se introdujo la radiografía digital directa (DR, por sus siglas en inglés). En esta se elimina la necesidad de un sistema de revelado, contando con un convertidor que transforma los rayos X a luz (Gálvez, 2013; Casali, 2006).

Existen dos tipos de detector de panel plano, que se clasifican según su sistema de detección. La detección directa incorpora un fotoconductor que produce una corriente eléctrica, el material más común para el fotoconductor es selenio amorfo (a-Se) de entre 0.5 mm a 1 mm de grosor. El elemento que lee la carga eléctrica está compuesto por un electrodo que colecta la carga eléctrica generada y un capacitor que la almacena. Por otra parte, en la detección indirecta el panel incorpora un material centelleante, comúnmente yoduro de cesio (Csl), que produce un fotón de luz visible al absorber el fotón de rayos X. Este fotón de luz visible es el que produce la corriente eléctrica en un fotodiodo, típicamente de silicio amorfo (a-Si) (Ristic, 2013). Cuando la corriente eléctrica es producida, esta se lee por un arreglo generalmente de a-Si,el cual tiene asociado transistores de películas delgadas (llamados TFT por sus siglas en inglés), generando así una señal que pasa por un multiplexor. La generación de la radiografía digital concluye con el procesamiento de la señal por un software digitalizador que discretiza los niveles de gris, produciendo así una imagen digital (Casali, 2006; Ristic 2013).

Una imagen digital es una matriz de dos dimensiones (n×m), donde cada celda es conocida como píxel (del inglés PICture ELement), y se encuentra caracterizado por un vector de posición (n_i, m_j), y contiene información escalar (niveles de grises) o vectorial (imágenes en color) (van der Stelt, 2008). Una radiografía digital vive entonces en la convergencia de dos espacios discretos, el primero corresponde al muestreo espacial, y el segundo a la señal registrada por el detector, traducida como una escala de grises, el cual depende de las características materiales del objeto estudiado, y queda descrito por la Ecuación (1) (Casali, 2006).

Trabajar con radiografías digitales ofrece ventajas como la reducción a la exposición a la radiación, el almacenamiento digital de las imágenes, la transmisión de ellas sin pérdida de información y la posibilidad de manipularlas directamente (Forsyth et al., 1996).

La manipulación de imágenes digitales se divide entre procesamiento digital de imágenes (DIP, por sus siglas en inglés) y análisis de imágenes. Cuando se ajustan los parámetros de la imagen para resaltar información se utiliza el término procesamiento de imágenes (van der Stelt, 2008), el cual está basado en emplear técnicas basadas en diversos filtros matemáticos bien establecida desde hace décadas (Gonzalez y Wintz, 1987) que transforman y mejoran la imagen, ya sea discriminando o resaltando las características de interés (Kaur y Kaur, 2015). Cuando el usuario realiza cálculos por medio de software dedicado para extraer información específica de la imagen se considera que se realiza el análisis de imagen (van der Stelt, 2008) por ejemplo, a través de la descripción del histograma o del perfil de niveles de gris (Coady et al., 2019).

Existe una gran variedad de códigos desarrollados específicamente para el análisis de imágenes en escala de grises (como es el caso de radiografía digital). Entre los que se encuentra la segmentación (también conocida como umbralización o método del valor umbral), que permite seleccionar píxeles con nivel de gris I_U(n_i,m_j) , eligiendo un valor umbral T tal que

(2)

donde t₀ y t₁ son los dos posibles niveles de gris, cuando t₀ = 0 y t₁ = 1, recibe el nombre de binarización, I(n_i,m_j) es el nivel de gris del píxel en la posición (n_i,m_j) (Triana et al., 2016). Existen distintos métodos para determinar T, los propuestos por Zack et al., (1977), Otsu (1979), Kapur et al., (1985), Yen et al., (1995), son algunos ejemplos. Este filtro nos permite resaltar información, dependiendo de cómo se elija el valor T, ya sea de manera local o global en una imagen.

La inversión, es un proceso por el cual se transforma el valor de nivel de gris de la imagen siguiendo la ecuación,

(3)

donde n, es la profundidad de niveles de gris en bits (Davarinejad, 2015). En el caso de radiografía digital, si la información está en formato negativo, con este proceso empatamos la información de la imagen con la descripción física de la ley de Beer-Lambert (Ecuación 1), donde 2ⁿ significa que la radiación no se atenuó (blanco) y 0 significa que la radiación se atenuó completamente (negro). La imagen procesada con este filtro se conoce como imagen en positivo. En este trabajo todas las radiografías son tratadas con este filtro a manera de pre-procesamiento.

Otros filtros que han sido usados son, Histéresis diferencial, que resalta detalles en conjuntos pequeños de píxeles a partir de una interpolación de píxeles vecinos (Blotta y Moler, 2004); Falso color, que ayuda a detectar a simple vista los detalles debido a que el ojo humano es más sensible a una gama de colores que a una escala de gris (Dmitruk et al., 2017); Máscara de Enfoque, que mejora la definición de las imágenes, resaltando contrastes entre estructuras, y que ha permitido la descripción de las diferentes técnicas de manufactura cerámica en un amplio número de investigaciones (Berg y Ambers, 2016).

Avances recientes en el análisis de radiografías digitales de cerámicas pueden encontrarse condensados en el software ShiVA, desarrollado por Greene et al. (2017), donde las radiografías son sometidas a una serie de transformaciones, manipulaciones y cuantificaciones que permiten analizar los histogramas en busca de densidad, forma, y otras características de huecos, inclusiones y gradientes de matriz. Otros avances buscan métodos de captura 3D, que proveen la información completa del objeto (Adamovic y Zivic, 2021).

El propósito de este trabajo es desarrollar una metodología no invasiva y no destructiva aplicable a cerámicas (arqueológicas o contemporáneas), con el fin de determinar características físicas de la pasta, y que permita establecer de manera sistemática e independiente del observador una clasificación de éstas. Dicha metodología está basada en el análisis de histogramas de las radiografías digitales, ajustándoles una distribución Lorentziana, en donde, los parámetros del ajuste se encuentran relacionados con las propiedades físicas de la pasta.

También fue necesaria la caracterización y optimización del sistema y procedimiento de adquisición de radiografías digitales con el fin de distinguir artefactos o errores sistemáticos que pudieran estar presentes en las imágenes analizadas.

2. Materiales y métodos

2.1. Materiales

Se analizaron un total de 275 tiestos de objetos cerámicos, divididos en tres grupos provenientes de contextos arqueológicos distintos procedentes de la misma región geográfica, el Norte de la Península de Yucatán. La Figura 1 muestra las fotografías de los tiestos representativos, seleccionados de tal forma que presenten todas las características que se describirán a continuación.

Figura 1. Se muestran algunos de los objetos cerámicos estudiados, representativos de los grupos de pastas encontrados.

2.2. Análisis de Imágenes

Para realizar el análisis de las radiografías se utilizó el software de uso libre ImageJ, desarrollado originalmente para microscopía digital médica por Wayne Basband, (Collins, 2007) que ha demostrado ser muy útil en aplicaciones para el estudio de radiografías digitales, como se muestra en los trabajos realizados por Geiger, et. al. (2016) y Satir, et. al. (2021), debido a que cuenta con herramientas de análisis como histogramas, perfiles de grises, conteo de partículas, estadística multivariable, calibraciones espaciales y de niveles de gris, pseudo-gráficas de superficie, análisis de regiones de integres, entre otras (National Institutes of Health, 2018).

Adicionalmente cuenta con una extensa biblioteca de filtros en forma de complementos (plugins) con diversas aplicaciones y alcances, que vienen preinstalados en el software como es el caso de la segmentación (con algoritmos del valor umbral implementados), operaciones (lógicas y aritméticas) entre imágenes, Contraste Local Mejorado (CLAHE, por sus siglas en inglés) (Zuiderveld, 1994), Mexican Hat Filter (Marr y Hildreth, 1980), Rolling ball background substractor (Sternberg, 1983), Mosaic Background Substractor (Sbalzarini y Koumoutsakos, 2005), Sigma Filtering (Lee, 1983), Ridge detection (Steger, 1998).

2.3. Descripción de una radiografía

Como se ha mencionado antes, una radiografía nos permite identificar diferentes características materiales en los objetos estudiados, a partir de una diferencia de contraste que se encuentra regida por la ecuación de Beer-Lambert (Ecuación 1) de la siguiente manera: Si la radiografía se encuentra en positivo, podemos distinguir las siguientes características (Figura 2): (i) La matriz presentará por lo general un nivel de gris uniforme; (ii) diferencias materiales: las vacancias se verán como regiones muy claras y acotadas, mientras que las inclusiones se distinguen como regiones oscuras muy localizadas, el nivel de gris depende fuertemente de la composición química de éstos; (iii) cambios en el espesor: un adelgazamiento se representará como una región clara y extendida, mientras que una zona de mayor espesor se verá como una región más oscura (ambos respecto de la matriz de la pasta); (iv) efecto volumétrico: las curvaturas de los objetos se aprecian como zonas más oscuras, debido a que la sección transversal efectiva es mayor en esas regiones; (v) las grietas se verán en el mismo nivel de gris que las zonas correspondientes al fondo. Las características (iv) y (v) son siempre evidentes en una observación simple del objeto.

Figura 2. Descripción de los elementos analizados en una radiografía.

2.4. Equipo de Radiografía Digital

El equipo de radiografía digital con el que se cuenta en el LANCIC-IF UNAM, está compuesto de cuatro partes. La fuente de rayos X, un sistema portátil POSKOM PXM-40BT (Figura 3a), que irradia rayos X en un intervalo de voltaje de tubo 40-100 kV (±7%) en pasos de1 kV; con un intervalo de corriente de tubo 0.4-100 mA∙s (±10%) en 35 pasos no uniformes. Además de las siguientes características reportadas por el fabricante, un punto focal del tubo de 1.2×1.2 mm; ángulo de blanco de tungsteno de 16°; filtraje intrínseco de 0.8 mm equivalente de Al @ 100 kV; capacidad calórica del ánodo de 14 kJ.

Figura 3. a) Fuente de rayos X portátil POSKOM PXM-40BT. b) Detector de rayos X de panel plano Vidisco Imager FlashX Pro. c) Unidad de control de interfaz Vidisco ICU.

La segunda parte es el detector de rayos X Vidisco Imager FlashX Pro (Figura 3b), un detector de panel plano de conversión indirecta compuesto por un fotodiodo de silicio amorfo (a - Si) con oxisulfuro de gadolinio (GdOS) como material fluorescente. De acuerdo con el fabricante, cuenta con un área de imagen efectiva de 43.2×34.2 cm, y una profundidad máxima de niveles de gris de 16 bits (2₁₆=65,535 niveles de gris), una resolución ~3.5 lp∙mm^-1, que equivale a un tamaño de píxel de 144 mm o 180 dpi.

El sistema de radiografía se completa con la unidad de control Vidisco ICU (Figura 3c), que funciona como la interfaz en tiempo real entre el detector y la computadora de control. La unidad de control se conecta de forma alámbrica al detector y con la computadora, aunque existe la posibilidad de conectarse de forma inalámbrica. Por último, el último elemento del sistema es la computadora de control que cuenta con el software Vidisco Xbit, que procesa la imagen digital y la puede exportar en distintos formatos, como JPG o TIFF.

Los parámetros más importantes para caracterizar una radiografía quedan dados entonces por el voltaje “kV”, y la corriente “mA∙s” de tubo, y la distancia irradiador – objeto (DIO), o la distancia irradiador – detector (DID), cuando es posible medirla.

2.5. Caracterización y optimización del equipo

Se midió el haz efectivo de radiación a una distancia de 1 y 2 m colocando el detector en diferentes posiciones y después uniendo las imágenes en un mosaico. La Figura 4a muestra la radiografía en positivo del mosaico del cono de radiación (sin colimador) del irradiador para una distancia irradiador-detector (DID) de 1.00±0.02 m.

Como se observa en la Figura 4a, hacia los extremos la radiación se atenúa significativamente y forma bordes suaves. Con el fin de determinar los límites donde la radiación fuera máxima y uniforme, se midieron los perfiles de niveles de gris en diferentes posiciones (vertical y horizontal), Obteniendo que el área efectiva de irradiación a 1 m es de 28.9×31 cm, comparándola con la reportada por el fabricante, es menor un 59.44% (Figura 4b).

Figura 4. a) Cono de radiación producida por la fuente de rayos X portátil POSKOM PXM-40BT. Radiografía en positivo con parámetros de irradiación: 45 kV, 40 mA∙s, DID: 1.00±0.05 m. La imagen está compuesta por un mosaico de 6 radiografías, para su ensamble se utilizó como referencia el riel y las abrazaderas que aparecen en la imagen. Tomada por O. G. de Lucio y R. Tlacuilo. b). Comparación de las áreas de análisis. En amarillo se muestra el área dada por la luz guía del colimador, en gris el área efectiva reportada por el fabricante y en negro el área calculada.

En la Figura 5 se muestra la radiografía del cono de radiación del irradiador para una DID: 2.0 ± 0.02 m. Como la distancia es el doble, hay mayor dispersión y atenuación de los rayos X en el aire. En este caso se observa que el área de radiación uniforme es de 58.1×38.6.

Figura 5. Cono de radiación producido por la fuente de rayos X portátil POSKOM PXM-40BT. Radiografía en positivo con parámetros de irradiación: 45 kV y 40 mA∙s, DID: 2.00±0.05 m. La imagen está compuesta por un mosaico de 22 radiografías, para su ensamble se utilizó como referencia el riel y las abrazaderas que aparecen en la imagen.

Con el propósito de verificar la resolución dada por el fabricante, se midió previamente la resolución espacial efectiva, obteniendo que el tamaño de píxel era de 135±10 mm (Tlacuilo González, 2018). Con el fin de verificar la medición, siguiendo la metodología propuesta en este trabajo, se obtuvo el perfil de grises de un alfiler de 0.7±0.5 mm de diámetro, DIO: 1.00±0.05 m, (Figura 6a). En el ajuste gaussiano del perfil para el alfiler, se obtuvo que el FWHM es de 5.16±0.03 px, (Figura 6b), por lo que la dimensión de un solo píxel es de136 ± 2 mm. Lo cual representa un error de 6% respecto a lo reportado por el fabricante.

Figura 6.  a) Radiografía en positivo de un alfiler bajo condiciones de irradiación de 40 kV y 36 mA∙s, DIO:1.00±0.05 m. b) Ajuste gaussiano del perfil de grises del alfiler.

Usando la ecuación de estimación de tamaño de píxel (Ecuación 4) (Scientific Imaging, Inc., 2021), obtenemos entonces que la resolución del detector es de 3.67±0.05 lp∙mm^-1. Siendo un mayor que lo reportado.

(4)

De igual forma es posible calcular cuántos píxeles hay en una pulgada, dividimos la longitud de la pulgada entre el tamaño de píxel, obteniendo una resolución de 187±3 dpi, siendo un 4% mayor respecto a lo reportado. Con este valor podemos determinar el área efectiva del detector, debido a que las dimensiones de la imagen son de 2994 ×2397 px, equivalen a (40.7±0.03)×(32.5±0.02) cm. Siendo menor un 7% y 5% respectivamente en cada dimensión, respecto a lo informado por el fabricante.

Por último, se midió el límite donde podemos considerar haces paralelos en el cono de radiación, para lo cual se radiografió un disco de grafito de 17.40±0.05 mm de diámetro y 12.00±0.05 mm de grosor, a distancias variables (Figura 7), obteniendo que en las distancias de trabajo (hasta 2 m), los haces de rayos X se comportan como rayos paralelos.

Figura 7. Radiografía en positivo de un disco de grafito. La radiografía se tomó bajo condiciones de irradiación: 40 kV. a) 2 mA∙s, DID: 0.50±0.05 m. b) 6.4 mA∙s, DID:1.00±0.05 m. c) 15 mA∙s, DID: 1.50±0.05 m. a) 21 mA∙s,DID: 2.00±0.05 m. Tomadas por O. G. de Lucio y R. Tlacuilo.

2.6. Análisis de histogramas

Con el fin de establecer un método de comparación entre pastas se requiere que las condiciones de irradiación sean equivalentes, para así determinar los parámetros operacionales. Se radiografió una cerámica contemporánea desde 40 kV hasta 100 kV en intervalos de 10 kV, modificando las corrientes de tubo, con el propósito de que no hubiera pérdidas de información en el objeto (“píxeles quemados”). Se midió el perfil de grises sobre la línea indicada en la Figura 8a-c. Como referencia se utilizó una escala de aluminio, con la cual se parametrizan los niveles de gris de los perfiles entre las diferentes imágenes, eliminando así la dependencia con la corriente.

Figura 8. Radiografías tomadas bajo condiciones de radiación DID: 1.00±0.05 m a) 40 kV y 50 mA∙s, b) 60 kV y 9 mA∙s, c) 100 kV y 2 mA∙s. d) Contraste para las siete energías utilizadas. e) y su derivada.

A partir de la ecuación de contraste (Ecuación 5, donde I_b es el nivel de gris del fondo y I_i es el nivel de gris del píxel al que se le busca el contraste (Pacella, 2015), se obtuvo el contraste del perfil (Figura 8d), y posteriormente el contraste diferencial (Figura 8e). Con lo anterior se observó que las variaciones más significativas en el contraste se dan cuando las radiografías se adquieren empleando energías bajas (40-50 kV), se observa también que hay anomalías en el contraste para energías arriba de 70 kV. Como resultado de este análisis, y para maximizar el contraste, los parámetros de operación se establecieron en 45 kV y 40 mA·s y a una distancia fuente-detector fija de 2 m, con los objetos de estudio colocados en contacto con el detector. Las radiografías resultantes tienen una profundidad de 8 bits (Figura 9), con el fin de no generar archivos excesivamente grandes, pero que resulta suficiente para poder realizar análisis adecuados (Casali, 2006).

(5)

El análisis de histogramas de las imágenes radiográficas es una herramienta poderosa, por lo que nos basamos en la descripción de éstos para proponer un método de clasificación de pastas cerámicas. Este análisis consiste en distinguir diferencias en las densidades radiológicas presentes en el objeto de estudio, a partir de los cambios en el contraste lo cual puede verse como distribuciones aisladas o una superposición de estas en el histograma. La conexión entre la información contenida en el histograma y las características materiales queda dada una vez más por la Ecuación 1.

Figura 9. Se muestran las radiografías de algunos de los objetos cerámicos estudiados, representativos de los grupos de pastas encontrados.

El caso más sencillo para ilustrar el comportamiento de las densidades radiológicas se muestra en la Figura 10a. El cual corresponde a la radiografía de cuatro láminas de aluminio de distintos espesores, de esta manera se modifica únicamente la variable x en la Ecuación 1. Esto nos permite generar una imagen radiográfica con cuatro densidades radiológicas, caracterizadas por cuatro niveles de grises. El histograma normalizado como función de densidad (normalizado entre el número total de píxeles, haciendo que la integral bajo la curva sea 1), de esta imagen se muestra en la Figura 10b. En dicho histograma se observan cuatro bandas, con este ejemplo es fácil ver la correspondencia entre las bandas del histograma y la imagen. La región de aluminio más delgada (segmento derecho de la imagen) corresponde a la banda con máximo en 209, mientras que la región de aluminio más gruesa (segmento izquierdo de la imagen) corresponde a la banda con máximo en 115.

Figura 10. a) Radiografía en positivo de la escala de láminas de aluminio con grosores de 6.50 mm, 4.60 mm, 3.90 mm y 2.90 mm (de izquierda a derecha); obtenida bajo condiciones de irradiación: 40 kV y 40 mA∙s, DID: 1.00±0.05 m, con profundidad de 8 bits. Tomada por O. G. de Lucio y A. Nagaya. b) Histograma de la zona correspondiente a las láminas de aluminio. c) Segmentación en el intervalo 207-211, usando la Ecuación (7).

Para mostrar la equivalencia entre el nivel de gris y el espesor de la escala correspondiente, se realiza una segmentación con la siguiente metodología. Cada banda en el histograma puede ser ajustada mediante una distribución Lorentziana (Ecuación 6). Tomando como ejemplo la zona de menor densidad radiológica, el ajuste tiene parámetros A=0.27, y₀= -9.10×10^-4, ω=2.37 y xc=208.99.

(6)

A partir de los cuales definimos la función segmentación en la Ecuación 7, obteniendo que la imagen resultante del proceso es la Figura 11c.

(7)

Este proceso únicamente resaltó la zona de menor densidad radiológica. Se observa que hay píxeles no segmentados dentro de la región resaltada. Analizando la imagen con una segunda segmentación, solo seleccionamos la región más delgada de la Figura 10a y ahora segmentamos según la Ecuación 8, el resultado se muestra en la Figura 11. De color azul se resaltan zonas con menores densidades radiológicas, mientras que, de color verde se resaltan zonas con mayores densidades radiológicas en el mismo objeto. Las zonas no segmentadas pueden ser resultado de imperfecciones en el objeto, por un mal pulimiento o golpes microscópicos en las láminas, que alteran el espesor.

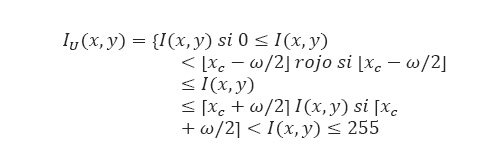(8)

Podemos ver entonces que el comportamiento de distintas densidades radiológicas en el material producirá distintas bandas en el histograma de la radiografía digital, que pueden ser descritas mediante distribuciones Lorentzianas. Además, la segmentación puede asociarse con características materiales del objeto.

Figura 11. Segmentación en el intervalo 0-206 (azul); y segmentación en 212-255 (verde), de la región más delgada en la escala de láminas de aluminio.

En el caso de los objetos cerámicos, los parámetros ajustados se relacionan con las propiedades cerámicas. El intervalo segmentado por la Ecuación 7, corresponde a la matriz de la pasta. Las zonas de mayor densidad radiológica corresponden a inclusiones o materiales desgrasantes en la pasta. Mientras que las zonas de menor densidad radiológica corresponden a las vacancias presentes en la pasta, relacionados principalmente con su cocido (Rice, 1987). La Figura 12, muestra las características presentes en un objeto cerámico, resaltadas por segmentación.

Figura 12. a) Segmentación de la matriz cerámica en un objeto del clásico temprano. b) Segmentación de las inclusiones y (posibles) desgrasantes en azul y de las vacancias o regiones con adelgazamiento en verde.

Otro resultado importante de este ajuste Lorentziano es que el parámetro ω caracteriza al material independientemente de su espesor, si aplicamos la Ecuación 7, sustituyendo el nivel de gris central (x_c), para cada banda, obtenemos la segmentación presentada en la Figura 13, al ajustar esas bandas observamos que los valores de ω son muy similares. Un objeto hecho del mismo material que otro tendrá valores ω similares sin importar su espesor. En el caso cerámico, la matriz determinada por el parámetro ω siempre presentará el mismo ancho en los intervalos de gris.

Figura 13. a) Segmentación en el intervalo 169-173. b) Segmentación en el intervalo 136-140. a) Segmentación en el intervalo 113-117. De la escala de aluminio.

3. Resultados

Tras obtener el histograma para cada imagen radiográfica y ajustar la distribución Lorentziana a éste, se agruparon las pastas según los parámetros de ajuste x_c y ω calculados (Ecuación 6), buscando que fueran similares (±2%), en un total de 34 grupos. Después de hacer un análisis de grupos (cluster analysis) siguiendo la metodología de (Karasik y Smilansky, 2011) aplicada a los parámetros del ajuste se obtiene que los objetos se agrupan en seis tipos de pasta diferente (Figura 14). En la Tabla 1, se describen las características representativas de estos grupos.

Figura 14. Dendrograma de la preclasificación de grupos, se utilizó una distancia del tipo Euclidiana, encontrando el centro por suma de distancias.

Tabla 1. Grupos de pastas encontrados, radiografías de objetos característicos de cada grupo y descripción de sus características principales.

Tabla 1. Continuación

4. Discusión

Los objetos no siempre son lisos, en algunas ocasiones presentan esgrafiados, decoraciones o incluso cambios en su espesor debidos al uso, ver Figura 15a, también pueden ser curvos o de espesores variables, y de acuerdo con la Ecuación 1 esto modifica el contraste, lo cual no se puede discriminar de manera directa al momento de adquirir las imágenes radiográficas (ver Figura 15b). Para reducir estos efectos es necesario tomar solo una sección representativa del material, para lo cual definimos regiones de por lo menos 1 cm² de área, donde la pasta se comporta de manera “uniforme”. Esto evita que un mismo histograma pueda presentar distribuciones adicionales de niveles de gris, que no estén asociadas únicamente a las propiedades materiales de las pastas, sino más bien a factores geométricos, como los detalles de diseño y la forma del objeto.

Figura 15. a) Histograma del objeto perteneciente al grupo clásico tardío del contexto arqueológico 1. b) Histograma del objeto perteneciente al grupo sin identificar del contexto arqueológico 2.

El valor ω, relacionado con las propiedades de la matriz de la pasta, es además un indicador de la homogeneidad de ésta, y puede utilizarse para dar una descripción a primera aproximación, de manera no–invasiva y no–destructiva. Para valores de ω pequeños se tiene que la pasta es significativamente homogénea, las inclusiones y las vacancias no son identificadas en la radiografía de manera evidente, ya sea por su tamaño pequeño, o porque no hay una presencia notable de éstas.

La pasta 1 y la pasta 4, son las que mayor cantidad de objetos agrupa, estas se caracterizan por tener un valor ω intermedio. Los objetos de la pasta 1 tienden a presentar un mayor número de vacancias, por lo que su distribución en el histograma presenta un corrimiento hacia el blanco y la aparición de un hombro alrededor del nivel de gris 180 (Figura 16), las vacancias no tienen una morfología uniforme y sus tamaños no son constantes, aunque su presencia y número podrían indicar detalles en la manufactura relacionados con el proceso de cocido. Aunque también podría estar relacionado con un desgaste debido al uso que tuvo durante su vida útil. Por otra parte, los objetos de la pasta 4 tienden a presentar un mayor número de inclusiones (que típicamente tienen más densidad radiológica), por lo que su distribución en el histograma tiene un corrimiento hacia el negro (Figura 16), la morfología de estas inclusiones es circular o tabular, distribuida uniformemente en toda la matriz. Por la forma de estas inclusiones pueden ser inclusiones de carbonato de calcio o inclusiones de granito (Berg, 2008).

Figura 16. Histogramas de los objetos representativos de las pastas 1 (verde) y 4 (rojo).

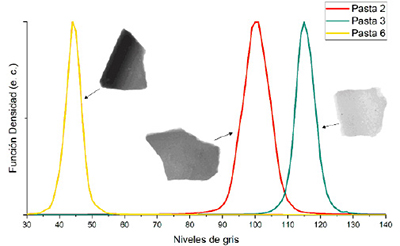
Las pastas 2, 3, 6 que se caracterizan por presentar valores ω pequeños tienen distribuciones simétricas (Figura 17), la principal diferencia entre estos grupos es la ubicación del máximo del nivel de gris. La Pasta 3, es la de menor densidad radiológica, mientras que la Pasta 6 se caracteriza por tener la mayor densidad radiológica.

Figura 17. Histogramas de los objetos representativos de las pastas 2 (rojo), 3 (verde) y 6 (amarillo).

La Pasta 5 es la que presenta la menor homogeneidad, relacionada con un alto contenido de vacancias e inclusiones, su distribución es asimétrica, presenta hombros alrededor de los niveles de gris 90 y 140 (Figura 18). Las inclusiones presentes comparten características con las de la pasta 4, y al igual que con la pasta 1, las vacancias no presentan una tendencia evidente. Lo cual no está ligado únicamente al proceso de manufactura del objeto, sino que podría estar relacionado también con su uso y función.

Figura 18. Histograma de los objetos representativos de la pasta 5.

5. Conclusiones

El método de clasificación presentado en este trabajo permite establecer relaciones entre los objetos cerámicos, considerando las características de la matriz del objeto, las inclusiones y vacancias de esta mediante un método no invasivo y no destructivo, y hasta cierto grado independiente del observador. De acuerdo con nuestros resultados, el método funciona de manera óptima cuando se trabaja con tiestos planos donde los detalles geométricos sean mínimos debido a que aquí el ajuste Lorentziano representa mejor las características materiales de la pasta. Observamos algunas dificultades al aplicar el método cuando el tiesto presenta curvatura porque los histogramas muestran alteraciones en sus extremos. Finalmente, en el caso de objetos completos, se debe de seleccionar una región que sea lo más paralela al frente de onda para evitar los cambios de grosor aparente que se presentan hacia las orillas (sección transversal).

Consideramos que este método complementa técnicas destructivas como la petrografía, ya que permite definir regiones de interés, a partir de identificar la posición de las inclusiones y vacíos. Esta metodología logra optimizar los cortes de las láminas delgadas de los objetos, y a su vez es complementado por técnicas espectroscópicas mediante las cuales podríamos identificar los materiales presentes en las pastas. Las características de la matriz y su homogeneidad, así como la presencia de inclusiones y materiales desgrasantes pueden ser indicadores del grado de similitud de materiales con la matriz, la manera en que fueron molidos o la incorporación de tiestos molidos. Para extraer esta información de las imágenes radiográficas es necesario considerar un análisis más detallado que incluya los efectos de volumen, y la atenuación de los diferentes materiales presentes. Las diferencias en la presencia de vacancias (ya sea número, orientación o forma) es un indicador de la técnica de manufactura que se empleó con el barro, de las condiciones en que las cerámicas fueron cocidas, y pueden dar información de la temperatura a la que fueron sometidas, ya que la cantidad de vacancias están relacionados a las temperaturas de horneado (Rice, 1987). Es necesario un algoritmo con un análisis matemático más sofisticado para definir el número de inclusiones y vacancias, sus características y morfología, el cual será desarrollado en un trabajo posterior, utilizando como base el método aquí propuesto.

A partir de un análisis basado en segmentación se pueden describir las inclusiones y materiales haciendo uso de los diversos algoritmos y procesos que el software ImageJ contiene. Ya existen protocolos y métodos para caracterizar las pastas, las inclusiones y los materiales desgrasantes, sin embargo, casi todos ellos son destructivos y depende en gran medida del observador y su experiencia. Los resultados de la clasificación de pastas obtenidos tienen un significado físico, dada la información contenida en las radiografías y el análisis matemático que se ha hecho. Sin embargo, no se han confrontado aún con las clasificaciones arqueológicas correspondientes, lo cual es de fundamental importancia para entender el significado de los objetos dentro de la sociedad que los creó.

Contribuciones de los autores

Conceptualización: de Lucio, O.G.; Análisis o adquisición de datos: de Lucio, O.G., Nagaya, A., Tlacuilo, R.; Desarrollo metodológico/técnico: de Lucio, O.G., Nagaya, A., Tlacuilo, R.; Redacción del manuscrito original: de Lucio, O.G., Nagaya, A.; Redacción del manuscrito corregido y editado: de Lucio, O.G., Nagaya, A., Ortiz, S.; Diseño gráfico: de Lucio, O.G., Nagaya, A., Tlacuilo, R.; Trabajo de campo: de Lucio, O.G., Nagaya, A., Tlacuilo, R., Ortiz, S.; Interpretación: de Lucio, O.G., Nagaya, A., Tlacuilo, R.; Financiamiento: de Lucio, O.G., Ortiz, S.; Dirección y Administración de proyecto: de Lucio, O.G., Ortiz, S.; Coordinación de proyectos arqueológicos y etnográficos: Ortiz, S.

Financiamiento

Este trabajo fue financiado por el proyecto CONAHCYT CF 2019 No. 731762; y los proyectos CONAHCYT LN293904, LN 299076, LN314846, LN315853. Así como por los proyectos DGAPA-PAPIIT IN101920, IN113321 e IN108521. Soledad Ortiz agradece el apoyo recibido durante su estancia posdoctoral, otorgado por CONAHCYT.

Agradecimientos

Los autores expresan su agradecimiento a las siguientes personas: A. Mitrani, por su apoyo técnico durante el trabajo de campo realizado y la asesoría impartida para la correcta operación de los equipos; J.G. Morales por su asesoría técnica y por su ayuda en la caracterización de materiales de referencia; M. Pérez por su asistencia durante el trabajo de campo y de laboratorio.

Los autores agradecen el apoyo del Laboratorio Nacional de Ciencias para la Investigación y Conservación del Patrimonio Cultural (LANCIC-IF), que permitió realizar todo el trabajo experimental, sin el cual no habría sido posible esta investigación.

Conflictos de interés

Los autores hacen constar que no existen conflictos de interés con otros autores, instituciones u otros terceros sobre el contenido (total o en parte) del artículo.

Editor a cargo

Avto Goguitchaichvili.

Referencias bibliográficas

Adamovic, D., Zivic, F., 2021, Hardness and Non-Destructive Testing (NDT) of Ceramic Matrix Composites (CMCs), Encyclopedia of Materials: Composites vol 2: Amsterdam, Elsevier, 183-201. https://doi.org/10.1016/B978-0-12-819724-0.00074-4

Agarwal, B.K., 1991, Interaction of X-Rays with Matter, in Agarwal, B. K., X-Ray Spectroscopy, an Introduction: Berlin, Springer, 105-153. https://doi.org/10.1007/978-3-540-38668-1_3

Banerjee, A.K., 2012, Los primeros días de la radiología, en Lee, S., Crean, M. (eds.), La historia de la radiología: Viena, Sociedad Europea de la Radiología (ESR), 25-34.

Berg, I., 2008, Looking through pots: recent advances in ceramics X-radiography: Journal of Archeological Science, 35(5), 1177-1888. https://doi.org/10.1016/j.jas.2007.08.006

Berg, I., Ambers, J., 2016, X-Radiography of Archeological Ceramics, in Hunt, A. (ed.), The Oxford Handbook of Archeological Ceramic Analysis: Oxford, Oxford University Press, 690 p.

Blakely, J.A., Brinkmann, R., Vitaliano, C.J., 1989, Pompeian Red Ware: Processing archeological ceramic data: Geoarchaeology: an International Journal, 4(3), 201-228. https://doi.org/10.1002/gea.3340040302

Blotta, E., Moler, E., 2004, Fingerprint image enhancement by differential hysteresis processing: Encyclopedia of Materials: Composites, 2, 183-201. https://doi.org/10.1016/B978-0-12-819724-0.00074-4

Carr, C., 1990, Advances in ceramics radiography and analysis: applications and potentials: Journal of Archeological Science, 17(1), 13-34. https://doi.org/10.1016/0305-4403(90)90013-U

Casali, F., 2006, Chapter 2 X-Ray and Neutron Digital Radiography and Computed Tomography for Cultural Heritage, in Bradley, D., Creagh, D. (eds.), Physical Techniques in the Study of Art Archeology and Cultural Heritage: London, Elsevier Science, 41-123.

Coady, J., O’Riordan, A., Gerard, D., Newe, T., Toal, D., 2019, An Overview of Popular Image Procesing Filtering Operations, in 2019 13th International Conference on Sensing Technology (ICST): Sydney, Australia, IEEE, 263-267. https://doi.org/10.1109/icst46873.2019.9047683

Collins, T.J., 2007, ImageJ for microscopy: BioTechniques, 43(suppl.1), 25-30. https://doi.org/10.2144/000112517

Davarinejad, H., 2015, Quantifications of western blots with Image J: University of York.

Dmitruk, K., Denkowski, M., Mazur, M., Mikolajczak, P., 2017, Sharpering filter for false color imaging of dual-energy X-ray scans: Signal, Image and Video Processing, 11, 613-620. https://doi.org/10.1007/s11760-016-1001-7

Fiori, M., Nunci, M.G., 1995, The earliest documented applications of X-rays to examination of mummified remains and archeological materials: Journal of the Royal Society of Medicine, 88(2), 67-69. PMCID: PMC1295097

Forsyth, D.B., Shaw, W.C., Richmond, S., 1996, Digital imaging of cephalometric radiography, part 1: advantages and limitations of digital imaging: Angle Orthod, 66(1), 37-42.

Gálvez, M.M., 2013, Algunos hitos históricos en el desarrollo del diagnóstico médico por imágenes: Revista Médica Clínica Las Condes, 24(1), 5-13. https://doi.org/10.1016/S0716-8640(13)70123-8

Geiger, M., Blem, G., Ludwig, A., 2016, Evaluation of ImageJ for Relative Bone Density Measurement and Clinical Application: Journal of Oral Health and Craniofacial Science, 1, 12-21. https://doi.org/10.29328/journal.johcs.1001002

Gonzalez, R.C., Wintz, P., 1987, Digital image processing: Estados Unidos, Addison-Wesley Longman Publishing, 503 p.

Greene, A.F., Hartley, C.W., Doumani, P.N., Chinander, M., 2017, The digital radiography of archeological pottery: Program and protocols for the analysis of production: Journal of Archeological Science, 78, 120-133. https://doi.org/10.1016/j.jas.2016.11.007

Iowa State University, Center for Nondestructive Evaluation, Interaction Between Penetrating Radiation and Matter, in X-Ray, Physics of Nondestructive Evaluation, disponible en <https://www.nde-ed.org/Physics/X-Ray/radmatinteraction.xhtml>, consultado 25 de marzo de 2022.

Kapur, J.N., Sahoo, P.K., Wong, A.K., 1985, A new method of gray-level picture thresholding using the entropy of the histogram: Computer Vision, Graphics and Image Processing, 29(3), 273-285. https://doi.org/10.1016/0734-189X(85)90125-2

Karasik, A., Smilansky, U., 2011, Computerized morphological classification of ceramics: Journal of Archaeological Science, 38(10), 2644-2657. https://doi.org/10.1016/j.jas.2011.05.023

Kaur, S., Kaur, P., 2015, Review and Analysis of Various Image Enhancement Techniques: International Journal of Computer Applications Technology and Research, 4(5), 414-418. https://doi.org/10.7753/ijcatr0405.1016

Körner, M., Weber, C.H., Wirth, S., Pfeifer, K. J., Reiser, M. F., Treitl, M., 2007, Advances in Digital Radiography: Physical Principles and System Overview.: RadioGraphics, 27(3), 675-686. https://doi.org/10.1148/rg.273065075

Lee, J.S., 1983, Digital image smoothing and the sigma filter: Computer Vision, Graphics, and Image Processing, 24(2), 255-269. https://doi.org/10.1016/0734-189x(83)90047-6

Marr, D., Hildreth, E., 1980, Theory of edge detection: Proceedings of the Royal Society of London B Biological Sciences, 702(1167) 187-217. https://doi.org/10.1098/rspb.1980.0020

National Institutes of Health, 2018, ImageJ Image Processing and Analysis in Java. Plugins (en línea): Maryland, Estados Unidos, disponible en <https://imagej.nih.gov/ij/plugins/index.html>, consultado el 03 de agosto de 2023.

Otsu, N., 1979, A Threshold Selection Method from Gray-Level Histograms: IEEE Transactions on Systems, Man and Cybernetics, 9(1), 62-66. https://doi.org/10.1109/tsmc.1979.4310076

Pacella, D., 2015, Energy-resolved X-ray detectors: the future of diagnostic imaging: Reports in Medical Imaging, 8, 1-13. https://doi.org/10.2147/rmi.s50045

Rice, P.M., 1987, Pottery Analysis A Sourcebook: Chicago, The University of Chicago Press, 559 p. https://doi.org/10.2307/281724

Ristic, G.S., 2013, The Digital Flat-Panel X-Ray Detectors, in Proceedings of the Third Conference on Medical Physics and Biomedical Engineering: Skopje, Association for Medical Physics and Biomedical Engineering, 65-71.

Rodríguez Salvador, J.J., 2012, Xerorradiografía: Imagen diagnóstica, 3(2), 67-69. https://doi.org/10.1016/j.imadi.2012.05.001

Rye, O. S., 1977, Pottery Manufacturing Techniques: X-Ray Studies: Archeometry, 19, 205-211. https://doi.org/10.1111/j.1475-4754.1977.tb00200.x

Satir, S., Buyukcavus, M. H., Kaan, O., 2021, A novel approach to radiographic detection of bucco-palatal/lingual dilacerations: a preliminary study with ImageJ: Proceedings of the Institution of Mechanical Engineers Part H: Journal of Engineering in Medicine, 235(11), 1310-1314. https://doi.org/10.1177/09544119211030717

Sbalzarini, I.F., Koumoutsakos, P., 2005, Feature Point Tracking and Trajectory Analysis for Video Imaging in Cell Biology: Journal of Structural Biology, 15(2), 182-195. https://doi.org/10.1016/j.jsb.2005.06.002

Scientific Imaging, Inc., 2021,. Optical Resolution of a Camera and Lens System (en línea), disponible en <https://scientificimaging.com/knowledge-base/optical-resolution-of-a-camera-and-lens-system/#:~:text=Camera%20pixel%20size%20limited%20resolution,3.45%20%3D%20145%20lp%2Fmm> consultado el 31 de agosto de 2022.

Steger, C., 1998, An unbiased detector of curvilinear structures: IEEE Transactions on Pattern Analysis and Machine Intelligence, 20(2), 113-125. https://doi.org/10.1109/34.659930

Sternberg, S., 1983, Biomedical Image Processing: Computer, 16(1), 22-34. https://doi.or

Titterington, P.F., 1935,. Certain Bluff Mounds of Western Jersey County, Illinois: American Antiquity, 1(1), 6-46. https://doi.org/10.2307/275856

Tlacuilo González, R., 2018, Caracterización de un sistema de radiografía digital con aplicaciones en el estudio del patrimonio cultural: Ciudad de México, Universidad Nacional Autónoma de México, Facultad de Ciencias, tesis de licenciatura, 118 p.

Triana, N., Jaramillo, A.E., Gutiérrez, R.M., Rodríguez, C.A., 2016, Técnicas de umbralización para el procesamiento digital de imágenes de GEM-Foils: Scientia et Technica, 21(4), 352-359. https://doi.org/10.22517/23447214.13271

van der Stelt, P.F., 2008, Better imaging, The advantages of digital radiography: The Journal of the American Dental Association, 139(3) S7-S13. https://doi.org/10.14219/jada.archive.2008.

Yen, J.C., Chang, F.J., Chang, S., 1995, A new criterion for automatic multilevel thresholding: IEEE Transactions on Image Processing, 4(3), 370-378. https://doi.org/10.1109/83.366472

Zack, G.W., Rogers, W.E., & Latt, S. A., 1977, Automatic measurement of sister cromatid exhange frecuency: Journal of Histochemistry & Cytochemistry, 25(7), 741-753. https://doi.org/10.1177/25.7.70454

Peer Reviewing under the responsibility of Universidad Nacional Autónoma de México.

This is an open access article under the CC BY-NC-SA license(https://creativecommons.org/licenses/by-nc-sa/4.0/)