Boletín de la Sociedad Geológica Mexicana Volumen 75, núm. 3, A150823, 2023 http://dx.doi.org/10.18268/BSGM2023v75n3a150823

Parametrización petrofísica de secuencias siliciclásticas areno-arcillosas con redes neuronales

Petrophysic parametrization of sand-clay siliciclastic sequences with neural networks

Daniel López-Aguirre^1,*, Silvia Raquel García-Benítez², Rubén Nicolás-López^1,3,Enrique Coconi-Morales³

¹ Posgrado Ingeniería en Exploración y Explotación de Recursos Naturales, Facultad de Ingeniería, Universidad Nacional Autónoma de México, Ciudad Universitaria, Coyoacán, 04510, CDMX, México.

² Instituto de Ingeniería, Universidad Nacional Autónoma de México, Ciudad Universitaria, Coyoacán, 04510, CDMX, México.

³ Instituto Mexicano del Petróleo, Eje Central Lázaro Cárdenas Norte 152, Col. San Bartolo Atepehuacan, Gustavo A. Madero, 88630, CDMX, México.

* Autor para correspondencia: (Daniel López-Aguirre) This email address is being protected from spambots. You need JavaScript enabled to view it.

Cómo citar este artículo:

López-Aguirre, D., García-Benítez, S. R., Nicolás-López, R., Coconi-Morales, E., 2023, Parametrización petrofísica de secuencias siliciclásticas areno-arcillosas con redes neuronales: Boletín de la Sociedad Geológica Mexicana, 75 (3), A150823. http://dx.doi.org/10.18268/BSGM2023v75n3a150823

Manuscrito recibido: 16 de Enero de 2023 ; Manuscrito corregido: 12 de Mayo de 2023 ; Manuscrito aceptado: 12 de Junio de 2023.

RESUMEN

En este trabajo se utilizan redes neuronales como una ventajosa herramienta para estimar parámetros petrofísicos de la columna estratigráfica atravesada por varios pozos. Los parámetros porosidad, volúmenes minerales y saturación de agua e hidrocarburos, se obtienen a partir de registros geofísicos de pozo básicos (rayos gamma, resistividad profunda, densidad volumétrica y tiempo de tránsito) y se infieren para otras zonas de la misma área geológica, en los que no se cuenta con este cuadro de información. Este análisis se realizó en secuencias siliciclásticas areno-arcillosas atravesadas por varios pozos perforados para alcanzar un yacimiento de hidrocarburos de baja permeabilidad. Se presentan estimaciones con modelos empíricos para enfrentarlas con las obtenidos con las redes neuronales de forma que se califique la actuación de la alternativa inteligente. Las leyes que rigen la dinámica de los parámetros, así como los detalles del contexto geológico quedan inmersos en los pesos de la red y la consistencia fenomenológica está definida a través de la congruencia de las entradas para conseguir las salidas elegidas. Se muestra la forma en la que el modelo neuronal habilita la propagación confiable de valores de propiedad y se convierte en un ventajoso auxiliar en el estudio de contextos geológicos muy complejos o escasamente parametrizados en los que las condiciones para la aplicación de correlaciones y métodos empíricos, así como el tiempo que se invierte en los procesos de ajuste y contextualización de registros, menguan la calidad y cantidad del conocimiento que se obtiene sobre el medio.

Palabras clave: modelos petrofísicos, registros de pozos, secuencias siliciclásticas, redes neuronales.

ABSTRACT

In this work neural networks are used as an advantageous tool to estimate petrophysical parameters of the stratigraphic column traversed by several wells. The parameters porosity, mineral volumes, and water and hydrocarbon saturation are obtained from basic geophysical well logging (gamma rays, deep resistivity, volumetric density and transit time) and are inferred for other sites, in the same geological area, where they are not measured, so this information matrix is not available. This analysis was performed on sand-clay siliciclastic sequences traversed by several wells drilled to reach a low-permeability hydrocarbon reservoir. Estimates with empirical models are presented to compare them with those obtained with neural networks in order to qualify the performance of the intelligent alternative. The laws that govern the dynamics of the parameters as well as the details of the geological context are immersed in the weights of the network and the phenomenological consistency is defined through the congruence of the inputs to achieve the chosen outputs.The way in which the neural model enables the reliable propagation of property values is shown and becomes an advantageous auxiliary in the study of very complex or poorly parameterized geological contexts in which the conditions for the application of correlations and empirical methods as well as how the time invested in the processes of adjustment and contextualization of records, decreases the quality and quantity of knowledge obtained about the environment.

Keywords: petrophysical mo- dels, well logs, siliciclastic sequences, neural networks.

1. Introducción

El análisis petrofísico a partir de registros geofísicos de pozos es una de las herramientas más importantes en el desarrollo de conocimiento aplicado del subsuelo. La información recuperada de estos registros se emplea durante la perforación y terminación del pozo y en las intervenciones durante su vida útil hasta su abandono. El proceso convencional para la obtención de propiedades petrofísicas implica el uso de varios modelos restringidos por el tipo de litología (siliciclásticos o carbonatos) los cuales, a su vez, se subdividen en otros más específicos (arcillosos-arenosos o carbonatos-dolomías, por citar algunos ejemplos) que constituyen una serie de formulaciones que son como trajes a la medida para cada contexto geológico. Esta dinámica de partición funcional tiene éxito restringido sobre todo en los casos frontera o aquellos que se alejan (así sea ligeramente) de las condiciones de la muestra (litología) que sirvió para el desarrollo de esas ecuaciones. Además, estos modelos precisan de ciertos parámetros que no son siempre económicos o de fácil adquisición (como, por ejemplo, la resistividad del agua (Rw), la resistividad del lodo (Rmf) y el enjarre de lodo (Rmc)).

Otra condición que en ocasiones afecta la estimación de propiedades petrofísicas es la cantidad de curvas de registros que son suficientes para resolver, por ejemplo, la matriz de volúmenes minerales. Para esta solución se requiere que la matriz de m * n sea cuadrada (m=n) por lo que la cantidad de parámetros litológicos que se desean obtener debe ser igual a la cantidad de curvas de entrada con las que se cuenta para realizar el arreglo matricial. Ante la escasez se puede sacrificar el número de salidas (determinar únicamente los principales minerales que forman la roca, por ejemplo) o construir las curvas faltantes con información básica disponible.

Entre los trabajos antecedentes de construcción de modelos petrofísicos con redes neuronales puede mencionarse el de Krug y Ali (2018) quienes utilizaron análisis estadísticos de datos de registros geofísicos de pozo y datos geoquímicos de campos siliciclásticos. Con los registros de rayos gamma, densidad volumétrica y tiempo de tránsito los autores obtienen perfiles acumulativos de minerales arcillosos y carbonatados. Se muestran las capacidades del modelo para obtener litología, sin embargo, no determina saturaciones de fluidos en la roca, lo cual es un objetivo planteado en el presente trabajo. Por su parte, Ba Alawi, et al. (2020) predicen la resistividad, presión capilar y permeabilidad relativa con modelos neuronales a través de la resistividad de núcleos, además obtienen saturaciones de fluidos. Una de las limitantes del trabajo de Alawi, es que sólo es aplicable a bases de datos con análisis de núcleos, situación menos frecuente en los pozos comparada con la asequibilidad de registros geofísicos. Khan et al. (2021) y Al-Sabaa et al. (2021) son trabajos en los que también se presentan modelos inteligentes con las salidas relativas.

La propuesta en este documento es un método robusto que salva las dificultades o carencias de las aplicaciones del tipo porque permite, de forma simple y asequible estimar la porosidad, los volúmenes minerales y la saturación de fluidos. Las redes neuronales pueden ser una herramienta de soporte paramétrico inicial, cuando se modelan datos de registro, en retroalimentación cuando sirven para completar los modelos petrofísicos. En ambas fases un modelo neuronal permite propagar las informaciones a otras áreas o pozos dentro del geo-contexto analizado.

2. Sobre la Inteligencia Artificial y las Redes Neuronales

La inteligencia artificial (IA) es una de las ramas de las ciencias de la computación que se inserta en el estudio del proceso del pensamiento y comportamiento cognitivo humano (Russell y Norvig, 2010). Se intenta que de alguna forma las máquinas sean capaces de percibir, razonar y actuar (Winston, 1992) con la inteligencia que desplegaría una persona (Kurzweil, 1990), es decir, la automatización de la conducta inteligente (Luger y Stubblefield,1993). Las teorías de la IA encuentran un medio para su implementación a través de las computadoras, la programación inteligente es extensa y no funcionaría sin los avances de velocidad de procesamiento y memoria aportados por la industria del cómputo.

La IA utiliza representaciones simbólicas basadas en un número finito de primitivas y de reglas para la manipulación de símbolos, por ejemplo, redes semánticas y lógica de predicados, y también la llamada sub-simbólica, la cual utiliza representaciones numéricas del conocimiento. Este enfoque se caracteriza por crear sistemas con capacidad de aprendizaje imitando al cerebro (redes neuronales), o a la evolución (algoritmos genéticos).

Existe una clasificación de modelos de inteligencia artificial que se basa en el objetivo y la forma en que trabaja el sistema (Russell y Norvig, 2010) (Figura 1):

• Sistemas que piensan como humanos: o modelado cognitivo, basado en teorías de la mente expresadas como un programa computacional. A través de entradas y salidas del programa se emula el funcionamiento de la mente.
• Sistemas que piensan racionalmente: se intenta codificar el “pensamiento correcto”, o proceso de razonamiento. Se construyen programas con líneas del pensamiento que crean sistemas inteligentes.
• Sistemas que actúan racionalmente: se trata con agentes que perciben su ambiente a través de sensores y actúan sobre ese ambiente. Se intenta que operen autónomamente en la creación y persecución de metas.

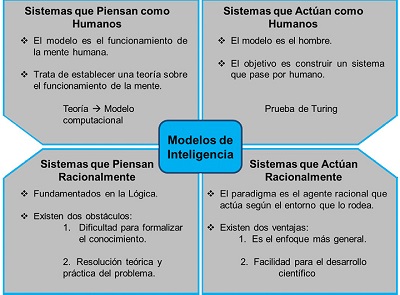Figura 1. Clasificación de los modelos de Inteligencia con base al objetivo y esquema de funcionamiento.

Sobre los intentos por describir aspectos de la inteligencia con máquinas son las redes neuronales RN las que buscan emular el aprendizaje humano (reconocimiento de patrones, memorización y asociación de hechos, entre otros) para resolver problemas donde la expresión de la solución a través de un algoritmo es compleja o imposible. Una RN está compuesta por unidades de procesamiento que habilitan intercambio de información a través de una estructura diseñada para operar haciendo crecer su capacidad de aprender y mejorar su funcionamiento (Matich, 2001).

La analogía entre una neurona biológica y una artificial se muestra en la Figura 2. Se muestran las conexiones entre los nodos (I_1, I_2, …, I_n) que representan las dendritas y los axones (entradas) y la salida (y) sí se referencia a una neurona anterior a la que se está analizando. Los pesos (w_1, w_2, …, w_n) representan la sinapsis y la aproximación umbral representa la actividad realizada por el núcleo de la célula (soma).

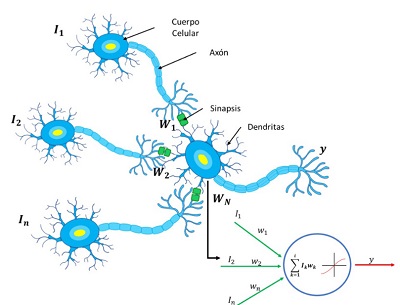Figura 2. Analogía de Neuronas Biológicas con una Neurona Artificial.

Los componentes principales de una red es el conjunto de nodos y las conexiones entre ellos. Los nodos son unidades computacionales que reciben información externa (entradas) la cual es procesada para obtener una respuesta (salida). Las unidades de procesamiento reciben, procesan y transmiten señales tal como las neuronas biológicas.

En la Figura 3 se muestra un esquema de una red neuronal con la representación del flujo de información. La red tiene tres capas: entradas, oculta y salida.

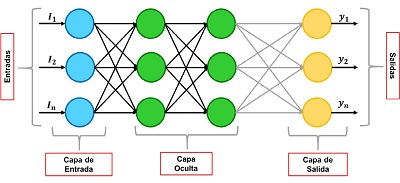Figura 3.Esquema de una RN multicapa, modificada de Matich (2001).

El procesamiento neuronal tiene ventajas de modelado importantes: i) aprendizaje adaptativo, ii) auto-organización, iii) tolerancia a fallos y iv) operaciones en tiempo real. La adaptabilidad se refiere a la capacidad para diferenciar patrones mediante el entrenamiento sin especificar funciones de distribución de probabilidad ni modelos descriptivos específicos. Las redes neuronales emplean su capacidad de aprendizaje adaptativo para autoorganizar la información que reciben durante la operación, siendo “aprender” el concepto que describe la modificación de cada elemento procesal. La generalización en las redes es la facultad para responder apropiadamente cuando se presentan datos o situaciones a las que no habían sido expuestas anteriormente (Hilera y Martínez, 1995).

Comparadas con los sistemas computacionales tradicionales donde estos pierden su funcionalidad cuando sufren un error de memoria, las RN son resilientes ante fallo de neuronas sin caídas o colapsos. Lo anterior se traduce como la capacidad para reconocer patrones con ruido, distorsionados o incompletos (tolerancia a fallos respecto a los datos) y seguir realizando su función (aunque sea destruida parte de la red). Esto porque la información está distribuida en las conexiones con cierto grado de redundancia.

2.1 APRENDIZAJE EN LAS RN

Se conoce como entrenamiento al proceso en el que una red aprende a calcular la salida correcta a partir de los datos de entrada del conjunto ejemplo o conjunto de entrenamiento. Se puede definir al aprendizaje como el proceso en el que se modifican los pesos de la red como respuesta a una información de entrada (modificación, destrucción o creación de conexiones entre neuronas). Existen dos métodos de aprendizaje de gran importancia: a) no supervisado y b) supervisado.

En el caso no supervisado o autoorganizado la red no requiere de un agente externo para realizar el ajuste de sus pesos sinápticos mientras que en el supervisado se requiere de un agente externo o supervisor que sirve para realizar la modificación de los pesos hasta que la salida sea lo bastante aproximada a la considerada correcta.

En esta investigación se usó el algoritmo de aprendizaje supervisado conocido como backpropagation, cuya idea central es que los errores en las capas ocultas son retro-propagadas desde la capa de salida. El método emplea un ciclo que comienza aplicando un patrón como estímulo, éste se propaga hasta generar una salida que se compara con la deseada y se calcula una señal de error. Las salidas de error se propagan hacia atrás hacia todas las neuronas de la capa oculta que contribuyen directamente a la salida. Sin embargo, las neuronas de la capa oculta solo reciben una fracción de la señal total del error, relativa a la contribución a la salida.

El algoritmo busca el conjunto de pesos que genera el valor mínimo de error mediante una técnica conocida como regla del gradiente descendiente o regla delta.

2.2 ETAPAS DEL ENTRENAMIENTO

Las etapas del algoritmo de retro-propagación son:

• Etapa 0: Se inicializan los pesos como un conjunto de valores aleatorios.
• Etapa 1: Mientras la condición “parar” sea falsa, se deben realizar los pasos 2 a 9 aquí nombrados.
• Etapa 2: Para cada par de entrenamiento, ejecutar las etapas 3 a 8.
• Etapa 3 (feedforward): Para cada unidad de entrada (ᵡ_i,→ i = 1,2,3,...,n), recibe una señal ᵡ_i y se envía esta señal a todas las unidades de la capa siguiente (unidades de la capa oculta).
• Etapa 4: Cada unidad oculta a_inj,→ j = 1,2,3,...,m) suma los pesos de las señales de entrada o realiza la operación correspondiente según la función de entrada escogida.

a_inj = net_inj = Σⁿ_i=1 ᵡ_i w_ij, (1)

se aplica la función de activación para el cálculo de la señal de salida como

a_j = f (net_inj), (2)

y se envía la señal a todas las unidades de la capa siguiente.

• Etapa 5: Suma de cada unidad de salida (y_k,→ k = 1,2,3,...,l) con los pesos en la señal de entrada,

y_ink = net_k = Σ^m_j=1 a_j w_j,k, (3)

aplicando la función de activación se obtiene la señal de salida,

y_k = f (y_ink ), (4)

• Etapa 6 (retro propagación del error): Cada unidad de salida (y_k,=1,2,3,...,l) recibe el valor deseado correspondiente al patrón de entrenamiento, para el cálculo del error:

δ_k = (zk - ak) f´ (y_ink ), (5)

con este valor se puede calcular el término de corrección de peso (usado para actualizar el peso w_j,k ).

• Etapa 7: Cada unidad oculta (a_j,→ j = 1,2,3,...,m) suma a la entrada delta,

δ_inj =. Σ^l_k=1 δ_kw_j,k, (6)

multiplicando por la derivada de la función de activación para calcular el error, para las j-ésimas unidades ocultas,

δ_j = δ_inj f ´(a_inj). (7)

• Etapa 8 (actualización de pesos): Para cada unidad de salida (y_k,→ k = 1,2,3,...,l) se deberá actualizar su correspondiente peso. La regla de cambio de pesos para la capa de salida es la siguiente:

w_j,k (Nuevo) = w_j,k (Anterior) + Δw_j,k , (8)

donde

Δw_j,k= ηδ_ka_j

Ahora, para realizar la actualización de los pesos en las unidades de entrada a una unidad oculta, se procede a hacer el siguiente cálculo:

w_j,k (Nuevo) = w_j,k (Anterior) + Δw_i,j , (9)

donde

Δw_i,j= ηδ_ja_j

• Etapa 9: Restablecer la condición de inicio.

3. Presentación de la base de datos: caso de estudio

El estudio se desarrolló en formaciones sobreyacentes a un campo productor de hidrocarburos en horizontes areno-arcillosos (siliciclásticos) de aproximadamente 250 km² de extensión el cual puede ser catalogado como campo petrolero de tamaño grande. Los registros geofísicos básicos de 16 pozos que constituyen la base de datos se muestran en planta en la Figura 4.

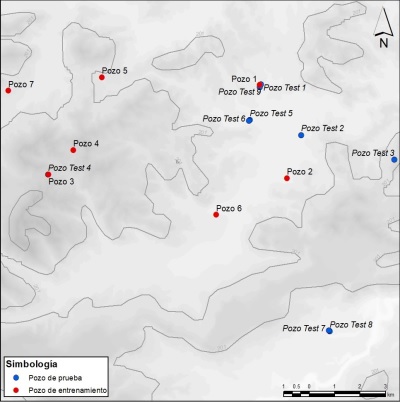Figura 4. Detalle de los pozos ubicados en el área de estudio, que se encuentran entre las coordenadas 22°00’00”S y 114°00’00”E.

Para distinguir entre patrones de comportamiento y dirigir las búsquedas paramétricas para la particular distribución espacial de la información petrofísica, se definieron las siguientes tres formaciones geológicas (a partir del registro de Rayos Gamma, información común en los pozos seleccionados):

• Formación A → Formación de Sobrecarga, oscila entre los 300 y 800 [m], de profundidad, compuesta de litologías areno-arcillosas con contenido de hidrocarburos gaseosos. En el área de estudio esta formación representa un intervalo de recursos prospectivos-contingentes (que no se ha desarrollado por diversos factores) y es apartada del análisis principal pues no está presenta en todos los pozos.
• Formación B → Esta formación geológica representa el sello regional de los yacimientos subyacentes a ella, toda vez que está compuesta de minerales arcillosos. El interés de analizar esta formación es por su génesis y las implicaciones sobre las características únicas del yacimiento, lo que pone a prueba las capacidades de generalización de las redes neuronales para determinar litologías y estado de fluidos.
• Formación C → Esta formación tiene propiedades litológicas que derivan de la presencia de secuencias arenosas y arcillosas (diferentes espesores) con una distribución espacial asociada al origen turbidítico que generan abanicos submarinos al pie del talud, en donde también se presentó erosión generada por la corriente de turbidez. El contacto inferior de esta formación geológica es discordante con secuencias carbonatadas del Cretácico, evidenciado por secuencias de brecha de diferentes espesores. En esta investigación se atiende el efecto de este contacto, pero está fuera del espacio acotado por los pozos analizados.

Es importante reiterar que esta formación geológica contiene intervalos arenosos y arcillosos y que estos últimos representan sellos locales (además del sello regional que es la Formación B). Ambos constituyen trampas que contienen fluidos hidrocarburos, sin embargo, en este trabajo se analizan los efectos que podrían generar la presencia de hidrocarburos en trampas finitas en la emulación del modelo petrofísico.

De los registros geofísicos en la base de datos, siete fueron separados para el entrenamiento y nueve para la prueba de la red (Tabla 1). Las variables de entrada son cinco curvas de registros por pozo (ordenada por un contador Z, pseudoprofundidad), en dos formaciones geológicas cortadas por todos los pozos: el yacimiento C y la formación que le sobreyace B: a) Profundidad (depth), b) Rayos Gamma (GR), c) Tiempo de Transito (DT), d) Densidad volumétrica (RHOB) y e) Velocidad Compresional (VP).

Tabla 1. Descripción de los datos utilizados en RN.

4. Descripción de la Metodología

La metodología empleada en el presente trabajo implica, primero, obtener las propiedades petrofísicas porosidad, volumen de cada mineral, saturación de agua y saturación de hidrocarburos para los siete pozos de entrenamiento con una resolución de 0.1524 m. El conjunto de prueba seleccionado asegura que las examinaciones a la red avalan el mismo nivel de funcionamiento con entradas distintas a las que usaron en el entrenamiento, es decir, lo que da confianza sobre su modo de trabajo al tiempo que evita la sobre-especialización (comportamiento óptimo únicamente con los ejemplos de entrenamiento y errores considerables en casos no vistos). Después de estas etapas se calculan para los nueve pozos las propiedades petrofísicas con métodos convencionales de forma que se puedan comparar con las obtenidas con el modelo neuronal. En la Figura 5 se presenta un diagrama de flujo sobre los pasos descritos en los párrafos anteriores.

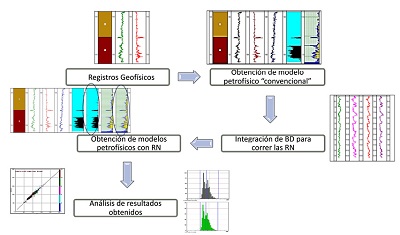Figura 5.Diagrama de flujo de la metodología propuesta.

5. Resultados Obtenidos

La distribución de datos de entrenamiento y prueba se considera adecuada para controlar la evolución de los modelos y para generar su validación. Debe mencionarse que la resolución vertical (en Z) en entrenamiento es de 0.1524 m mientras que, para los datos de prueba, se obtienen resultados cada 2 m.

Una vez definidos los modelos litológicos y la saturación de fluidos en los siete pozos de entrenamiento, se utiliza este arreglo neuronal para predecir los volúmenes litológicos de los nueve pozos de prueba. Los resultados son muy alentadores si se calculan las correlaciones y se observa la congruencia entre los valores neuronales, las curvas de porosidad, saturación y volúmenes de minerales y sus correspondientes calculadas con métodos convencionales utilizados en la industria.

Los resultados de la porosidad total (Por y Por_Red) (carril 4, obtenidas con petrofísica curva color morado y con redes curva negra punteada), saturación de fluidos obtenida con petrofísica (Sat; carril 5), saturación de fluidos obtenida con redes ( Sat_Red carril 6), volúmenes mineralógicos determinados con petrofísica ( Vclay y Vsand ; carril 7) y con redes ( Vclay_R y Vsand_R; carril 8); para tres pozos de entrenamiento (pozos 1,4 y 6), más cinco pozos de prueba (pozos 2, 3, 6, 8 y 9) se muestran en las Figuras 6-13.

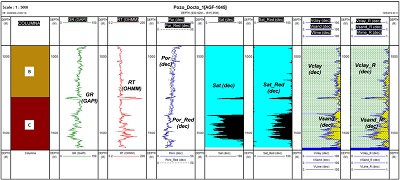Figura 6.Resultados de porosidad (carril 4), saturación (carriles 5 y 6) y mineralogía (carriles 7 y 8), del pozo 1 de entrenamiento.

Los resultados del pozo 1 (entrenamiento) (Figura 6) guardan una alta correlación entre métodos para la porosidad y la saturación en la zona de hidrocarburos siendo un poco más baja la estimación con el método convencional. En cuanto a la mineralogía se identifica el máximo porcentaje de litología de arenas (cuarzo) en la zona de hidrocarburos (roca almacén) y una disminución hacia la cima del yacimiento, manteniéndose en un porcentaje mínimo en todo el sello (zona de arcillas).

Por lo que respecta a los resultados para el pozo 4 (Figura 7) se obtuvieron resultados similares a los obtenidos para el pozo 1. Este caso es influenciado por la determinación petrofísica convencional, la zona de alta presencia de cuarzo e hidrocarburos, se extiende algunos metros sobre la base del sello, lo que invita a reconsiderar su cima determinada inicialmente con el análisis cualitativo del GR. Por otro lado, en el pozo 6 se obtuvieron resultados muy similares, es decir, las estimaciones están muy próximas para las curvas de porosidad y fracciones minerales obtenidas (con ambos métodos). En cuanto a la curva de saturación de hidrocarburos lo identificado con las redes neuronales resulta ser más certero (en contexto con lo obtenido para los otros pozos, zona punteada), que lo calculado con el modelo convencional en cuya estimación se observa una incipiente saturación de hidrocarburos en toda la columna geológica incluyendo el sello regional (Formación B), lo cual es poco factible a partir de los resultados de los otros pozos del área.

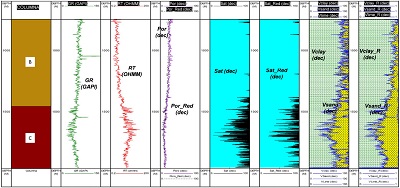Figura 7.Resultados de porosidad (carril 4), saturación (carriles 5 y 6) y mineralogía (carriles 7 y 8), del pozo 4 de entrenamiento.

Hasta este punto se han explicado los comportamientos sobre datos de entrenamiento, siendo más atractivo el tipo de resultados obtenidos para las pruebas, como el pozo 2 (Figura 9). En este caso los valores fueron obtenidos sin el soporte de aproximaciones petrofísicas (obtenidas con métodos convencionales) y fueron congruentes (espacialmente) con lo definido para el pozo 6 (Figura 8), definiendo con claridad la zona de yacimiento en los tracks asociados a la mineralogía y saturaciones (zona punteada Figura 9). De manera independiente se obtuvo el modelo petrofísico convencional siendo evidente que hay disparidad en la saturación respecto de los resultados de otros pozos (condición que es identificada con la red neuronal).

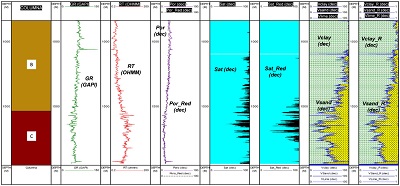Figura 8.Resultados de porosidad (carril 4), saturación (carriles 5 y 6) correlación errática y mineralogía (carriles 7 y 8), del pozo 6 de entrenamiento.

Para los pozos 3 y 6 de prueba con la red neuronal se obtuvieron resultados adecuados para el contexto geológico y consistentes con lo obtenido con el método convencional, sobre todo para la estimación de saturación de hidrocarburos.

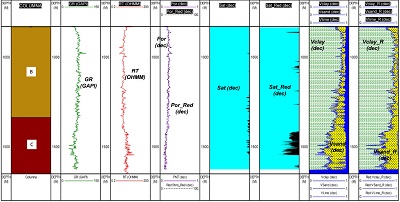Figura 9.Resultados de porosidad (carril 4), saturación (carriles 5 y 6) muy errática y mineralogía (carriles 7 y 8), del pozo 2 de prueba.

Finalmente, la litología para los pozos 8 y 9 de prueba, se determinó con ambas metodologías, pero son las redes neuronales la que generaron una mejor discretización de los paquetes arenosos en el yacimiento. Para la saturación de fluidos, como ocurrió en los casos anteriores, es más específica con redes ya que la presencia de hidrocarburos se acota en su mayoría al yacimiento tanto para el pozo 8 de prueba, como para el pozo 9 de prueba (área punteada).

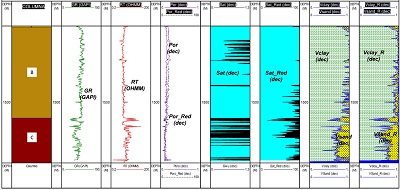Figura 10.Resultados de porosidad (carril 4), saturación (carriles 5 y 6) errática y mineralogía (carriles 7 y 8), del pozo 3 de prueba, muestran buena correlación.

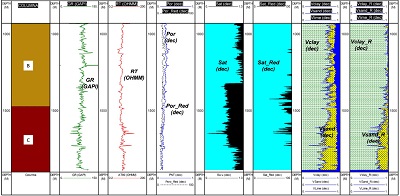Figura 11.Resultados de porosidad (carril 4), saturación (carriles 5 y 6) errática y mineralogía (carriles 7 y 8), del pozo 6 de prueba.

Figura 12.Resultados de porosidad (carril 4), saturación (carriles 5 y 6) y mineralogía (carriles 7 y 8), del pozo 8 de prueba.

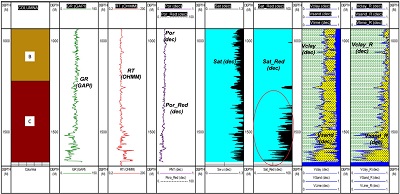Figura 13.Resultados de porosidad (carril 4), saturación (carriles 5 y 6) errática y mineralogía (carriles 7 y 8), del pozo 9 de prueba.

6. Discusión de resultados obtenidos

Mediante modelos petrofísicos convencionales y redes neuronales se obtuvieron valores de porosidad total, saturación de hidrocarburos y las fracciones minerales de los siete pozos de entrenamiento y nueve pozos de prueba, obteniendo resultados muy aceptables con la alternativa inteligente en las curvas de porosidad que presentan buena correlación entre curvas obtenidas con uno y otro método, incluso para pozos de prueba en los que la obtención del parámetro es mediante la propagación del trabajo de la topología neuronal.

Por su parte, respecto a la saturación de hidrocarburos, este fue el parámetro obtenido con redes neuronales que mejor sustento encontró con la configuración geológica (se destaca mediante una elipse de línea punteada negra para los casos en los que se obtuvo una mejor aproximación). Las redes permiten obtener valores de saturaciones más homogéneos entre pozos (en entrenamiento y prueba) que confirman la presencia de hidrocarburos hacia la cima de la Formación C, sin que los resultados se vieran alterados por lo reconocido sobre saturación de fluidos con modelos petrofísicos (entre los pozos de entrenamiento estos valores divergen).

Finalmente, para las fracciones minerales se obtuvieron resultados con buena correlación entre la definición con modelos convencionales implementando el proceso de inversión petrofísica básica y los resultados de petrofísica obtenidos con redes neuronales, lo cual refleja la alta capacidad de los modelos inteligentes para ser usados en la propagación de parámetros hacia zonas de interés que cuenten con información escasa o parcialmente definida.

7. Conclusiones

El método y el trabajo con redes neuronales para determinar el modelo petrofísico fue aplicado a pozos de entrenamiento y pozos con condiciones similares (prueba), para estos últimos el modelo petrofísico convencional fue obtenido de manera independiente. El enfrentamiento de los resultados permite concluir que el comportamiento del modelo inteligente fue satisfactorio y, se considera, puede extenderse a la estimación de otros parámetros de interés petrolero.

Se obtuvieron curvas de porosidad, saturación de agua e hidrocarburos, así como las fracciones mineralógicas predominantes de 16 pozos (siete de entrenamiento y nueve de prueba), con una muy alta correlación respecto de los resultados obtenidos con modelos convencionales.

Se observó que los resultados obtenidos con redes neuronales adquirieron mayor estabilidad pozo a pozo si se comparan con los obtenidos con correlaciones disponibles en la literatura, cuya calidad de salida está sujeta a la experiencia del usuario. De esto se desprende que la técnica, mediante el entrenamiento adecuado aún sobre un número reducido de pozos, puede aplicarse en extrapolación hacia otros pozos y áreas con características similares. Es decir, integrando un modelo petrofísico 1D para cada pozo, o pseudopozo, se pueden construir modelos tridimensionales (3D), como un entramado de los 1D, de forma que en cualquier punto del espacio se consigan valores ponderados de porosidad, saturación, volúmenes mineralógicos, entre otros, con un relativamente alto nivel de confianza.

Contribución de los autores

Conceptualización: Silvia R. García-Benítez, Daniel López-Aguirre; Análisis o adquisición de datos: Rubén Nicolás-López, Daniel López-Aguirre; Desarrollo metodológico: Silvia R. García-Benítez, Enrique Coconi-Morales, Daniel López-Aguirre; Redacción del manuscrito Original: Daniel López-Aguirre; Redacción del manuscrito corregido y editado: Silvia R. García-Benítez; Diseño gráfico: Daniel López-Aguirre; Interpretación: Silvia R. García-Benítez, Rubén Nicolás-López, Enrique Coconi-Morales, Daniel López-Aguirre.

Financiamiento

No se precisó de financiamiento para la elaboración de este trabajo.

Agradecimientos

Se agradece a los coautores por sus aportaciones y valiosas críticas al presente trabajo. A las instituciones que otorgaron apoyo con medios e información para la integración de la base de datos empleada.

Conflictos de intereses

Los autores declaran no tener algún conflicto de intereses.

Referencias

Al-Sabba, A., Gamal, H., Elkatatny, S., 2021, Generation of a complete profile for porosity log while drilling complex lithology by employing the artificial intelligence, en SPE Symposium: Artificial Intelligence - Towards a Resilient and Efficient Energy Industry, Virtual: Arabia Saudita, King Fahd University of Petroleum and Minerals, SPE-208642-MS. https://doi.org/10.2118/208642-MS

Ba Alawi, M., Gharbi, S., Mahmoud, M., 2020, Modeling and prediction of resistivity, capillary pressure and relative permeability using artificial neural network, en International Petroleum Technology Conference: Dhahran, Kingdom of Saudi Arabia, IPTC-19854-MS. https://doi.org/10.2523/IPTC-19854-MS

Hilera, J., Martínez, V.,1995, Redes neuronales artificiales: fundamentos, modelos y aplicaciones. Volumen 87895 de Serie Paradigma: España, RA-MA, 390p.

Khan, M.R., Kalam, S., Abbasi, A., 2021, Integrating pore geometrical characteristics for permeability prediction of tight carbonates utilizing artificial intelligence, en Abu Dhabi International Petroleum Exhibition y Conference: Abu Dhabi, Schulumberger, SPE-208005-MS. https://doi.org/10.2118/208005-MS

Krief, M., Garat, J., Stellingwerff, J., Ventre, J.,1990, A petrophysical interpretation using the velocities of P and S waves (full-waveform sonic): The Log Analyst, 31(6), 355-369.

Krug, R., Ali, H., 2018, Integration of petrophysical data análisis and optimization for Use in Artificial Intelligence Neural Networks, en SEG International Exposition and 88th Annual Meeting: USA, Society of Exploration Geophysicists, 2157-2160. https://doi.org/10.1190/segam2018-2997932.1

Kurzweil, R., 1990, The age of intelligent machines: Cambridge, MIT Press, 580p.

López-Aguirre, D., 2008, Origen, evolución e importancia económica petrolera de la cuenca de Chicontepec: México, Universidad Nacional Autónoma de México, Tesis de Licenciatura, 111p.

López-Aguirre, D., 2016, Geomecánica para formaciones siliciclásticas, mediante análisis de sistemas petroleros y compresibilidades: México, Universidad Nacional Autónoma de México, Tesis de Maestría, 307p.

Luger, G.F., Stubblefield, W.A., 1993, Artificial intelligence: Structures and strategies for complex problem solving: California, Benjamin/Cummings Publishing Company, 740p.

Matich, D. J., 2001, Redes neuronales: Conceptos básicos y aplicaciones: Argentina, Universidad Tecnológica Nacional, Facultad Regional Rosario, 55p.

Mavko, G., Mukerji, T., Dvorkin, J., 2003, The rock physics handbook, Second edition: UK, Cambridge University Press, 511p. https://doi.org/10.1017/CBO9780511626753

Nicolás-Lopez, R., Valdiviezo-Mijangos, O.C., 2016, Rock physics templates for integrated analysis of shales considering their mineralogy, organic matter, and pore fluids: Journal of Petroleum Science and Engineering,137, 33- 41. https://doi.org/10.1016/j.petrol.2015.11.009

Pickett, G.R.,1963, Acoustic character logs and their applications in formation evaluation: Journal of Petroleum Technologies, 15, 650–667. https://doi.org/10.2118/452-PA

Ramos, H., Zinat, D., Ramírez, T., 2008, Registros geofísicos en México: Tabasco, México Schlumberger Offshore Services, 316 p.

Russell, S., Norvig, P., 2010, Artificial intelligence: A modern approach, 3rd Edition: Upper Saddle River, Prentice-Hall, 1132p.

Santillán, N., Aguayo, J.E., 2011, Facies sedimentarias turbidíticas del Terciario Inferior en la Cuenca de Chicontepec, Centro-Oriente de México: Ingeniería Investigación y Tecnología, 12(3), 337-352.

Wang, J., Cao, J., Zhao, S., Qi, Q., 2022, S-wave velocity inversion and prediction using a deep hybrid neural network: Science China Earth Science, 65, 724–741. https://doi.org/10.1007/s11430-021-9870-8

Winston, P.H., 1992, Artificial Intelligence: USA, Addison-Wesley Publishing, 737 p.

Anexo

PROPIEDADES PETROFÍSICAS CON EL MÉTODO CONVENCIONAL

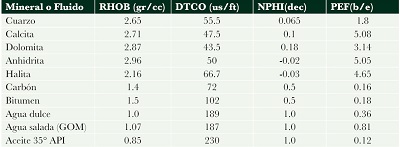
El método convencional para obtener el modelo petrofísico del medio continúo atravesado por el pozo, de acuerdo a la literatura se basa en resolver con un sistema de ecuaciones en el que las variables desconocidas son la porosidad y los “n” minerales formadores de roca que se considere se tienen en el área de estudio. En este método es fundamental conocer igual número de registros que tipos de litologías presentes en la roca. Por ejemplo, si se consideren las siguientes matrices de roca: sílice, calcita, dolomita y arcilla, será necesariamente requerido contar con registros que brinden información litológica, como pueden ser: porosidad neutrón (NPHI), densidad volumétrica (RHOB), tiempo de tránsito (DTCO) y factor fotoeléctrico (PEF); por decir algunos. En caso de no contar con algún registro de los antes citados, es posible intercambiar alguno de ellos por algún parámetro obtenido de los otros registros, como, por ejemplo, el volumen de arcilla.

Para el caso que se cita, el sistema de ecuaciones es el siguiente:

ϕ_N= ϕϕ_Nf +V₁ ϕ_N1+V₂ ϕ_N2+V₃ ϕ_N3+V₄ ϕ_N4…(A2.1)

ρ_b=ϕ ρ_f+ V₁ρ₁+ V₂ρ₂+ V₃ρ₃+ V₄ρ₄…… (A2.2)

DT=ϕDT_f+V₁DT₁+V₂DT₂+V₃DT₃+V₄DT₄…… (A2.3)

V_SH=ϕ V_SHf + V₁V_SH1+ V₂V_SH2+ V₃V_SH3+ V₄V_SH4 (A2.4)

1=ϕ + V₁+ V₂+ V₃+ V₄…… (A2.5)

Donde:

φ_N, es el valor leído del registro de Porosidad Neutrón (NPHI).

ρ_b, es el valor leído del registro de Densidad volumétrica (RHOB).

DT, es el valor leído del registro de Tiempo de Tránsito compresional o primario (DTCO).

V_SH, es el valor leído del registro sintético de Volumen de Arcilla.

φ, es la porosidad total del medio.

V₁, a V₄, son los minerales formadores de roca, presentes en la litología de análisis. Son las variables incógnitas del sistema.

Tabla A2.1. Valores de referencia de principales minerales y fluidos del subsuelo (Ramos, 2008).

Del sistema de ecuaciones anterior, se obtiene el siguiente arreglo matricial:

Donde:

La primera matriz (5 * 1), de la izquierda son las lecturas directas de los registros involucrados en el punto de interés.

La segunda matriz (5 * 5), son valores de respuesta a los registros geofísicos conocidos para el fluido como para cada uno de los minerales considerados en el análisis (Tabla A2.1).

La tercera matriz (5 * 1), de la derecha, son las incógnitas que se busca discretizar.

El sistema de ecuaciones tiene solución, ya que tenemos 5 incógnitas y 5 ecuaciones, que al tener los datos de referencia e invirtiendo la matriz de 5 * 5, así como multiplicándola por la matriz 5 * 1 de los valores leídos de los registros, es posible obtener los parámetros petrofísicos de las fracciones de los minerales y la porosidad del sistema de roca analizado.

La revisión por pares es responsabilidad de la Universidad Nacional Autónoma de México.

Este es un artículo Open Access bajo la licencia CC Y-NC-SA (https://creativecommons.org/licenses/by-nc-sa/4.0/)