BOLETÍN DE LA SOCIEDAD GEOLÓGICA MEXICANA Vol 56, Núm. 1, 2003, p. 1-9 http://dx.doi.org/10.18268/BSGM2003v56n1a1

Estimación de densidades, distribuciones de longitud y longitud total de fracturas; un caso de estudio en la Falla de Los Planes, La Paz, B.C.S.

Ángel Francisco Nieto-Samaniego^1,*, Susana A. Alaniz-Álvarez¹, Gustavo Tolson², Shunshan Xu¹ y J. Antonio Pérez-Venzor³

¹ Centro de Geociencias, Universidad Nacional Autónoma de México, Campus Juriquilla, Apdo. Postal 1-742, 76001 Querétaro, Qro., México.
² Instituto de Geología, Universidad Nacional Autónoma de México, Apdo. Postal 70-296, 04510 México, D. F., México.
³ Departamento de Geología Marina, Universidad Autónoma de Baja California Sur, Apdo. Postal 19-B, La Paz, B.C.S., 23080, México.

* This email address is being protected from spambots. You need JavaScript enabled to view it.

Resumen

Con el fin de conocer el límite máximo de fracturas que puede contener un cuerpo de roca así como la manera en que están distribuidas sus longitudes, se estudiaron las fracturas en el Granito Las Cruces, usando fotografías con campos visuales horizontales de ca. 10, 1 y 0.1 m. Los parámetros analizados fueron longitud total de fractura (L=ΣLi), intensidad de fractura (I=ΣLi/A), densidad de fractura [D=(1/A)Σ(Li/2)²], el exponente de la longitud de fractura acumulada (C) y la dimensión de caja de las trazas de fractura Cb. En nuestro análisis, juntando las tres escalas, los parámetros L e I muestran variación con exponentes de ca. 0.6 y -0.4 respectivamente, mostrando que las escalas ca. 1 y 0.1 m fueron preferidas para la generación de fracturas. Adicionalmente, en cada escala I muestra una gran dispersión, reflejando que existen diferentes grados de fracturamiento en los lugares de muestreo. El parámetro D elimina el efecto del área; se observa que sus valores permanecen siempre menores que 3, aún para las muestras más fracturadas, sugiriendo la existencia de un límite máximo en la densidad de fractura. Tanto el exponente de la longitud de fractura acumulada C, como la dimensión de caja Cb, muestran valores inferiores a 1.87, sugiriendo también un valor límite. Al utilizar nuestros datos para calcular la longitud total de fractura contenida en una imagen de escala 10 m surge la necesidad de realizar un análisis multiescalar, ya que utilizando una sola escala la estimación de longitud total de fractura fue 31 veces menor.

Palabras clave: fractales, fractura, densidad de fractura, longitud de fractura.

Abstract

In order to know if there is an upper limit for the amount of fractures contained in a rock mass, we studied fracture arrays in the Las Cruces Granite using photographs covering horizontal lengths of ca. 10, 1 y 0.1 m. We analyzed the following parameters: total length (L=ΣLi), intensity (I=ΣLi/A), density [D=(1/A)Σ(Li/2)²], the exponent of cumulative length (C), and the Box dimension (Cb).

Parameters L and I show a variation with exponent ca. 0.6 and ca. -0.4 respectively, indicating that scales 1 and 0.1 m were preferred for fracture formation. In addition, within each scale interval there is a large dispersion of I indicating different degrees of fracturing in the sampling sites.

The parameter D eliminates the effect of area; and its value is consistently below 3 over three orders of magnitude in fracture length. We interpret this behavior as indicative of the existence of an upper limit for fracture density. Cumulative length C and Box dimensions Cb show values below 1.87, also suggesting that there is a limiting value. We used our data for calculating the total fracture length in an image of ca. 10 m scale. The analysis shows that we need a multi-scalar treatment; using a single scale the result was underestimated by a factor of 31.

Key words: fractals, fractures, fracture density, fracture length.

1. Introducción

Tanto en sistemas de fracturas naturales, como en sistemas generados por modelado numérico, se ha observado que los conjuntos de fracturas adquieren una característica fundamental al evolucionar: la repetición de los objetos en distintas escalas (e.g., Cowie et al., 1995; Gupta y Sholz, 2000). Cuando esto ocurre, el objeto ha adquirido una geometría fractal. Por ejemplo, el número de fracturas de una longitud (o intervalo de longitudes), puede variar de manera tal, que al observar imágenes del objeto a escalas distintas, las imágenes son similares para el observador, o más estrictamente, son equivalentes desde un punto de vista estadístico sin importar la escala de observación (Figura 1). Esta característica se observa comúnmente en la distribución de longitudes acumuladas de fallas o fracturas, habiéndose encontrado que obedecen relaciones de potencia o exponenciales (e.g., Ackermann et al., 2001).

Una relación del tipo ley de potencia le confiere al parámetro analizado, longitud en este caso, una geometría autosimilar, lo que significa que el objeto se repite sin distorsiones en las distintas escalas. Al obedecer una ley de potencia, la distribución de tamaños no tiene tendencia hacia un valor característico, o sea que se comporta de la misma manera en todo el rango de escalas mientras la relación de potencia se conserve. Ese rango de escalas acota los límites de su comportamiento fractal.

Se han realizado numerosos estudios usando distintas técnicas para estimar la distribución de longitudes; comúnmente se usa una imagen sobre la cual se miden directamente las longitudes de las fallas o fracturas, o bien, se aplica un conteo de cajas. La información que se recupera de esta manera presenta un sesgo en las escalas mayores y menores, debido a la pérdida de resolución o a muestreo incompleto (e.g., Pickering et al., 1995).

Por otra parte, el grado de fracturamiento de una roca ha sido analizado utilizando distintos parámetros, siendo el más general la cantidad de fractura medida como longitud de trazas, dividido entre el área donde fueron medidas. Una observación por demás interesante es que, en estudios realizados en casos naturales, se ha observado la existencia

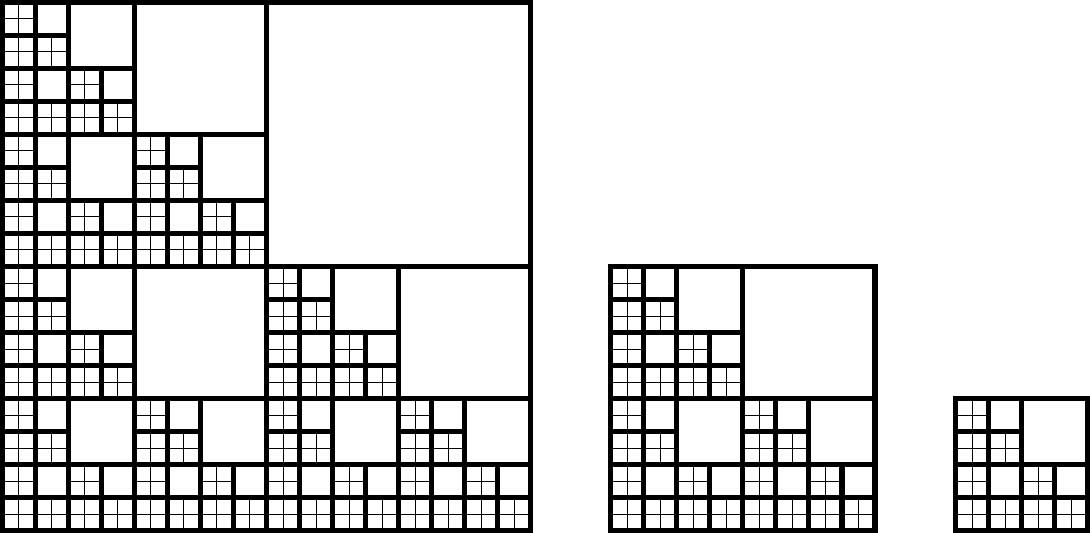
Figura 1. Modelo de un objeto fractal (modelo de Sammis), que ilustra la autosimilaridad. Obsérvese que los cuadros menores son réplicas del cuadro mayor y si no se tiene una escala de referencia, no es posible determinar la escala de la observación.

de un valor máximo del grado de fracturamiento (Renshaw, 1997; Gupta y Scholz, 2000). Sin embargo, las estimaciones del comportamiento en las densidades de fracturas o la distribución de longitudes basados en este tipo de análisis presentan problemas importantes en el muestreo. En el trabajo presentado por Renshaw (1997) se utilizaron mapas e imágenes obtenidas de la literatura cubriendo 14 órdenes de magnitud de escala, pero los mapas difícilmente son representativos de la cantidad de fallas o fracturas de una región, ya que son elaborados con muy distintos criterios y con las omisiones impuestas por la falta de afloramientos. En el otro caso, Gupta y Scholz (2000) utilizaron un modelo digital de elevación cubriendo un área muy extensa. A partir del análisis con fotografías convencionales que presentamos en este trabajo, consideramos que la resolución de los modelos digitales de elevación está muy lejos de ser adecuada para este tipo de estudios. No obstante lo anterior, nuestro trabajo indica también la presencia de un límite máximo de densidad de fractura de manera consistente con esos dos estudios.

En este trabajo presentamos algunos resultados del estudio realizado en el Granito Las Cruces, ubicado en La Paz, Baja California Sur, México, el cual es cortado por la Falla de Los Planes. Esta falla es una estructura mayor, con más de 70 km de longitud y varias etapas de actividad (Fletcher et al., 2000). Las distintas etapas están evidenciadas por la presencia de varias familias de fallas sobrepuestas. Algunas de esas familias de fallas, que muestran ángulos de inclinación moderados, están relacionadas con pseudotaquilitas y pequeñas bandas miloníticas, mientras que las de ángulos más altos sólo presentan brechas o cataclasitas. Estudiamos la distribución de longitudes de fracturas y establecimos su naturaleza autosimilar. Basados en nuestras mediciones, discutimos la posibilidad de obtener una única dimensión fractal para la Falla de Los Planes. Por último, presentamos un ejemplo de su uso para hacer extrapolaciones hacia escalas mayores o menores a aquellas donde es posible la observación directa.

2. Metodología

Con el fin de maximizar la calidad de los datos, se procuró encontrar afloramientos ideales. Nos concentramos en arroyos perpendiculares a la traza de la falla de los Planes, eligiendo aquellos cuyos afloramientos estuvieran libres de vegetación, con un mínimo de intemperismo y donde se observaran planos de fallas. Las zonas seleccionadas fueron aquellas en las que se observó un grado de fracturamiento de intenso a moderado. En esos afloramientos se procedió a tomar fotografías con campos visuales que permitieran cubrir, en la horizontal, una longitud de ca. 10, 1, 0.1 m (Figura 2). Siempre las fotografías de escalas menores estuvieron incluidas en el campo visual de la fotografía de escala mayor. Adicionalmente, se tomó una muestra orientada, de la cual se elaboró una lámina delgada y se procedió a tomar fotomicrografías de escalas 0.01 y 0.001 m, siguiendo los mismos criterios que en las escalas mayores.

Se eligieron 15 afloramientos en total, tomándose tres fotografías en cada uno de ellos (escalas 10, 1, 0.1 m) con excepción de un afloramiento, donde se tomaron tres fotografías con longitudes horizontales de 1 y 0.1 m en puntos distintos dentro de la fotografía de escala 10 m. De esta manera, se utilizaron un total de 48 imágenes de campo y dos fotomicrografías.

En un papel transparente colocado sobre las fotos se trazaron manualmente las fracturas que se pudieron observar con claridad y se procedió a medir la longitud de cada una de ellas (Figura 3). Con los datos de longitudes, se calcularon los parámetros siguientes:

-La longitud total de fractura (L=ΣLi).

-La intensidad de fractura (I=ΣLi/A).

-La densidad de fractura [D=(1/A)Σ(Li/2)²].

-El exponente (C) de la línea de tendencia obtenida

para las gráficas de longitud acumulada.

-La dimensión de caja (Cb).

Siendo A el área de la imagen y Li la longitud de cada fractura.

Figura 2. Ejemplo de las fotografias tomadas en campo y microscopio para este estudio. Cada fotografía fue tomada dentro de la que abarca la mayor área. Nótese que en cada imagen aparece, indicada con unrectángulo, el área que cubre la fotografía de acercamiento siguiente.

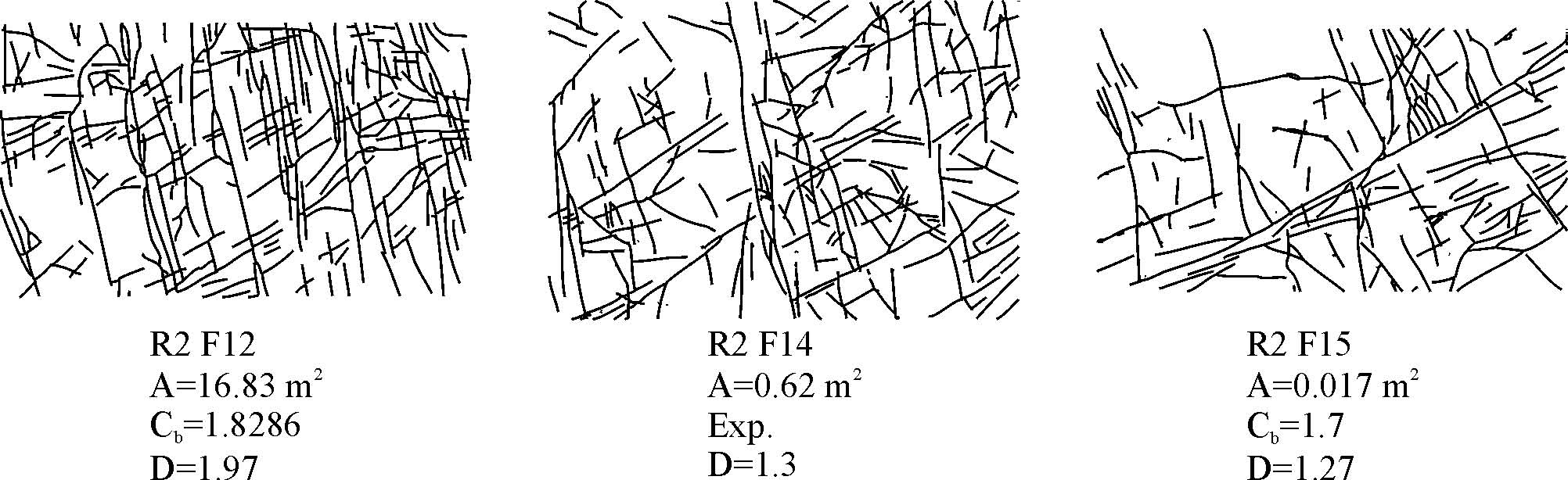
Figura 3. Ejemplo de trazas de fractura. En cada caso se trazaron manualmente cada una de las trazas de fractura usando papel transparente colocado sobre la fotografía. Las trazas se midieron manualmente y se calcularon los parámetros indicados. A= área de la imagen; Cb = dimensión de caja; D = densidad de las fracturas; Exp. indica que la curva acumulativa de longitudes de trazas se ajusta a una función exponencial. 

3. Resultados e interpretación

La longitud total de fractura (L) correspondiente a cada fotografía fue graficada contra el área en un espacio logarítmico (Figura 4a). La línea de tendencia se ajustó a una relación de potencia de exponente ca. 0.6. La Intensidad de fractura, definida como la longitud de fractura por unidad de área, presenta un comportamiento inverso al de L. La línea de tendencia obtenida se ajusta a una relación de potencia con exponente de -0.4 (Figura 4b).

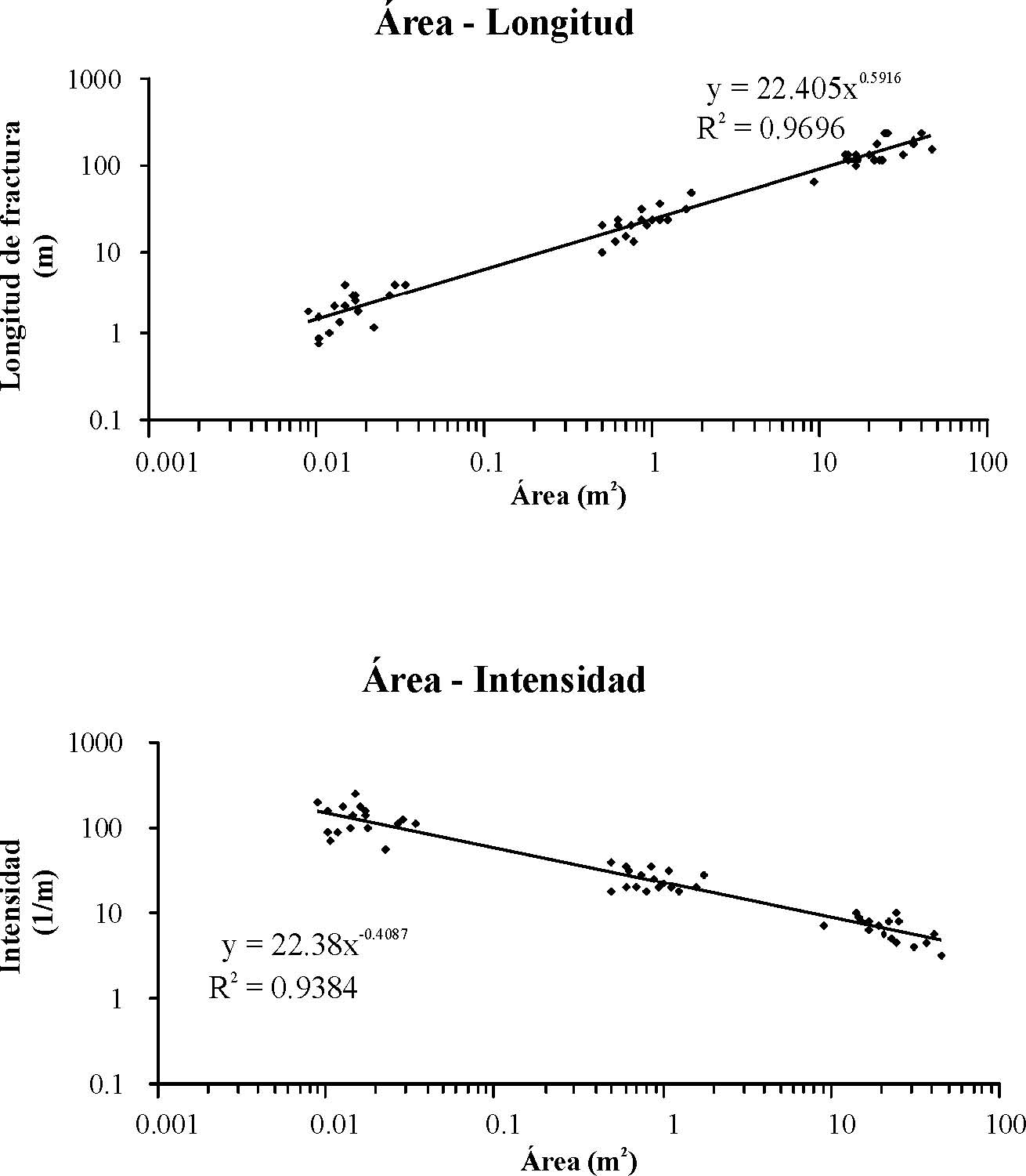
Figura 4. a) Gráfica en espacio logaritmico de longitud total de fractura contra área. b) Gráfica en espacio logarítmico de Intensidad de fractura contra área.

Si consideramos un patrón de fracturas que se repite exactamente a sí mismo en diferentes escalas, y si medimos exclusivamente las fracturas que corresponden a una escala específica para calcular la longitud total, entonces la intensidad variará siguiendo una ley de potencia con exponente de -0.5, lo cual refleja el cambio de área en las escalas (Figura 5). El valor (-0.4) obtenido en nuestros datos, indica que hay una mayor cantidad de fractura en las fotografías más grandes, que aquella esperada si el patrón de fracturas se repitiera exactamente en todas las escalas. De esta manera, deducimos que además del cambio de área, hay otros factores que modifican la pendiente en la gráfica de intensidad contra área.

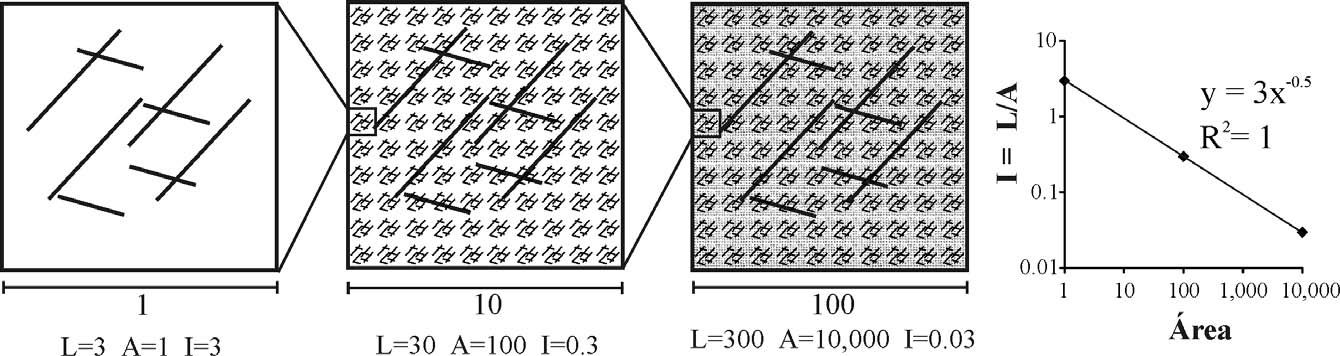
Figura 5. Modelo que muestra la variación de la longitud total de la fractura y la intensidad de fractura al variar la escala de medición. El modelo está formado por la repetición exacta, en tamaños más grandes, del arreglo de fracturas mostrado en el dibujo de la izquierda. En cada caso, se midieron exclusivamente las fracturas que corresponden a cada escala. La gráfica de la derecha muestra que la variación del área produce una pendiente de 0.5 en la intensidad de fracturamiento.

Al graficar la intensidad de fractura separadamente para cada una de las escalas estudiadas, se observa que no existe una tendencia (Figura 6), por el contrario, hay una dispersión grande en los valores de I. Si consideramos válido asumir que la longitud total de fractura es directamente proporcional a la cantidad de deformación, entonces esa dispersión indica que los lugares de muestreo representan diferentes estados en la evolución del fracturamiento de la roca. El comportamiento observado en I sugiere que los tamaños de fractura entre 0.01 y 1 m fueron preferidos durante el desarrollo del sistema. Los datos sugieren también la existencia de un límite máximo de I para cada escala.

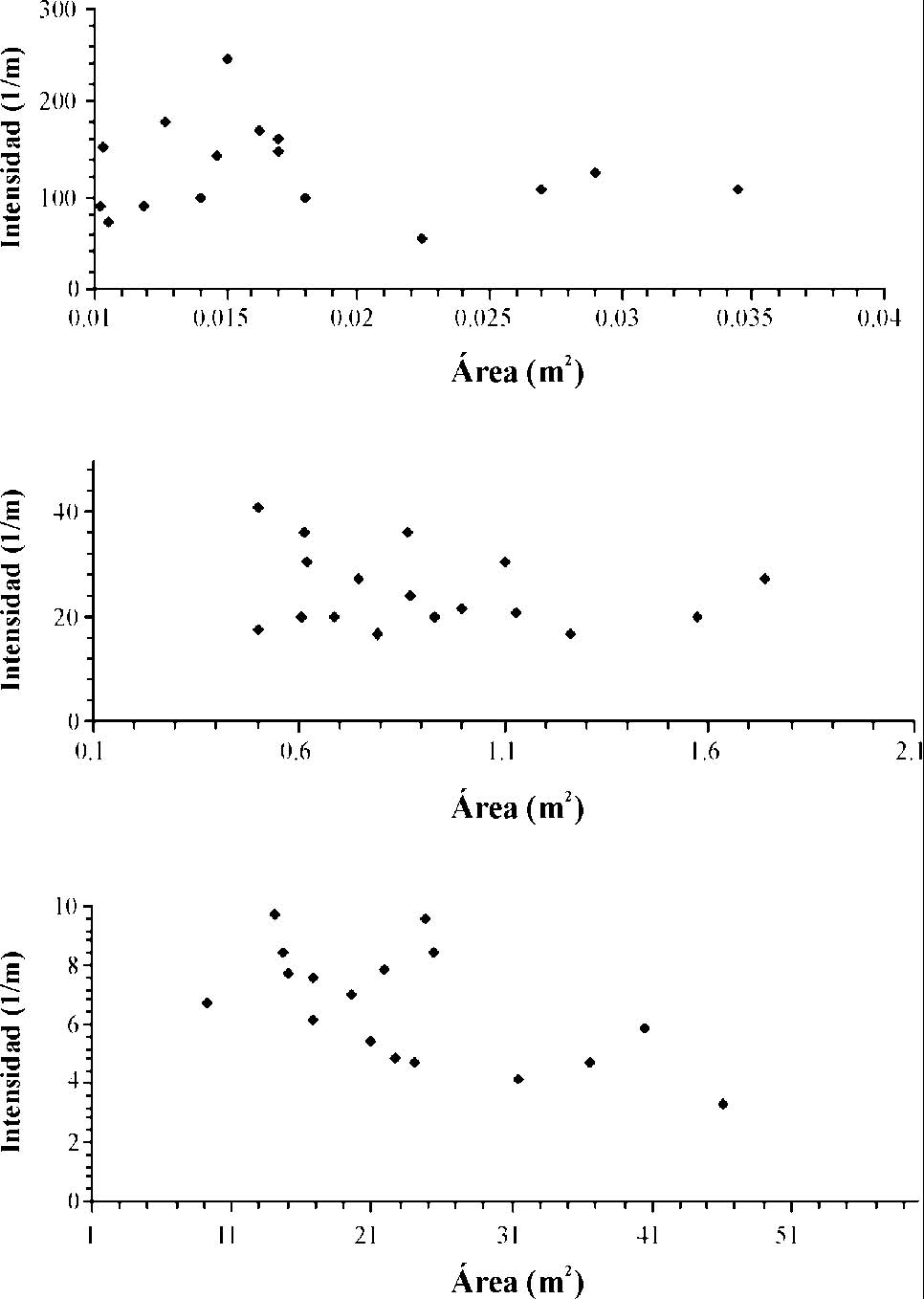Figura 6. Gráfica de Intensidad de fractura contra área, para cada escala
por separado

La densidad de fracturas elimina el efecto del cambio de área (Figura 7). Se observa una ligera tendencia a tener valores menores en las escalas pequeñas, mientras que hacia las escalas grandes no se observa tendencia a incrementarse. Parece probable una tendencia asintótica a la horizontal, sugiriendo la existencia de un valor máximo, que en este caso es igual a 3. Esta observación es consistente con las conclusiones de Renshaw (1997), quien analizó trazas de fracturas cubriendo 14 órdenes de magnitud en longitud y encontró un valor máximo para las densidades igual a 2 y valores ligeramente menores para las longitudes pequeñas. El hecho que la deformación se concentre a lo largo de las fallas grandes significa que las fallas más pequeñas son abandonadas paulatinamente durante el proceso de deformación. Entonces en las escalas pequeñas observaremos fracturas y fallas que acomodaron una deformación menor. Bajo este supuesto, el aumento progresivo de la densidad de fractura hacia las escalas mayores que se observa en la Figura 7, es el registro del incremento en la magnitud de la deformación acomodada durante la evolución del sistema de fracturas. La relación menor deformación – menor densidad de fractura, con una evolución hacia un valor constante al aumentar la magnitud de la deformación, ya había sido propuesta (Gupta y Scholz, 2000). El valor absoluto de la máxima densidad de fracturas no es tan relevante como su existencia, ya que el valor máximo probablemente dependa de la litología, entre otros factores, y posiblemente nunca sea alcanzado.

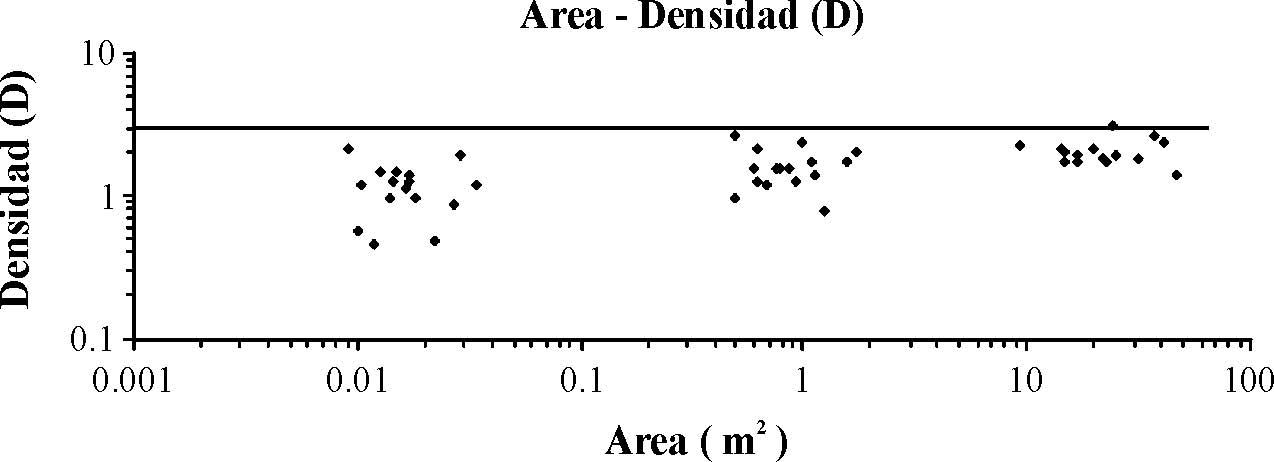
Figura 7. Gráfica en espacio logarítmico de densidad de fractura contra área.

Las gráficas de longitud acumulada se ajustan a una relación del tipo ley de potencia para las partes centrales de las gráficas. El exponente C muestra una dispersión grande para los datos individuales de cada fotografía. Los valores varían entre 0.66 y 2.22. Sin embargo, al reunir las tres fotografías que corresponden a un solo afloramiento en una misma gráfica, realizando la corrección por área, los valores de C se ubican entre 1.51 y 1.91. Estas observaciones tienen sentido solamente si la densidad de fractura en una escala es homogénea en el área de la escala mayor. Esta situación parece ser válida en el caso analizado, tanto por la consistencia de los valores obtenidos, como debido a que todos los muestreos se hicieron dentro de las zonas de falla, donde el granito se observó fracturado en toda el área de muestreo. Considerando las fotografías restantes después de eliminar aquellos casos que se ajustan mejor a una distribución exponencial, observamos que con excepción de uno, todos los valores son menores que 1.87 (Figura 8).

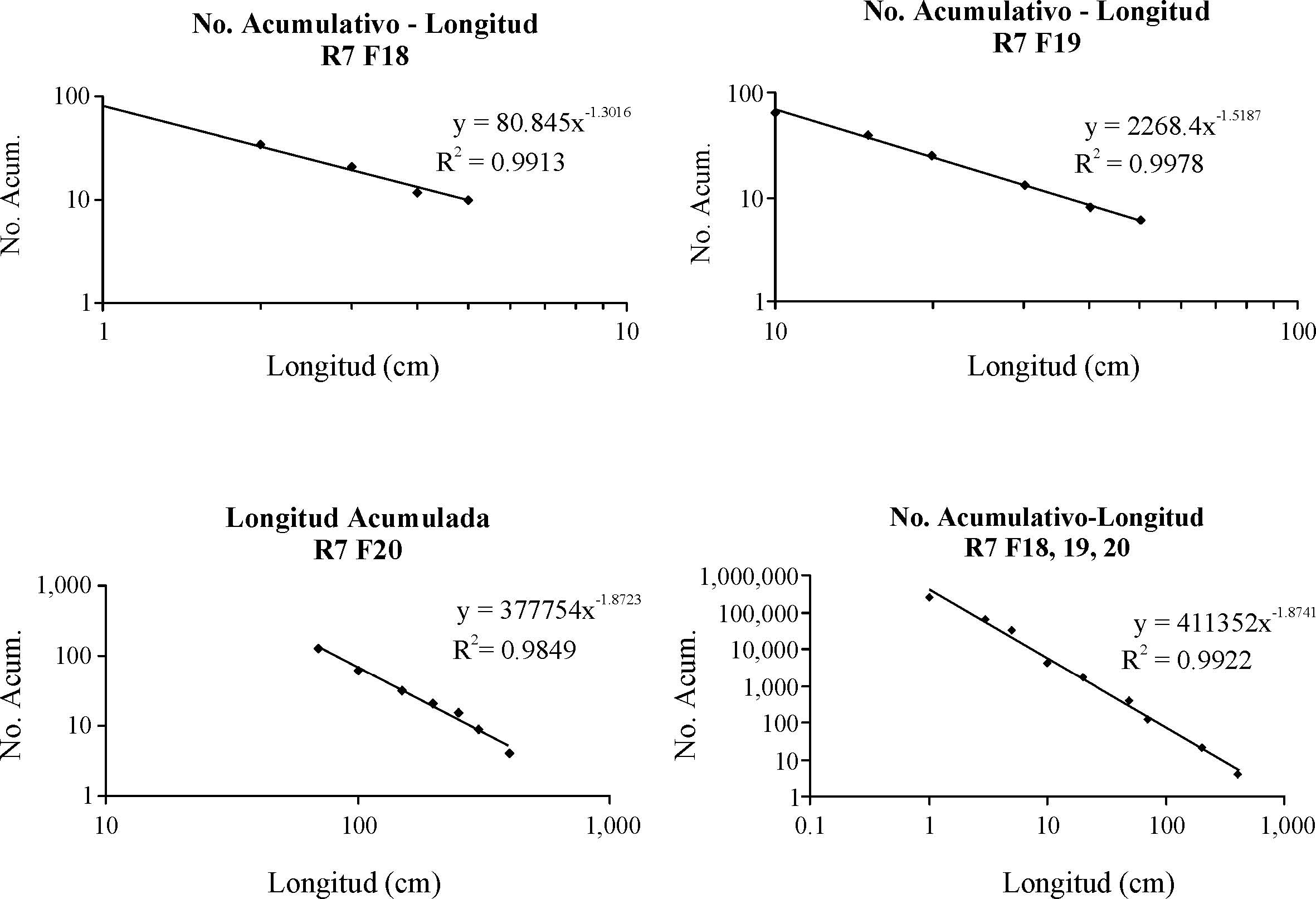
Figura 8. Curvas de longitud de fractura acumulada para las fotografías R7F20, R7F19 y R7F18.

Los conteos de cajas se realizaron sobre imágenes digitalizadas en blanco y negro de las trazas de fracturas dibujadas manualmente. Se utilizó el programa denominado Fractal Analysis (Tolson, 2001), el cual utiliza el método Box-Flex descrito en Barton (1995). Esos conteos muestran una variación pequeña del exponente Cb, observándose como valor máximo 1.87 (Figura 9), al igual que en las longitudes acumuladas.

 
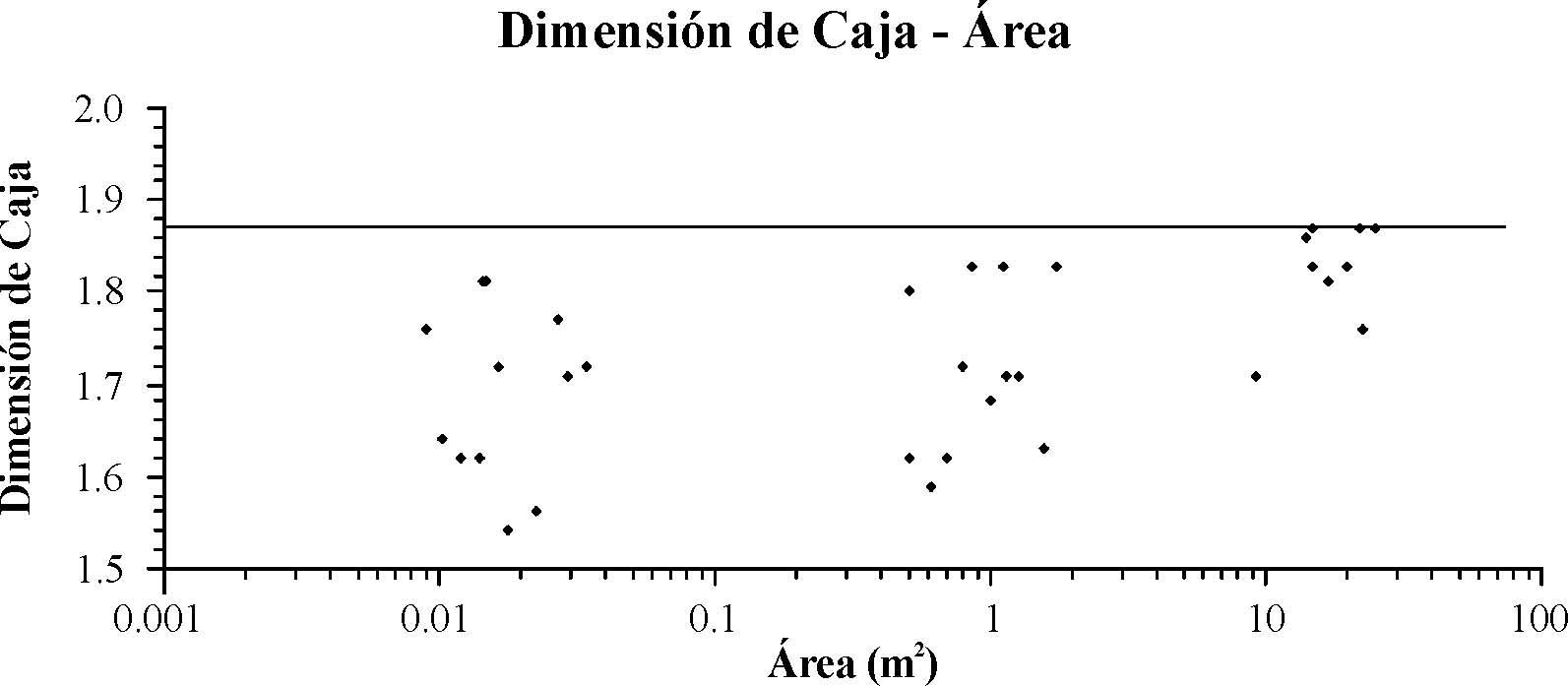
Figura 9. Gráfica en espacio logarítmico de dimensión de caja contra área.

4. Autosimilaridad y longitud total de fractura

Un fractal autosimilar es un objeto que se mantiene invariante en distintas escalas y/o en distintos puntos del espacio. Esta característica puede ser definida de manera precisa matemáticamente (e.g., Feder, 1988). En un sentido práctico, la autosimilaridad permite que, conociendo el comportamiento del objeto en una escala, podamos extrapolar a una escala distinta. En el caso de las longitudes de fractura, conociendo la distribución de longitudes en una escala podemos determinar la longitud en otra o todas las escalas en las cuales el objeto presenta autosimilaridad, incluyendo aquellas escalas que no podemos observar o medir por ser demasiado pequeñas o demasiado grandes.

En la Figura 8 presentamos las longitudes acumuladas de fractura de las fotografías R7F20, R7F19 y R7F18. Los campos visuales abarcan en la horizontal ca. 10, 1 y 0.1 m, respectivamente.

Ahora compararemos la longitud total de fractura que existe en la fotografía R7F19, con la longitud total de fractura que predice la fotografía R7F20 para un área igual a la que cubre la fotografía R7F19. Considérese que al observar la fotografía con escala de 10 m, no es posible observar las fracturas que aparecen en la escala de 1 m y menos aún en la fotografía de escala 0.1 m. Sin embargo, es posible calcular la longitud total de fractura, la cual nos permite hacer una estimación del volumen que pudiera ser contenido por el enrejado de fracturas.

Para calcular la longitud total de fracturas contenidas en la escala 10 m, utilizamos los valores de k y C de la ecuación que aparece en la gráfica R7F20 (Figura 8), en la ecuación deducida por Scholz y Cowie (1990) (Apéndice A),

El cálculo se hizo usando k = 377754, C = 1.8723 para el intervalo 0.4 a 4.0 m, el cual corresponde a los tamaños de fractura observables a esa escala, y obtuvimos una L de ~281 m. Sin embargo, en esa escala de observación es imposible estimar el incremento de L aportado por las fracturas que aparecen en las fotografías de mayor acercamiento. Ahora, integrando la función para las tres escalas (Figura 8), la cual podemos considerar como nuestra mejor aproximación, obtenemos ~8,770 m de longitud total de fractura, para el intervalo de 0.01 hasta 4 metros. Este resultado es aproximadamente 31 veces la estimación originalmente hecha midiendo lo que se observa en la fotografía R7F20. Este ejercicio ilustra la necesidad de realizar de manera multiescalar los análisis en conjuntos de fracturas, para lograr mejores estimaciones.

5. Conclusiones

Las principales conclusiones que se desprenden de este trabajo son:

1) Las distribuciones de longitud total e intensidad de fractura indican que nuestras muestras contienen zonas con distintos grados de fracturamiento y la densidad de fractura indica que existe un valor máximo, al cual se tiende al aumentar la magnitud de la deformación.

2) La distribución de longitud acumulada de fracturas es un fractal estadísticamente autosimilar. Se considera que el valor de 1.87 para el exponente C constituye también un valor límite para el conjunto de fracturas analizadas.

3) La autosimilaridad de la distribución de longitudes permite utilizar los valores de C obtenidos en nuestro análisis para estimar la longitud total de fractura, incluyendo aquellas escalas que no son observables. En el ejemplo presentado, el análisis en una sola escala estimó únicamente ca. 5% de la longitud total de fractura calculada usando las tres escalas.

Agradecimientos

Se agradece a Crescencio Garduño y Tomás Vázquez, quienes se hicieron cargo de la elaboración de láminas delgadas orientadas; a los estudiantes de geología de La UABCS en La Paz que participaron en los trabajos de campo: Gonzalo Arredondo, Efraín Pérez, Joel Rochín, Fabiola Núñez y Antonio del Rosal. Se agradece también al Ing. Javier Arellano y al M.C. Carlos Pacheco por sus comentarios y sugerencias. Esta investigación fue financiada por el proyecto PAPIIT-IN113399.

Referencias bibliográficas

Ackermann, R.V., Schlische, R.W., Withjack, M.O., 2001, The geometric and statistical evolution of normal fault systems; an experimental study of the effects of mechanical layer thickness on scaling laws: Journal of Structural Geology, 23, 1803-1819.

Barton, C.C., 1995. Fractal analysis of scaling and spatial clustering of fractures, en Barton, C.C., LaPointe, P.R. (eds.), Fractals in Earth Sciences: Plenum Press, New York, 141-177.

Cowie, P.A., Sornette, D., Vanneste, C, 1995. Multifractal scaling properties of a growing fault population: Geophysical Journal International, 122, 457-469.

Feder, J., 1988, Fractals: New York, Plenum Press, 283p.

Fletcher, J.M., Kohn, B.P., Foster, D.A., Gleadow, A.J.W., 2000, Heterogeneous Neogene cooling and exhumation of the Los Cabos block, southern Baja California: evidence from fission-track thermochronology: Geology, 28, 107-110.

Gupta, A., Scholz, C.H, 2000, Brittle regime transition in the Afar depression; implications for fault growth and seafloor spreading: Geology, 28, 1087-1090.

Pickering, G., Bull, J.M., Sanderson, D.J., 1995, Sampling power-law distributions: Tectonophysics, 248, 1-20.

Renshaw, C.E., 1997, Mechanical controls on the spatial density of opening-mode fracture networks: Geology, 25, 923-926.

Sholz, C.H., Cowie, P.A. 1990, Determination of total strain from faulting using slip measurements: Nature, 346, 837-839.

Tolson, G., 2001, Fractal Analysis; software de acceso libre para el cálculo de dimensión de cajas en fracturas: http://geologia.igeolcu.unam.mx /Tolson/Gtolson.htm

Manuscrito recibido: Octubre 3, 2002 Manuscrito corregido recibido: Enero 13, 2003 Manuscrito aceptado: Enero 15, 2003

Apéndice “A”

Deducción de la ecuación para obtener la longitud total de fractura, a partir de la gráfica Longitud – Número Acumulativo de fracturas.

Partiendo de la construcción de la gráfica de número acumulado de fracturas contra longitud, mostrada en la Figura A1, deducimos que el número acumulado de fracturas de una longitud determinada está definido por,

y que el número de fracturas de una longitud determinada es

Asumiendo que la ecuación (A1) es una función continua, hacemos infinitesimales los incrementos en el número y la longitud con el fin de generalizar

Por otra parte, la longitud total aportada por las fracturas de una longitud específica se obtiene al multiplicar dicha longitud por el número de fracturas, así

y la longitud total de un intervalo de longitudes está dada por la integral de esa función,

Las líneas de tendencia obtenidas para los números acumulados de fracturas tienen la forma N(l)=kl^-c; usando esta nomenclatura obtenemos

que es la ecuación utilizada en el texto.

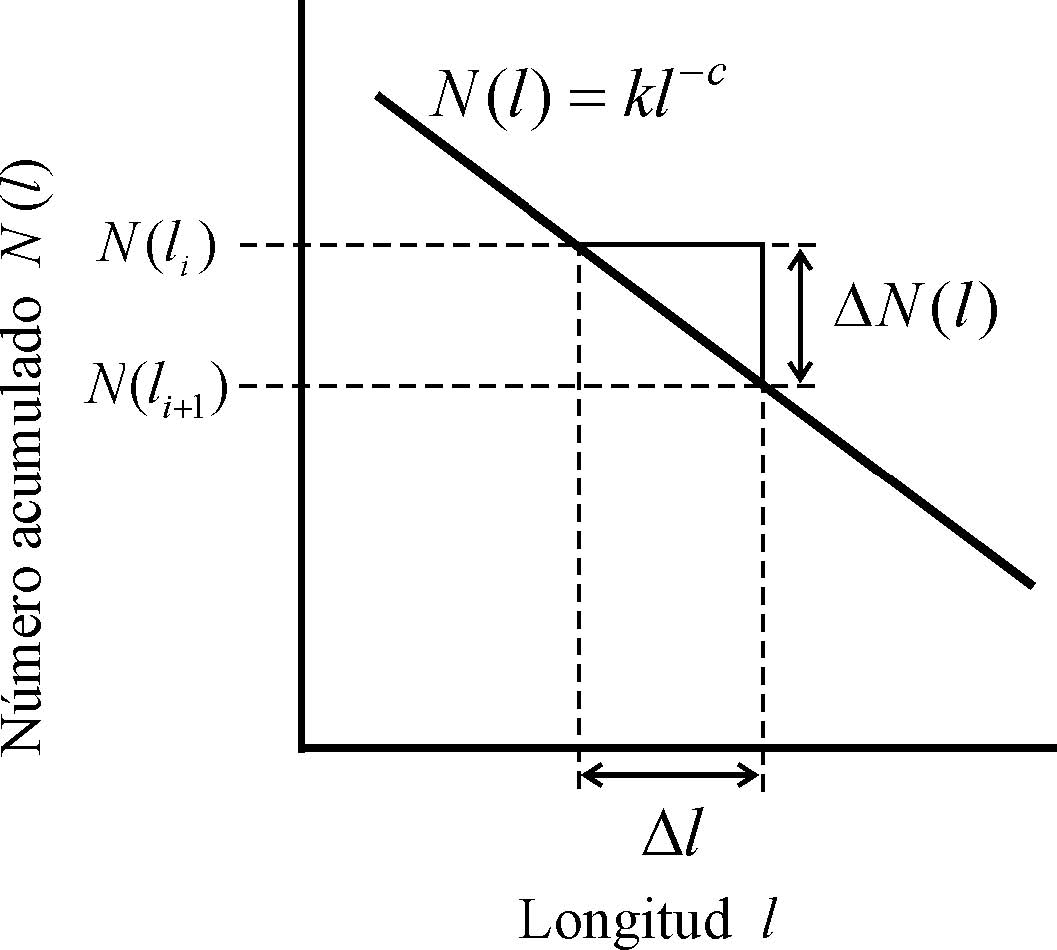
Figura A-1. Esquema que muestra la construcción de una curva de frecuencia acumulada vs. longitud.