|
BOLETÍN DE LA SOCIEDAD GEOLÓGICA MEXICANA http://dx.doi.org/10.18268/BSGM2009v61n3a3 |
 |
Modelo teórico para el cálculo de las solubilidades mutuas entre gases no–polares y agua con sales disueltas. Parte 1: Desarrollo de ecuaciones termodinámicas
Theoretical model to calculate mutual solubilities between non–polar gases and brines. Part 1: Development of thermodynamic equations
Renee J. Pérez1, Robert A. Heidemann2, Eduardo González–Partida3
1ExxonMobil Upstream Research Company 3120 Buffalo Speedway, Houston, TX 77098.
2 Department of Chemical and Petroleum Engineering, University of Calgary, 2500 University Drive Calgary, Alberta, Canada T2N1N4.
3 Centro de Geociencias, Universidad Nacional Autónoma de México, Campus Juriquilla, Boulevard Juriquilla 3001, 76230 Juriquilla, Querétaro, México.
* This email address is being protected from spambots. You need JavaScript enabled to view it..
Resumen
En el presente artículo se propone un modelo teórico para el cálculo del equilibrio químico de fases entre gases no–polares y agua. Este modelo es aplicable completamente a sistemas acuosos puros o con sales disueltas. En ambos casos el modelo proporciona predicciones válidas hasta 647 K, presiones de hasta 2 kilo–bares, y concentraciones de sales disueltas iguales a la saturación del sólido mineral. El modelo termodinámico hace uso de una ecuación de estado para reproducir datos experimentales en todas las fases excepto en la fase líquida del agua. Para esta última se utiliza la constante de Henry. En el caso de la presencia de sales, el potencial químico del soluto gas en la fase líquida del agua está relacionada al potencial químico del soluto en la salmuera a través del coeficiente de Setschenov. Estos coeficientes se pueden derivar de datos experimentales de solubilidad. Con el modelo se pueden reproducir todos los fenómenos de solubilidad cruciales, incluyendo el equilibrio entre tres fases. Sin embargo con las ecuaciones propuestas no se pueden reproducir los fenómenos gas–gas que ocurren en la vecindad del punto crítico del agua ni el equilibrio sólido–liquido que ocurre en los hidratos.
Palabras clave: Gases, salmueras, solubilidad, termodinámica, agua.
Abstract
We propose a thermodynamic model for the equilibrium of non–polar gases, water and aqueous sodium chloride solutions valid to high pressures, high temperatures, and to high ionic strength solutions. The model couples Henry's Law and an equation of state to reproduce experimental data in the aqueous phase and the gas–rich fuid phases. The standard state chemical potential of the solute in brines is related to the standard state chemical potential of the solute in pure water through a salting–out or Setschenov coefficient. The salting–out coeffcients are obtained from experimental data. The model reproduces all crucial phenomena, including three phase equilibrium, at temperatures below the critical temperature of water. The modeling approach cannot account for gas–gas equilibrium phenomena that occur in the vicinity of the water critical point, nor for the hydrate–vapor–liquid equilibrium near the melting point of water.
Key words: Gases, brines, solubility, thermodynamics, water.
1. Introduction
El entendimiento del equilibrio termodinámico de sistemas que contienen salmueras y gases es muy útil tanto desde una perspectiva teórica como desde una perspectiva práctica. Desde el punto de vista teórico, conocer la solubilidad de los gases en el agua y en soluciones electrolíticas facilita la investigación de las propiedades del solvente y de las interacciones entre los electrolitos disueltos y los gases (Wilhem et al., 1977; Smith y Kennedy, 1983). Adicionalmente, modelos termodinámicos de equilibrio vapor–liquido, tales como los que se presentan en este trabajo, permiten realizar estimaciones indirectas de las propiedades calorimétricas y volumétricas de soluciones que contienen pequeñas concentraciones de gases no–polares, las cuales son muy difíciles de medir experimentalmente (Dohanyosonova et al., 2004). Desde el punto de vista práctico, la geoquímica aplicada utiliza datos de equilibrio de fases liquido–vapor para predecir el transporte y destino de los gases que en ocasiones actúan como agentes contaminantes del ambiente. Para la geoquímica del petróleo es importante conocer la distribución de gases entre las fases acuosas y orgánicas para reducir al mínimo su presencia en afluentes acuosos sobre de yacimientos someros de petróleo y, de la misma manera, para predecir el grado de interacción roca/fluido en el subsuelo. Otro problema práctico importante en todos los estudios geoquímicos de los fluidos en el subsuelo es la valoración del pH in situ y de la presión parcial o fugacidad de los gases en solución. Sin una comprensión matemática/termodinámica sólida de la distribución de todos los componentes gaseosos (incluyendo los gases no–reactivos) entre las fases del vapor y el líquido, los cálculos de las características de la salmuera estarían incompletos.
Aparte de la presencia de gases en campos petrolíferos y geotermales (Katz et al., 1959; Cody y Hutcheon, 1994; Hunt, 1996), hay evidencia de gases disueltos en descargas naturales de aceite a lo largo de la costa de California (Hunt, 1996) y en depósitos de carbón (Kotarba y Rice, 2001; Huang et al., 2004) Los gases son componentes importantes en los esquemas termoquímicos de procesos de reducción del sulfato que ocurren en la presencia de electrólitos en la corteza terrestre (Yang et al., 2001). También se han reportado gases y están normalmente presentes en las inclusiones fuidas atrapadas en los minerales autigénicos (Burrus, 2003), y han sido reportados en los fluidos y vapores de fumarolas que emanan de pozos geotermales (Chiodini y Marini, 1998). Dada la importancia de los gases en la naturaleza, y que experimentalmente se ha determinado que la introducción de electrolitos dentro de mezclas gases–agua afecta el equilibrio de fases (Morrison y Billett, 1952), hay una necesidad imperante de construir modelos termodinámicos internamente consistentes, capaces de reproducir valores de solubilidad y del equilibrio composicional en sistemas multifásicos, con o sin electrolitos disueltos, sobre un rango amplio de presión y temperatura.
2. Rango P–T–X del modelo propuesto
Las predicciones y el funcionamiento del modelo de la solubilidad de gases presentado en este trabajo son óptimos para rangos de presión entre 1 y 2000 bares, temperaturas entre 273 y 600 K, y concentraciones de cloruro de sodio acuoso entre 0 y 6 molal. En el sistema NaCl–agua, la concentración del NaCl es igual a la fuerza iónica de la solución (Anderson y Crerar, 1993), de modo que el modelo presentado es también válido para soluciones con fuerza iónica de hasta 6 molal.
Por otro lado, las presiones y las temperaturas en las cuales los algunos gases forman hidratos son bien conocidas (Sloan, 1998). La figura 1 presenta la línea de equilibrio sólido (hidrato)–líquido–vapor para el sistema metano–agua. Existen curvas similares para los sistemas etano–agua, propano–agua, H2S–agua, NH3–agua, butano–agua, y algunos otros gases. Esta curva de equilibrio se desplazan en dirección de la fecha (figura 1) y cambia su pendiente con la adición de cloruro de sodio u otras sales disueltas en agua (Sloan, 1998). No obstante, para cualquier lugar geométrico en el plano dado, el espacio de presión y temperatura presente en la región superior izquierda de la línea de la figura 1 involucra la presencia una fase sólida. Así, las predicciones de la solubilidad vapor–liquido de nuestro modelo en esa área del gráfico se referirán a fases meta–estables. Por el contrario, las predicciones en el espacio presente en la parte inferior derecha de la curva de equilibrio corresponderán a fases estables o a las fases con la energía libre de Gibbs más baja (Carroll, 1992). Los detalles de las técnicas para calcular la estabilidad de las fases para un cálculo dado se presentan más adelante en el texto.
La única limitación de nuestro modelo es que el fenómeno de equilibrio gas–gas que ocurre cerca y más allá de la temperatura crítica del solvente, 647 K en caso del agua, es inaccesible. El comportamiento crítico de mezclas de gases–NaCl–agua, y en un grado inferior, de gases–CaCl–agua, a 800 K y 2500 bares pueden ser encontrados en otros estudios (Krader y Frank, 1985) y en la serie de datos de solubilidad compilados por la IUPAC (International Union of Pure and Applied Chemistry) en los volúmenes 9, 10, y 24,
3. Condiciones termodinámicas estándares y unidades
Las mezclas de gases–agua–sales por debajo del punto crítico y por encima del punto de congelación del agua pueden presentarse hasta en tres fases en equilibrio: (1) una fase rica en agua líquida, (2) una fase rica en la molécula volátil en estado líquido (distinta de la primera), y (3) una fase de vapor. Así, los estados de referencia y las constantes de equilibrio deben definirse entre todas las fases anteriormente mencionadas. En este trabajo, el estado de referencia para los gases disueltos en la fase líquida acuosa es la solución ideal hipotética disuelta infinitamente a temperatura T, presión total P, y con fracción molar igual a 1. Con este estado de referencia, el coeficiente de actividad de todos los componentes debe acercarse a un valor unitario cuando las fracciones molares sean iguales a cero. Esta estrategia es atribuida al modelo asimétrico de coeficientes de actividad. El cloruro de sodio se considera estar presente solamente en la salmuera en estado líquido y no entra en las otras dos fases.
Para la mezcla de gases y agua en la fase de vapor y la fase rica en la molécula volátil en estado líquido, el estado de referencia es el gas ideal puro a la temperatura del sistema y presión de referencia P0, que convenientemente se tomará a 1 bar. La unidad seleccionada en la fase de vapor es también la fracción molar.
Sabemos bien que el estado de referencia alternativo para la fase líquida acuosa o salmuera conocido en la literatura geoquímica es la solución ideal hipotética a 1 molal (Drum–mond, 1981, Drummond y Ohmoto, 1985; Shock et al., 1989; Johnson et al., 1992). Sin embargo, los dos potenciales químicos de referencia están relacionados entre sí a través de la siguiente ecuación:
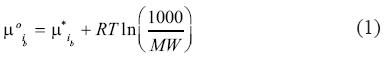
En esta ecuación el exponente * se refiere a la solución ideal hipotética a 1 molal, el exponente 0 se refiere a la solución ideal en dilución infinita con una fracción molar igual a 1 (Wolery, 1990; Anderson y Crerar, 1993). MW se refiere al peso molecular del solvente (en este case, del H2O, que es igual a 18.01528 gramos por mol). El estado estándar adoptado en este trabajo es típico en estudios de equilibrio líquido–vapor en la literatura de ingeniería química y química pura (Kobayashi y Katz, 1953; Danneil et al., 1967; Blount y Price, 1982; Crovetto et al., 1984; Li y Nghiem, 1986; Fernandez–Prini y Crovetto, 1989; Fernandez–Prini, 1992; Søreide y Whitson, 1992; Carroll et al., 1997; Carroll y Mather, 1997; Bakker, 1999, 2003; Fernandez–Prini et al., 2003; Chapoy, 2004), aunque no es muy común en la literatura geoquímica.
4. Modelo termodinámico
4.1 Reacciones, constantes de equilibrio y el potencial químico
En este trabajo explicaremos el equilibrio en términos de potenciales químicos. Por definición, en condiciones de equilibrio, el potencial químico (μ) de cualquier sustancia i (agua, gas o sal) presente en cualquier una fase j (vapor o líquido) debe tener el mismo valor, cumpliéndose así la siguiente ley:
Dentro del rango presión y temperatura de interés geológico podrían potencialmente haber, sin incluir las fases sólidas o supercríticas, más de tres fases diferentes. En las próximas secciones definiremos, por tanto, los tres estados de equilibrio fundamentales de este tratado:
1) el equilibrio entre la fase de gas líquido y la fase de vapor,
2) el equilibrio entre la fase acuosa líquida y la fase de vapor y, por último,
3) el equilibrio entre la fase líquida de una molécula volátil y la fase acuosa líquida.
Adicionalmente, presentaremos constantes de equilibrio K, derivadas de diferencias de potenciales químicos para la cada componente en todas las fases. La fase de gas líquido se denotara con el subscrito l–gas, la fase del vapor por n, y la fase líquida acuosa por l–agua.
4.2 Equilibrio entre los componentes en la fase de gas líquido y la fase de vapor.
El primer componente que estudiaremos será el agua. Consideremos el equilibrio liquido–vapor como una 'reacción' o series de 'reacciones' en donde el H2O que se transfiere está presente y en equilibrio entre la fase de vapor v y la fase de gas líquida de una molécula volátil, tal como esta descrito en la siguiente ecuación:
Similarmente, considérese la reacción de transferencia y el estado de equilibrio del gas i entre la fase de vapor y la fase de gas líquido, descrita por la siguiente reacción
Como el estado de referencia de la fase de vapor es el gas ideal puro a la temperatura del sistema y presión de referencia P0, los potenciales químicos de ambas especies H2O y gas i en la fase de vapor v es igual a:
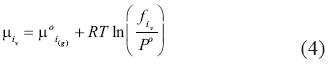
Donde f es la fugacidad, i se refiere tanto al gas como al H2O. Otra vez, μoi(g) es el potencial químico de referencia del gas ideal y R es la constante universal de los gases. Similarmente, para la fase liquida de gas i el valor del potencial químico μ del H2O y del gas i es igual a:
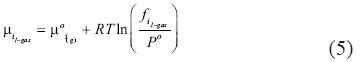
El estado de referencia de los componentes H2O y gas es el mismo en las dos fases (fase liquida del gas y fase de vapor). Por tanto el potencial químico de referencia μoi(g)del gas ideal está presente en las ecuaciones (4) y (5). Por consiguiente, el logaritmo natural de la constante de equilibrio de la reacción está representado por:
La ecuación (6) no es más que la fugacidad del producto sobre la fugacidad del reactante. Sin embargo, K1, también se deriva del principio de igual potencial químico, de manera que:
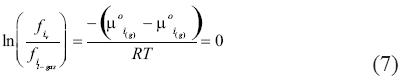
Por lo tanto, K1 es igual a 1. Por esta razón el concepto del equilibrio de fases como una serie de reacciones en las fases de gas no será de mucha utilidad en este estudio. Ahora bien, el caso es diferente para el equilibrio líquido–vapor entre los componentes presentes en la fase vapor y la fase líquida acuosa que puede o no contener sales disueltas, en cuyo caso será llamada 'salmuera' y será descrita con el subíndice b.
4.3 Equilibrio entre la fase de vapor y la fase líquida acuosa o salmuera.
4.3.1 Componente Gaseoso.– Este equilibrio puede ser alcanzado si se considera esta reacción:
Como vimos anteriormente, el potencial químico de gas en la fase vapor n (lado derecho de la reacción anterior) es:
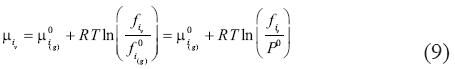
Donde i se refiere al componente gas, el exponente 0 y (g) se refieren al estado del gas ideal a una P de referencia, y f es la fugacidad. R y T mantienen sus significados anteriores. De este modo, la fugacidad del gas en el vapor es:
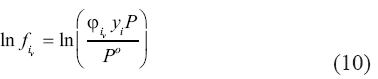
Donde y es la fracción molar del componente i en la fase de vapor n, y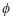 
es el coeficiente de fugacidad en la mezcla, que también depende de y. Re escribiendo las ecuaciones (9) y (10) se obtiene:
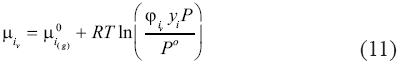
El cálculo de 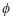iv puede realizarse usando cualquier ecuación de estado, siguiendo procedimientos estándares que serán discutidos más adelante. Ahora que hemos visto como derivar los potenciales químicos de los componentes en las fases, estudiaremos la salmuera. Similarmente, el potencial químico del soluto i en agua, denotado por w es:
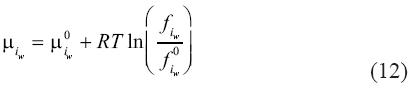
Donde cada símbolo tiene el significado ya definido con anterioridad. Ahora introduciremos dos correcciones al potencial químico. La primera corrección es la dependencia explicita que tiene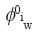 
con respecto a la presión dada por:
Donde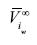 
es el volumen molar parcial del soluto i en agua a dilución infinita. Si la ecuación (13) es integrada desde la presión de saturación Psat y hasta la presión total del sistema P, el potencial químico de referencia sería:
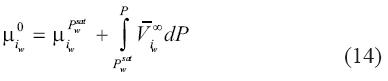
Dejando a la ecuación (12) con la siguiente forma:
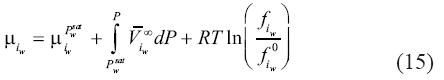
La segunda corrección que se introduce en la ecuación (12) relaciona al potencial químico del soluto en la salmuera μib con el potencial químico del soluto en el agua pura μiw, y es el coeficiente de Setschenov S (Setschenov, 1889). Sabemos por medio de la literatura geoquímica que S ha sido tradicionalmente asociada al coeficiente de actividad a través de la fuerza iónica cuando NaCl es la sal primordial (Anderson y Crerar, 1993). Sin embargo, como se declaró en el documento original S, no es más que una relación empírica (Setschenov, 1889), o una "observación fenomenológica" (Fernandez–Prini, 1992). Debido a su naturaleza, estudios teóricos modernos (Prausnitz et al., 1999) declaran que la diferencia entre el cambio de energía libre de Gibbs de solución de un soluto dentro de un solvente con sal y de un solvente sin sal es:
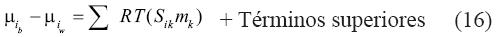
Donde el coeficiente S, es específico para el gas i disuelto en una solución con m moles por kilogramo de sal k. En el presente estudio, seguimos este planteamiento. De esta manera, una expansión truncada de primer orden del potencial químico de la salmuera a presión de saturación sería:
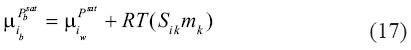
De esta manera, la ecuación (15) se convierte en:
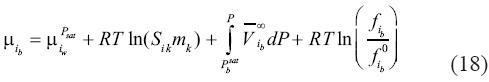
En la ecuación (19) los límites de la integral varían por la presencia de la sal, ya que la presión de saturación de la salmuera varía con el contenido en sal. Por esto hemos sustituido Pwsat por Pbsat , por ,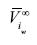 y 
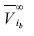f iw por fib. La ventaja de este procedimiento reside en la fexibilidad y capacidad de sustituir la tasa de fugacidades de la ecuación (19) por un modelo de actividad, de manera que:
Finalmente, substituyendo la ecuación (19) dentro de la ecuación (18) resulta:
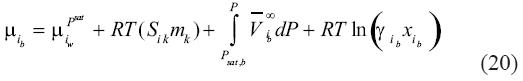
Siguiendo nuestro desarrollo, con el estado de referencia escogido, el coeficiente de actividad γ debe acercase a 1 cuando la fracción molar del soluto (o sal) dentro de la salmuera es cero. Finalmente, igualando (11) con (20) se obtiene:
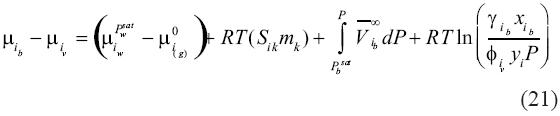
Como el lado izquierdo de la ecuación (21) es cero en equilibrio, se convierte en:
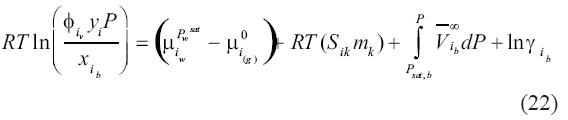
Es necesario expresar la diferencia de potencial químico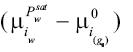 
en el lado derecho de la ecuación (22) en términos de cantidades cuantificables. Esta diferencia puede ser evaluada como:
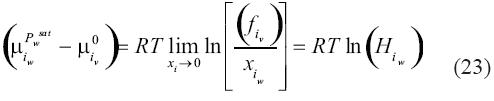
Donde x es la fracción molar del componente i en el agua w, Hiw es la constante de Henry para el gas i en el agua w sin sal, de acuerdo a una de las definiciones típicas. En este experimento teórico, se entiende que la presión alcanza la presión de vapor del agua. La ecuación de equilibrio puede ser finalmente reescrita en una manera conveniente para computación al insertar la constante de Henry. La expresión queda como:
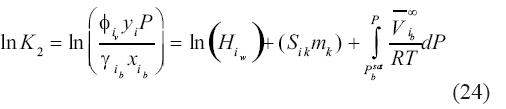
La integración del término de corrección de presión puede hacerse asumiendo que el volumen molar parcial a dilución infinita es independiente de la presión, implicando que la fugacidad del hidrocarburo en la salmuera es:
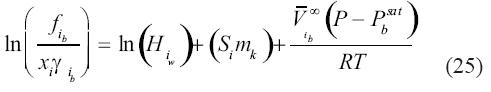
Debe recordarse que la presión de referencia P0 es 1 bar y que, por definición, fi=i,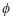iP. El lado derecho de la ecuación (24) constituye la constante de equilibrio K2 para la reacción representada por la ecuación (8) que depende de presión, temperatura y composición.
4.3.2 Componente acuoso.– Ahora consideraremos la reacción representada por la ecuación (26) en donde el agua, presente en la salmuera, de disocia entre la fase líquida acuosa y la fase de vapor:
El potencial químico del agua en la salmuera está dado por:
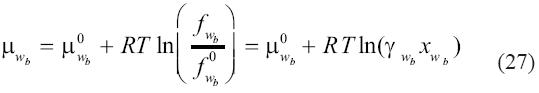
El exponente 0 implica un estado de referencia del agua w en la salmuera b al mezclarse, a temperatura y presión con solutos no volátiles. Con este estado de referencia, la fracción molar xwb se calcula en una base 'libre de sal' y el coeficiente de actividad es igual a 1 cuando esta fracción molar es 1. El potencial químico de referencia puede relacionarse con su valor cuando la presión total es igual a la presión de saturación de la salmuera a una temperatura dada sin gases disueltos. A la presión de saturación, el potencial químico del agua en la salmuera (sin volátiles) es igual al potencial químico del agua en el vapor. Por tanto, sustituyendo:
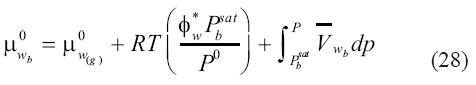
En la ecuación (27) resulta en:
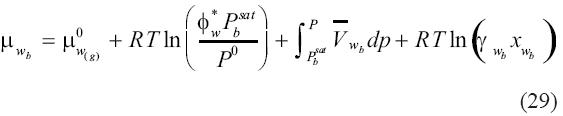
donde μ0w(g) es el potencial químico de referencia del gas ideal a temperatura y presión de referencia P0, Pbsat es la presión de saturación de la salmuera a la temperatura del, Φ*wes el coeficiente de fugacidad de vapor de agua a la temperatura del sistema evaluado al valor de la presión de saturación de la salmuera Pbsat, y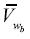 
es el volumen molar parcial del agua en la salmuera. Para enfatizar, la fracción molar en esta expresión es calculada en una base libre de sal y tendrá un valor de 1 cuando no haya solutos volátiles en la salmuera. La integral en la ecuación (29) ha sido evaluada asumiendo un volumen molar parcial del agua en la salmuera independiente de la presión. Por otro lado, el potencial químico del agua en el vapor es:
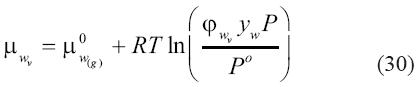
Igualando (29) y (30), reorganizando los términos y resolviendo para la diferencia de potencial químico, se obtiene:
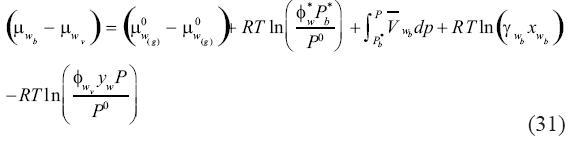
En la ecuación (31) la diferencia (μwb–μwv) y la diferencia (μ0w(g)–μ0w(g))son cero. De este modo, la constante de equilibrio K3, que esta definida como la división de la fugacidad del agua en el vapor entre la fugacidad del agua en la salmuera se expresa como:
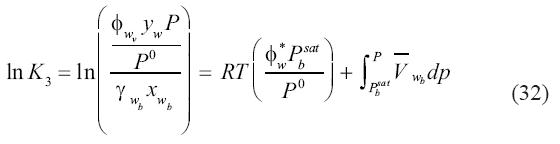
4.4 Equilibrio entre la fase rica en molécula volátil líquida y la fase líquida acuosa o salmuera.
Este equilibrio líquido–líquido puede ser alcanzado al considerar las reacciones representadas por:
Puede que tal equilibrio sólo esté presente en un rango pequeño de presiones y temperaturas. Usando las definiciones empleadas anteriormente, podemos definir el potencial químico de ambos componentes en la fase rica en molécula volátil líquida como:
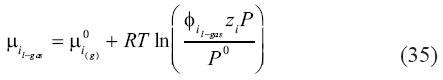
Donde z es la fracción molar de los componentes en la fase rica de molécula volátil líquida l–gas. Nótese que el coeficiente de fugacidad 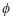ives diferente al coeficiente de fugacidad (es decir, 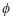iv≠ 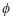iv) usado anteriormente porque son calculados en fases diferentes. Siguiendo el procedimiento descrito anteriormente, las constantes de equilibrio para las reacciones mencionadas son:
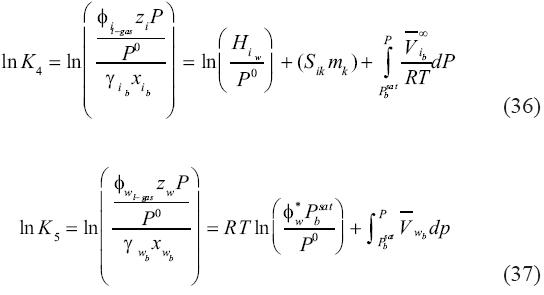
Nótese que las ecuaciones (36) y (37) son equivalentes a las ecuaciones (32) y (24). Las únicas diferencias entre ellas se encuentran en las fracciones molares y los coeficientes de fugacidad, que se calculan para las mezclas en la fase rica de molécula volátil líquida en vez de la fase de vapor.
5. Comparación de este modelo teórico de solubilidad con otros modelos alternativos
Existen varios modelos para estudiar la termodinámica de la solubilidad de gases en salmueras. En esta sección intentaremos realizar una comparación de nuestra teoría con las alternativas existentes en la literatura, y al mismo tiempo compararemos cálculos de solubilidades obtenidos a través del cómputo de nuestras ecuaciones, con cálculos obtenidos a través de los otros modelos.
5.1 Comparación con un modelo de Teoría Escalada de Partícula (SPT).
Esta teoría se basa en la ocurrencia de una cavidad del tamaño de una molécula en una fase líquida. La cavidad se produce debido a fluctuaciones de densidad en el líquido (a nivel molecular) en equilibrio con un gas (Grazziano, 2006). Al aplicar el modelo SPT para estudiar el equilibrio líquido–vapor en un líquido real como el agua con sales disueltas, se considera que el líquido esta compuesto por moléculas esféricas rígidas y se asume que las interacciones atractivas entre las moléculas determinan el volumen ocupado por el líquido, mientras que el tamaño de las moléculas determina las características del ensamblaje (Grazziano, 2006). En este respecto, el trabajo más cercano al nuestro es el de Li y Nghiem (1986) quienes utilizaron una ecuación de estado cúbica para fases no acuosas en equilibrio con salmueras, y SPT para proporcionar una estructura matemática el efecto de las sales disueltas. Los parámetros en este modelo se correlacionan primero con data de solubilidad en agua libre de sal y luego con datos de solubilidades en salmueras. (Li y Nghiem (1986) reportan una alta sensibilidad en los parámetros del modelo.
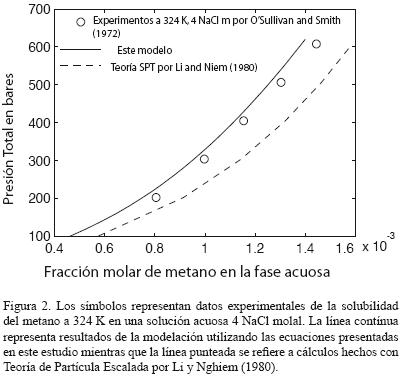
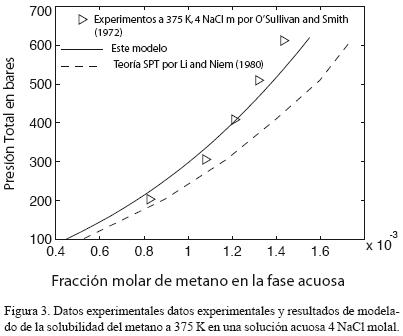
Por otro lado, la definición de la constante de Henry que emplean se basa en su extrapolación a una presión igual a cero bares, en contraste con la presión de vapor del solvente como en el presente trabajo. La complejidad del modelo SPT es alta tanto en su marco teórico como en sus cómputos. Sin embargo, no da resultados más exactos que el modelo propuesto en este articulo. Por ejemplo, veamos la figura 2. En ésta se comparan datos experimentales de solubilidad del metano a diversas temperaturas y molalidades (O'Sullivan y Smith, 1970). Los cálculos que usan los resultados de este estudio se demuestran en línea recta. Por otra parte, la línea discontinua representa los cálculos realizados usando un modelo SPT (Li y Nghiem, 1986). De las dos isotermas calculadas a 4 NaCl m (Figuras 2 y 3) es claro que las desviaciones del modelo SPT son constantemente más elevadas que las desviaciones del modelo presentado. Además, las desviaciones del modelo SPT aumentan con la presión y la concentración del soluto. El error al usar el modelo SPT aumenta desde 3% a 100 bares hasta un 20% a 600 bares, mientras que las desviaciones de los resultados de nuestro modelo no superan el 7% a lo largo de todo el rango de presión.
5.2 Comparación con un Modelo de Interacción Iónica Específica (IIE).
Una segunda alternativa al modelo presentado en este artículo es el modelo de interacción iónica específica (Barta y Bradley, 1985; Duan et al., 1992). En este modelo (IIE), la actividad de los solutos se calcula a partir de una expansión virial de la energía libre de Gibbs en exceso. Los términos cruzados de energía son incluidos para el catión del soluto, el anión del soluto, y las interacciones anión–catión. Los coeficientes se obtienen de manera empírica y deben ser evaluados correlacionándo los datos experimentales. En general, la reproducción de la composición de la fase líquida acuosa es muy buena, con errores inferiores al 3% (Duan et al., 1992). Sin embargo, el "costo" asociado para tener buenas predicciones en la fase acuosa líquida es alto por cuatro razones importantes:
1. Una alta cantidad de constantes deben ajustarse a los datos experimentales. Por ejemplo, el modelo de Barta y de Bradley (1985) para el sistema de CH4–H2O–NaCl ajusta un total de 23 coeficientes. Duan et al. (1992) ajustaron más de 15 parámetros modelados para el mismo sistema.
2. Las regiones líquido–líquido, y las regiones de la fase rica en líquido de molécula volátil no se pueden investigar usando este modelo, porque no se dispone de ecuaciones que lo describan. Adicionalmente, el modelo no produce información sobre el potencial químico del agua en la solución salina.
3. En todos los casos revisados no se consideran las no–idealidades en la fase vapor. Los coeficientes de fugacidad se calculan para los componentes puros y se dejan independientes de la composición.
4. Los errores procedentes de aplicar esta simplificación son pequeños a temperaturas inferiores a 400 K, pero aumentan drásticamente a altas presiones y temperaturas.
Consideramos que la poca exactitud de las predicciones en la fase vapor son la desventaja principal del modelo de Interacción Iónica Especifca. Este punto fue demostrado al comparar datos de la fase líquida rica en molécula volátil con dos resultados obtenidos a través del IIE, uno para el sistema CH4–H2O–NaCl (Barta y Bradley, 1985; Duan et al., 1992) y otro para el sistema C2H6–H2O–NaCl (Mao et al., 2005). Los resultados se ilustran en las Figuras 4 y 5. Según lo mencionado, ambas figuras representan la composición de la fase del vapor del metano–agua y del etano–agua a 477 y 510 K, y presiones totales de 700 bares. Las líneas discontinuas demuestran la consideración de idealidad de la fase vapor usada en el modelo IIE (Duan et al., 1992; Mao et al., 2005).
La línea recta muestra los resultados del modelo desarrollado en el presente trabajo, que calcula todas las no–idealidades. Claramente, en ambos sistemas la consideración de una fase de gas ideal es deficiente, incluso considerando presiones bajas. Semejantemente a las predicciones de Mao et al. (2005), a 300 bares y 510 K, el error en el modelo de Duan et al. (1992) es superior a 10%, mientras que los resultados del presente estudio dan errores menores a 2%.
5.3 Comparación con Ecuaciones de Estado.
También se han desarrollado ecuaciones de estado para el modelado del equilibrio de la fase sal–agua–gas. Estas ecuaciones incluyen la molalidad de la sal como variable dentro del parámetro de interacción binaria para la fase acuosa (Søreide y Whitson, 1992). La molalidad de la sal aparece solamente en el parámetro de interacción, lo cual conduce a inconsistencias termodinámicas. Por ejemplo, el desarrollo de los coeficientes de fugacidad, los balances de masa, y los cálculos del equilibrio ignoran el contenido de sal. A pesar de estas inconsistencias, este método ha sido ámpliamente utilizado, especialmente para reproducir experimentos de solubilidad de hidrocarburos y salmueras. Por ejemplo, se ha ampliado para reproducir la solubilidad del n–butano e i–butano en agua con NaCl (Battistelli et al., 2003). En efecto, este método utiliza dos ecuaciones de estado diferentes para las fases acuosa y no acuosa y no es, en principio, muy diferente del modelo empleado en el presente trabajo. La Figura 6 compara los cálculos de solubilidad a presión baja para el etano y el propano en una solución acuosa de 1 m NaCl.
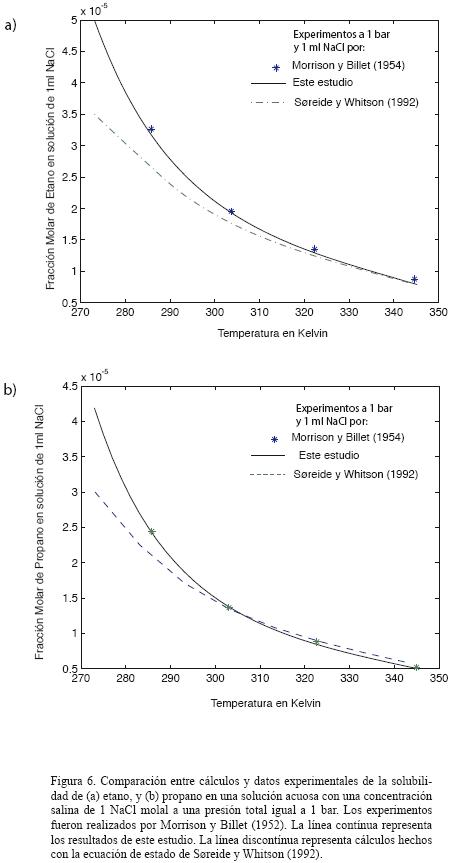
En la figura 6 se aprecia claramente que, a temperaturas inferiores a 345 K, nuestro modelo ofrece resultados óptimos pero a temperaturas mayores ambas simulaciones convergen a una tendencia común y no presentan virtualmente diferencia alguna. En resumen, el modelo que proponemos parece ser más exacto a temperaturas por debajo de 310 K. Más allá de esta temperatura, produce virtualmente los mismos resultados que la ecuación de estado (Søreide y Whitson, 1992). Así, la ventaja de usar el modelo propuesto en el presente trabajo se basa en su consistencia termodinámica con el tratamiento de las sales del soluto y en los cálculos de las características termodinámicas derivadas.
5.4 Comparación con el modelo de Ecuación de Estado extendida BH.
La ecuación de estado de BH se refiere a la ecuación de Bower y Helgeson (1983). En resumen, es otra ecuación de estado cúbica que agrega el efecto de la sal a las reglas de mezclado y se aplica a los sistemas de CO2–H2O–NaCl. A diferencia de los métodos previamente explicados (Søreide y Whitson, 1992) las expresiones de los coeficientes de fugacidad en el modelo BH se derivan de una manera completamente consistente y el NaCl aparece en todas las fases en equilibrio. Este modelo fue extendido para incluir el comportamiento volumétrico en sistemas con CH4 y N2 a temperaturas por encima de la temperatura crítica del agua (Bakker, 1999). Los datos volumétricos a altas presiones y temperaturas en el sistema de CH4–NaCl–H2O están solamente disponibles para el límite del campo de in–miscibilidad (Krader y Frank, 1985) pero la ecuación estado no era capaz de calcular este límite y aparecen desviaciones muy grandes cerca de las condiciones críticas. Las desviaciones pueden llegar a ser hasta 19% en las densidades calculadas para los líquidos ricos en H2O, pero disminuyen y mejoran para los líquidos ricos en CH4 concluyó Bakker (1999), que la ecuación de estado no era conveniente para condiciones de presión y temperaturas altas en el sistema líquido de CH4–NaCl–H2O.
Reprodujimos la extensión de Bakker (1999) del modelo BH y realizamos cálculos de fash bifásico sobre el sistema CH4–NaCl–H2O para temperaturas entre 300 y 600 K, y presiones a 1000 bares. En general, los resultados de nuestro estudio sugieren que la composición de la fase vapor se puede reproducir exactamente con la ecuación BH, con una desviación menor a 14%. Sin embargo, los mismos cálculos sugirieron que la fase líquida en el sistema de CH4–NaCl–H2O no puede ser reproducida. Los resultados en estas predicciones (utilizando el modelo BH en la fase líquida) son un orden de la magnitud más bajos que los valores experimentales, particularmente en las temperaturas inferiores a 500 K. Después de estos cálculos preliminares no se realizaron otras pruebas.
5.5 Comparación con la Ecuación de Estado SPC.
El acrónimo SPC se refiere a la ecuación de estado de Sørensen–Pedersen–Christensen (Sørensen et al., 2002). Este modelo de equilibrio líquido–vapor utilizó la ecuación de estado SRK (Soave, 1972) para las salmueras y para las fases del hidrocarburo, aplicando el llamado 'cambio de volumen' para mejorar la predicción de la presión de vapor (Peneloux et al., 1982) en dicho modelo las sales fueron eficazmente eliminadas de las fases de hidrocarburo durante los cálculos. El modelo utiliza una regla de mezcla de la energía libre de Gibbs basada en un coeficiente de actividad modificado llamado NRTL para las mezclas de sal, del agua y de los gases en la fase líquida acuosa (Huron y Vidal, 1979). Las siglas NRTL (en inglés, "Non–Random–Two–Liquids) pueden traducirse como "Teoría de dos líquidos no azarosos".
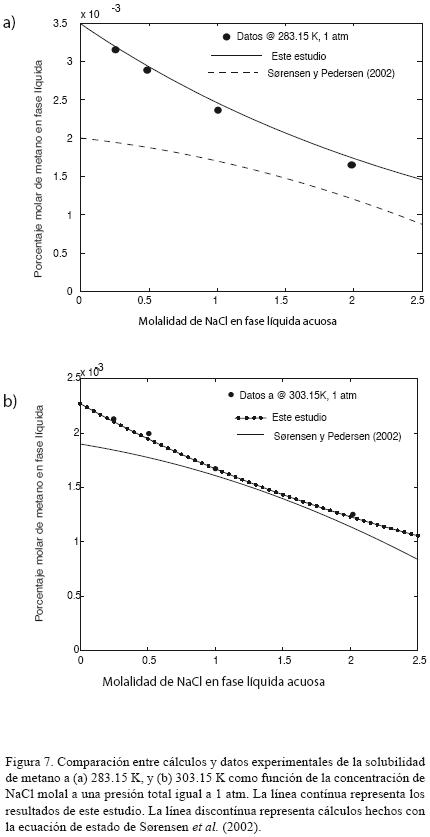
La regla de mezclado utilizando la ecuación SPC permite el uso de hasta tres parámetros por par binario en los datos de correlación de la mezcla. Las reglas de mezclado son incómodas y difíciles de desarrollar y, en general, la exactitud del modelo es baja. La figura 7 compara datos experimentales de la solubilidad a 298.15 y 303.15 K y 1 atmósfera (1.01325 bares) en función de la concentración de NaCl. Los cálculos realizados con el modelo de Sørensen et al. (2002) son representados por una línea discontínua en la figura 7, mientras que los cálculos que usan el modelo presentado en este estudio se ilustran con una línea continua. A partir de la figura 7 queda claro que el uso de reglas de mezclado avanzadas y sofisticadas no conduce a resultados más exactos. La desviación al usar el modelo SPC llega hasta un 11% y aumenta con la concentración de NaCl, mientras que el modelo desarrollado en el presente artículo predice datos experimentales desviándose menos de 2%.
5.6 Otros métodos distantes para modelar mezclas de NaCl–H2O–gases.
La lista de los modelos que predicen solubilidad del gas en soluciones electrolíticas es extensa. Aparte de los modelos ya mencionados, la solubilidad del gas en salmueras se ha modelado usando redes neurales (Schmitz et al., 2006), mecánica estadística y teoría de Monte Carlo (Vorholz et al., 2004), cálculos "ab initio" (Gelb, 2006), e incluso dinámica molecular (Cui y Harris, 1995). Hasta ahora, hemos hecho un esfuerzo considerable en la evaluación de diversos modelos y acercamientos al problema del equilibrio de fases, pero está más allá de alcance de este artículo la comparación de los resultados de este estudio con todos los modelos disponibles en la literatura. Por lo tanto, en las próximas secciones mencionaremos otros modelos relevantes que tratan con equilibrios de fases y salmueras, pero no más allá de la comprensión del método.
Clark y Bishnoi (2004) desarrollaron un modelo mecánico estadístico para realizar los cálculos de equilibrio líquido–vapor. El modelo considera los efectos de cargar los iones, y las interacciones ión–ión de largo alcance. Los parámetros para la solvatacion del ión se agregan a la energía libre de Helmholtz de una mezcla gas–solvente, que es descrita por una ecuación estado cúbica como las perturbaciones a un estado de referencia (Clarke y Bishnoi, 2004). La atención principal del modelo está en la actividad de agua, puesto que el uso principal de la ecuación de estado es modelar el estado de equilibrio de los hidratos. El modelo es útil básicamente para predicciones a altas presiones y bajas temperaturas, y fue diseñado específicamente para la predicción de la estabilidad de los hidratos o clatratos.
Duan y Sun (2003) reportan una ecuación estado para NaCl–H2O–CH4 que amplía una propuesta anterior (Anderko y Pitzer, 1991) para NaCl–H2O. Los efectos del electrolito se incluyen en la energía libre de Helmholtz y en la presión, como perturbaciones a un modelo riguroso para las esferas rígidas. La perturbación se manifiesta como una expansión virial, que introduce un número de parámetros de componentes puros y parámetros binarios de interacción, que deben ser ajustados a datos experimentales (Duan y Sun, 2003). A diferencia de este estudio, el modelo mencionado es bueno para temperaturas netamente superiores a la temperatura crítica del agua.
Zhiping y otros (2005) desarrollaron una ecuación de estado de dos parámetros para las soluciones electrolíticas. El modelo constituye una teoría llamada Aproximación a la Esférica Primitiva Promedio (MSA)" (Prausnitz et al., 1999). La constante dieléctrica en esta teoría (que es dependiente de la concentración) fue intrínsecamente incluida en el modelo, y aspectos de la Teoría Estadística de Asociación de Fluidos (SAFT) fueron introducidos para representar las interacciones de asociación, incluyendo el solvente–solvente y el ión–solvente. Los modelos de MSA y de SAFT contienen un número de parámetros moleculares que se deben ajustar a los datos experimentales (Zhiping et al., 2005). Este modelo se basa básicamente en la teoría mecánica estadística pero no es comparable a este estudio.
6. Propiedades termodinámicas molares estándares
Hasta ahora hemos demostrado que el modelo termodinámico derivado en este trabajo posee una estructura teórica internamente consistente y predice valores de solubilidades con más exactitud que otros modelos encontrados en la literatura. Sin embargo, todavía queda por establecer una relación directa entre las ecuaciones nuestro modelo y valores de referencia de la energía libre de Gibbs parcial molar estándar, así como la entalpía, entropía, y capacidad calórica parcial molar estándar asociada con las reacciones anteriormente descritas. En esta sección demostraremos que derivando parcialmente las constantes de equilibrio encontraremos las propiedades termodinámicas más comunes, de las cuales podrían obtenerse valores internacionalmente aceptados a condiciones ambientales de presión y temperatura. Sólo por claridad hacia el lector repetiremos algunos conceptos anteriormente descritos.
Primeramente, en las mezclas de agua–gas–sal consideramos las siguientes reacciones:
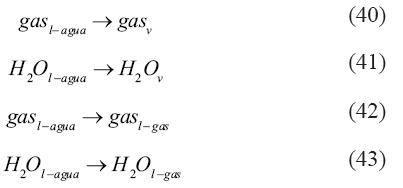
Seguidamente, derivamos las constantes de equilibrio para cada una de las reacciones. La constante de equilibrio para las primeras dos reacciones [ecuaciones (38) y (39)] es igual a 1, ya que arribamos a la solución 1nK1,2= 0. También demostramos que la constante de equilibrio para la tercera y quinta reacción [ecuaciones (40) y (42)] es:
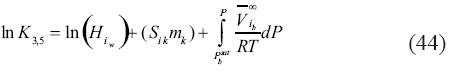
Mientras que la constante de equilibrio para la cuarta y sexta reacción [ecuaciones (41) y (43)] esta representada por:
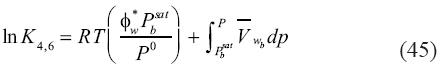
En las ecuaciones (44) y (45) todos los símbolos retienen su significado original. Los subíndices 3 a 6 se referen a la reacción inmediata anterior.
Finalmente, a través de la constante de equilibrio y aplicando relaciones termodinámicas comunes podemos calcular la energía libre de Gibbs parcial molar estándar, definida por:
Mediante simple observación de la ecuación (46) se puede deducir lo siguiente:
1. 
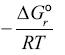para la primera y segunda reacción es igual a cero. Este resultado es consistente porque las substancias son transferidas de una fase a otra, pero dentro del mismo estado de referencia.
2. Para todas las reacciones restantes el valor de 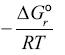se reduce a las constantes de equilibrio mostradas en las ecuaciones (44) y (45).
3. El ΔG°r para la tercera y sexta reacción es función de la presión, temperatura, y contenido de sal.
4. A una presión igual a la presión saturada y con un contenido de sal igual a 0 molal, la ecuación (44) se reduce a la constante de Henry, que sólo es función de la temperatura.
Similarmente, la entalpía, entropía, y capacidad calórica para las reacciones descritas pueden ser calculadas mediante las siguientes relaciones:
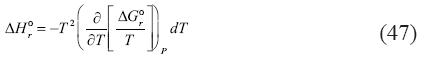
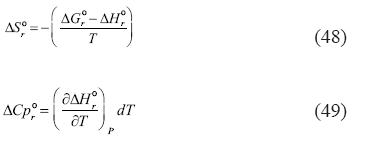
De nuevo, por medio de una simple observación se puede deducir lo siguiente:
5. El valor de ΔH°r, ΔS°r y ΔCp°r para la primera y segunda reacción es cero
6. Los valores de ΔH°r, ΔS°r y ΔCp°r para la tercera y sexta reacción son funciones de presión, temperatura, y salinidad
7. A una presión igual a la presión saturada, temperatura igual 298.15, y una salinidad igual a 0 molal, las ecuaciones de ΔH°r, ΔS°r y ΔCp°r para la tercera y sexta reacción se producirían los valores internacionalmente aceptados, dependiendo de la constante de Henry que se adopte.
7. Conclusiones
En le presente trabajo hemos derivado, por medio de relaciones fundamentales, un modelo termodinámico internamente consistente y útil para describir, reproducir, e interpretar fenómenos cruciales relacionados con la mezcla de gases, agua, y sales disueltas. El modelo acopla la constante de Henry y cualquier ecuación de estado para reproducir datos de solubilidad en las fases líquidas y de vapor. El modelo puede ser utilizado para estudiar tanto sistemas binarios como sistemas de multicomponentes. El modelo es también útil para realizar balances de masas, encontrar propiedades termodinámicas molares estándares relacionadas con las transferencias de moléculas hacia diferentes fases. Basándonos en una revisión extensa de la literatura, concluimos que nuestro modelo esta entre los más simples de programar, y requiere la menor cantidad de parámetros ajustables. Basado en las simulaciones podemos limitar el modelo a temperaturas por debajo del punto crítico del agua, y presiones por debajo de 2000 bares. Este rango de presión y temperatura es suficientemente amplio para aplicar el modelo y entender procesos que ocurren en condiciones geológicas geotermales.
Bibliografía
Anderko, A., Pitzer, K., 1991. Equation–of–state representation of phase equilibria and volumetric properties of the system NaCl–H2O above 573 K: Geochimica et Cosmochimica Acta, 57, 1657–1680.
Anderson, G., Crerar, D., 1993. Thermodynamics in Geochemistry: The Equilibrium Model: New York, Oxford University Press, Inc. , 588 p.
Bakker, R., 1999. Adaption of the Bowers and Helgeson (1983) equation of state to the H2O–CO2–CH4–N2–NaCl system: Chemical Geology, 154, 225–236.
Bakker, R., 2003. Package FLUIDS 1. Computer programs for analysis of fluid inclusion data and for modelling bulk fluid properties: Chemical Geology, 194, 3–23.
Barta, L., Bradley, D., 1985. Extension of the specifc interaction model to include gas solubilities in high temperature brines: Geochimica et Cos–mochimica Acta, 49, 195–203.
Battistelli, A., Oldenburg, C., Moridis, G., Pruess, K., 2003. Modeling gas reservoir processes with TMVOC V.2.0, TOUGH Symposium 2003: Lawrence Berkeley National Laboratory, Berkeley, California, p. 1–8.
Blount, C., Price, L., 1982. Solubility of methane in waters under natural conditions: a laboratory study, Department of Energy Contract Report, DOE/ET/12145–1, p. 159.
Bower, T., Helgeson, H., 1983. Calculation of the thermodynamic and geo–chemical consequences of non–ideal mixing in the system H2O–CO2–NaCl on phase relations in geologic systems; Equation of state for H2O–CO2–NaCl fluids at high pressure and temperatures: Geochimica et Cosmochimica Acta, 47, 1247–1275.
Burrus, R., 2003. Petroleum fluid inclusions, an introduction, in Samson, I., Anderson, A., Marshall, D., editors, Fluid inclusions, analysis and interpretations: Vancouver, Mineralogical Association of Canada, p. 159–169.
Carroll, J., 1992. Use Henry's Law for multicomponent mixtures: Chemical Engineering Progress, 88, 53–58.
Carroll, J., Jou, F., Mather, A., 1997. Fluid phase equilibria in the system n–butane+water: Fluid Phase Equilibria, 140, 157–169.
Carroll, J., Mather, A., 1997. A model for the solubility of light hydrocarbons in water and aqueous solutions of alkanolamines: Chemical Engineering Science, 52, 545–552.
Chapoy, A., 2004. Phase behaviour in water/hydrocarbon mixtures involved in gas production systems, Ph.D. Engineering: Paris, Ecole des Mines de Paris, p. 258.
Chiodini, G., Marini, L., 1998. Hydrothermal gas equilibria: The H2O–H2–CO2–CO–CH4 system: Geochimica et Cosmochimica Acta, 62, 2673–2688.
Clarke, M., Bishnoi, P., 2004. Development of a new equation of state for mixed salt and mixed solvent systems, and applications to vapour–liquid and solid (hydrate)–vapour–liquid equilibria: Fluid Phase Equilibria, 220, 21–35.
Cody, J., Hutcheon, I., 1994. Regional water and gas geochemistry of the Mannville Group and associated horizons, southern Alberta: Bulletin of Canadian Petroleum Geology, 42, 449–464.
Crovetto, R., Fernandez–Prini, R., Japas, M., 1984. The solubility of ethane in water up to 473 K: Ber. Bunsenges. Journal of Physical Chemistry, 88, 484–488.
Cui, S., Harris, J., 1995. Solubility of Sodium Chloride in Supercritical Water: A Molecular Dynamics Study: Journal of Physical Chemistry, 99, 2900–2906.
Danneil, A., Todheide, K., Franck, E., 1967. Verdampfungs gleichtgewichte und kritische Kurven in den Systemen Athan/Wasser und n–Butan/Was–ser bein hohen Drucken: Chemie Ing. Techn., 39, 816–822.
Dohanyosonova, P., Sarraute, S., Dohnal, V., Majer, V., Costa, M., 2004. Aqueous solubility and related thermodynamic functions of nonaromatic hydrocarbons as a function of molecular structure: Industrial and Engineering Chemistry Research, 43, 2805–2815.
Drummond, S., 1981. Boiling and mixing of hydrothermal fuids: chemical effects on mineral precipitation, Geosciences: University Park, The Pennsylvania State University, p. 380.
Drummond, S., Ohmoto, H., 1985. Chemical evolution and mineral deposition of boiling hydrothermal systems: Economic Geology, 80, 126–147.
Duan, Z., Møller, N., Greenberg, J., Weare, J., 1992. The prediction of methane solubility in natural waters to high ionic strength from 0 to 250 degress C, and from 0 to 1600 bars: Geochimica et Cosmochimica Acta, 56, 1451–1460.
Duan, Z., Sun, R., 2003. An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar: Chemical Geology, 193, 257–271.
Fernandez–Prini, R., 1992. Aqueous solutions of nonelectrolytes, in Fernandez–Prini, R., Corti, H., Japas, M., editors, High–temperature aqueous solutions: Thermodynamic properties: Boca Raton, CRC Press, p. 26–72.
Fernandez–Prini, R., Alvarez, J., Harvey, A., 2003. Henry's constants and vapor–liquid distribution constants for gaseous solutes in H2O and D2O at high temperatures: Journal of Physical and Chemical Reference Data, 32, 903–915.
Fernandez–Prini, R., Crovetto, R., 1989. Evaluation of data on solubility of simple apolar gases in light and heavy water at high temperatures: Journal of Physical and Chemical Reference Data, 18, 1231–1243.
Gelb, L., 2006. Ab Initio Monte Carlo Simulations of Fluid Phase Equilibria at Extreme Conditions American Institute of Chemical Engineering, Annual Meeting: San Francisco, AIChE.
Grazziano, G., 2006. Scaled Particle Theory Study of the Length Scale Dependence of Cavity Thermodynamics in Different Liquids: Journal of Physical Chemistry 110 11421 –11426.
Huang, H., Yang, J., Yang, Y. , Du, X., 2004. Geochemistry of natural gases in deep strata of the Songliao Basin, NE China: International Journal of Coal Geology, 58, 231–244.
Hunt, J. M., 1996. Petroleum geochemistry and geology: N Y, W.H. Freeman and Company, 743 p.
Huron, M. J., Vidal, J., 1979. New mixing rules in simple equations of state for representing vapor–liquid equilibria of strongly non–ideal mixtures: Fluid Phase Equilibria, 3, 255–271.
Johnson, J., Oelkers, E., Helgeson, H., 1992. SUPCRT92: A Software package for calculating the standard thermodynamic properties of minerals, gases, and aqueous species and reactions from 1 to 5000 bars and 0 to 1000 C: Computer and Geosciences, 18, 899–947.
Katz, D., Cornell, D., Kobayashi, R., Poettmann, F., Vary, J., Elenbass, J., Weinaug, C., 1959. Handbook of natural gas engineering: New York, McGraw–Hill Book, Inc., 802 p.
Kobayashi, R., Katz, D., 1953. Vapor–liquid equilibria for binary hydrocarbon–water systems: Industrial and Engineering Chemistry, 45, 440–451.
Kotarba, M., Rice, D., 2001. Composition and origin of coalbed gases in the Lower Silesian basin, southwest Poland: Applied Geochemistry, 16, 895–910.
Krader, T., Frank, E., 1985. The ternary system H2O–CH4–NaCl and H2O–CH4–CaCl2 to 800 K and 250 MPa: Ber. Bunsenges. Physical Chemistry, 91, 627–634.
Li, Y., Nghiem, L., 1986. Phase equilibria of oil, gas, and water/brine mixtures from a cubic equation of state and Henry's Law: Canadian Journal of Chemical Engineering, 64, 486–496.
Mao, S., Zhang, Z., Hu, J., Sun, R., Duan, Z., 2005. An accurate model for calculating C2H6 solubility in pure water and aqueous NaCl solutions: Fluid Phase Equilibria, 238, 77–86.
Morrison, T., Billett, F., 1952. The salting–out of non–electrolytes. Part II. The effect of variations in non–electrolyte: Journal of the Chemical Society, 74, 3819–3822.
O'Sullivan, T., Smith, N., 1970. The solubility and partial molal volume of nitrogen and methane in water and aqueous sodium chloride from 50 to 125 C and 100 to 600 atm: Journal of Physical Chemistry, 74, 1460–1466.
Peneloux, A., Rauzy, E., Freze, R., 1982. A consistent correction for Redlich–Kwong–Soave volumes: Fluid Phase Equilibria, 8.
Prausnitz, J., Lichtenthaler, R., Gomez, E., 1999. Molecular Thermodynamics of fuid–phase equilibria: Series in the Physical and Chemical Engineering Sciences: New Jersey, Prentice Hall, 860 p.
Schmitz, J., Zemp, R., Mendes, M., 2006. Modeling and prediction of activity coeffcient ratio of electrolytes in aqueous electrolyte solution containing amino acids using artifcial neural network: Fluid Phase Equilibria, 245, 83–87.
Setschenov, A., 1889. Action de l'acide carbonique sur les solutions des sels a acides forts: Ann. Chim. Phys., 25, 226.
Shock, E., Helgeson, H., Sverjensky, D., 1989. Calculation of the thermodynamic and transport properties of aqueous species at high pressure and temperatures: Standard partial molal properties of inorganic neutral species: Geochimica et Cosmochimica Acta, 53, 2157–2183.
Sloan, D., 1998, Clathrate Hydrates of Natural Gases: Monticello, Marcel Dekker, Inc., 705 p.
Smith, S., Kennedy, B., 1983, The solubility of noble gases in water and in NaCl brine: Geochimica et Cosmochimica Acta, 47, 503–515.
Soave, G., 1972. Equilibrium constants from a modifed Redlich–Kwong equation of state: Chemical Engineering Science, 27, 1197–1203.
Søreide, I., Whitson, C., 1992. Peng–Robinson predictions for hydrocarbons, CO2, N2, and H2S with pure water and NaCl brines: Fluid Phase Equilibria, 77, 217–240.
Sørensen, H., Pedersen, K., Christensen, P., 2002. Modeling gas solubility in brines: Organic Geochemistry, 33, 635–642.
Vorholz, J., Harismiadis, V. , Panagiotopoulos, A., Rumpf, B., Maurer, G., 2004. Molecular simulation of the solubility of carbon dioxide in aqueous solutions of sodium chloride: Fluid Phase Equilibria, 226, 237–250.
Wilhem, E., Battino, R., Wilcock, R., 1977. Low pressure solubility of gases in liquid water: Chemical Reviews, 77, 219–262.
Wolery, T., 1990. On the Thermodynamic Framework of Solutions (With special reference to aqueous electrolyte solutions): American Journal of Science, 290, 296–320.
Yang, S., Cho, S., Lee, H., Lee, C. S., 2001. Measurement and prediction of phase equilibria for water + methane in hydrate forming conditions: Fluid Phase Equilibria, 185, 53–63.
Zhiping, L., Wenchuan, W., Yigui, L., 2005. An equation of state for electrolyte solutions by a combination of low density expansion of non–primitive mean spherical approximation and statistical associating fluid theory: Fluid Phase Equilibria, 227, 147–156.
Manuscrito recibido: Abril 10, 2008.
Manuscrito corregido recibido: Junio 30, 2008.
Manuscrito aceptado: Julio 12, 2008.
