|
BOLETÍN DE LA SOCIEDAD GEOLÓGICA MEXICANA http://dx.doi.org/10.18268/BSGM2008v60n2a4 |
 |
Mechanical instability quantification of slopes at Cofre de Perote volcano, eastern Mexico
Cuantificación de la inestabilidad mecánica en pendientes del volcán Cofre de Perote, México oriental
Rodolfo Díaz Castellón1 ,*, Gerardo Carrasco Núñez2, Alfonso Álvarez–Manilla Aceves1 , 3
1 Posgrado en Ciencias de la Tierra Centro de Geociencias Universidad Nacional Autónoma de México, Campus Juriquilla, Querétaro, Qro. 76230
2 Centro de Geociencias, Universidad Nacional Autónoma de México, Campus Juriquilla, Querétaro, Qro. 76230.
3 Dirección de Estudios de Posgrado de la Facultad de Ingeniería, Universidad Autónoma de Querétaro, Ciudad Universitaria, Cerro de las Campanas s/n, Querétaro, Qro. 76010.
* This email address is being protected from spambots. You need JavaScript enabled to view it..
Abstract
Cofre de Perote (CP) volcano is located at the eastern end of the Trans–Mexican Volcanic Belt (TMVB) at 19°30' Lat N, 97°10' Long W. At a height of 4,282 m.a. s.l, it comprises one of the most massive structures within the Citlaltépetl – Cofre de Perote volcanic range (CCPVR), which constitutes an important physiographic barrier that separates the central altiplano, also known as Serdán Oriental, from the coastal plains of the Gulf of Mexico. This massive structure has repeatedly collapsed, and at least two of the collapse events occurred long after activity ceased, suggesting that even extinct volcanoes may pose an important hazard to nearby populated areas. In the present work, volcanic instability is approached through both quantitative and descriptive methods that include combined numerical analysis of limit equilibrium, calculated with Bishop's modified method, and finite element analysis. The combined techniques were applied after attaining mechanical parameters in the laboratory, the field and through careful geological observations in order to obtain a model that approaches structural conditions prior to the destruction of the volcano.
Reconstruction of the ancient volcano was used to propose an instability model for the modern summit, where maximum stress/ strain relationships before failure were determined for the reconstructed section and actual volcano summit. Results obtained from these models indicate that the volcanic edifice is still unstable, could experience failure in the near future, and should be considered for future hazard assessment.
Key words: volcanic instability, Cofre de Perote, quantitative assessment, inactive volcanoes.
Resumen
El volcán Cofre de Perote (4,282 m.s.n.m); está localizado 19° 30'N; 97° 10' W, 24 km WSWde la Ciudad de Xalapa. Comprende una El volcán Cofre de Perote (4,282 m.s.n.m); está localizado 19° 30'N; 97° 10'W, 24km WSW de la Ciudad de Xalapa. Comprende una de las estructuras más masivas de la cordillera volcánica Citlaltépetl – Cofre de Perote (CCP VR) en el centro–oriente de México: Esta cordillera representa una importante barrera fisiográfica que separa el altiplano central, también denominado como Cuenca del Serdán Oriental, de las planicies costeras del Golfo de México, en el extremo oriental del Cinturón Volcánico Trans–Mexicano (TMVB). Esta estructura ha colapsado repetidamente y, en al menos dos ocasiones, ha sido mucho después del cese de su actividad, sugiriendo que incluso volcanes extintos pueden representar peligros importantes a las poblaciones cercanas. El presente trabajo analiza la inestabilidad volcánica por medio de una combinación de métodos cuantitativos y descriptivos, mediante el método de equilibrio límite a través del modelo modificado de Bishop, y modelación por medio de análisis de elementos finitos. Las técnicas combinadas fueron aplicadas en forma posterior a la obtención de parámetros mecánicos en el laboratorio y en el campo, en combinación con cuidadosas observaciones geológicas que dieron como resultado un modelo que aproxima las condiciones de estabilidad estructural previa a la destrucción del volcán. Estas observaciones fueron utilizadas para recrear la destrucción de la cima con el objeto de determinar las condiciones de estabilidad actual, y en donde ambas técnicas combinadas ayudan a determinar las condiciones de esfuerzo–deformación previas a la falla. Los resultados obtenidos de esta modelación indican que el edificio volcánico continúa siendo inestable y que un evento recurrente debe ser considerado en la evaluación de peligros.
Palabras clave: Inestabilidad volcánica, Cofre de Perote, evaluación cuantitativa, volcanes inactivos.
1. Introduction
Quantifiable determination of mechanical instability conditions was until just a few years ago a field exclusive to civil engineering and other disciplines associated with construction and infrastructure works (i.e. Duncan, 1996; Yu et al., 1998). Studies of the mechanical characteristics of large sectors of single volcanoes have been performed only very recently and are, for the most part, mainly descriptive and/or combined with structural geology measurements (i.e. Tibaldi et al., 2003), which might be because of the increased need in computer power required for slope stability quantification. However, advances in computer technology along with continued breakthroughs in the understanding of rock mass behavior have helped simulate complex scenarios with a high degree of certainty at a low cost. Studies of mechanical instability of a complex scenario like that found on a volcano slope imply considerations regarding the hydraulic conductivity, coupled interface between contiguous strata, and combined joint behavior of the volcanic massif.
Furthermore, most of the works dealing with volcano slope instability focus on the destruction of edifices linked to the presence of a magmatic component (i.e. Siebert et al., 1987), leaving the structural behavior of inactive or dormant volcanoes practically unexplored. There are several weakening factors that have to be considered when attempting an evaluation of the structural integrity of volcanoes such as: emplacement features, alteration conditions (either by past hydrothermal activity or weathering), tectonic stress, fracturing, discontinuities other than fracturing (i.e. stratification, dikes, breccias, pyroclastic deposits), and water pressure, amongst the most important. Some external triggering factors have to be considered also, for example, excessive rainfall and/or earthquakes. Although there are additional factors associated with volcanic instability, for instance those related to volcanic activity, they are not mentioned here because this paper is focused on factors affecting inactive or extinct volcanoes.
Cofre de Perote (4,282 m.a.s.l.) is an extinct volcano that has repeatedly collapsed long after its activity ceased (Carrasco–Núñez et al., 2006). It constitutes the northern end of the Citlaltépetl–Cofre de Perote Volcanic Range (CCPVR) at the eastern part of the Trans–Mexican Volcanic Belt (TMVB) (Figure 1).
The instability conditions for Cofre de Perote (CP) volcano have been attained by consideration of the factors described above in order to determine whether there are enough destabilizing elements to account for a renewed collapse, or if the volcano has become stable enough to be considered as a "safe" structure. This approach considers data extrapolated from overlapping failure models using limit equilibrium analysis, with stress/strain relationships obtained from finite element modeling. By combining these techniques, complemented by careful observations and aided by a reconstruction of ancestral collapses, we have obtained enough information to determine the maximum allowed deformation and stress required to induce failure.
2. Geologic evolution of Cofre de Perote volcano
From a morphological perspective, CP volcano can be defined as a compound shield volcano, as it has low–grade slopes and does not have a single eruptive conduit, but rather the volcanic materials were extruded through several eruptive centers in a dome–like manner (Figure 2). Amongst CP's main morphological features are its soft slopes, which provide a deceptive perception that the volcanic edifice is stable.
The evolution of CP can be divided into three marked and distinctive construction stages and at least two confirmed destruction periods (Carrasco–Núñez et al., in preparation). The first stage of construction was dated by K/Ar at about 1.3±0.1 Ma (Carrasco–Núñez and Nelson, 1998) and corresponds to basaltic andesites located at the SE flank of Cofre de Perote. Some older lavas have been reported nearby, such as those collected east of Perote and dated at 1.7 and 1.9 Ma (Yañez–García and García–Durán, 1982), as well as one lava sample collected east of Xalapa and dated by Cantagrel and Robin (1979) at 1.57±0.05 Ma (Pleistocene); nevertheless, the relation of these older lavas to the CP volcanic activity is not certain. This first stage of construction is characterized by intense effusive activity from multiple eruptive centers, which resulted in a large volcanic field that comprises the basal part of CP volcano. These observations could explain the difference in age, given the volcano is not comprised of a single structure, but in reality constitutes an entire volcanic field. The oldest lavas at CP volcano are mostly composed of olivine and augite basaltic andesite and do not present a strong contrast in composition (Carrasco–Núñez and Nelson, 1998). The dominant rocks belonging to the first stage of construction are porphyritic and occasionally show a seriated texture. The mineralogy of these rocks comprises mainly plagioclase and augite crystals within a matrix that includes microlites of plagioclase and pyroxenes. Some samples display alteration minerals, particularly iron oxides (hematite and/or magnetite) and skeletal and sieve textures are visible in some plagioclase crystals. The mineralogy is similar in most samples belonging to this stage, with plagioclase and augite phenocrysts surrounded by a glassy re–crystallized matrix being the most characteristic features.
After a long period of quiescence, for which no record of volcanic activity is present, the second stage of construction started about 0.4 My ago (Carrasco–Núñez et al., in preparation); it is characterized entirely by effusive activity, as reported for earlier lavas. At this stage, lavas are clearly ooverlie deposits of the Xaltipán ignimbrite, dated at 0.46±0.02 Ma (Ferriz and Mahood, 1984). Effusion rates for this period were apparently continuous until the cease of activity (Carrasco–Núñez and Nelson, 1998). Samples belonging to the second stage show a seriated porphyritic texture, similar to the rocks of the first stage. The rocks are mainly composed of plagioclase phenocrysts and two pyroxenes (hyperstene and augite). The matrix for these samples is coarse–grained and is mostly constituted by microlites of plagioclase, altered olivine crystals and magnetite, although glass is also present in a few samples.
The last stage of construction is constituted by rocks dated at 0.24±0.05 Ma (Carrasco–Núñez and Nelson, 1998). These rocks vary in composition from intermediate to felsic and display characteristic porphyritic textures with plagioclase phenocry sts in a microlithic matrix with pyroxenes, magnetite and, in a few cases, recrystallized glass. In contrast with lavas corresponding to the first and second stages, skeletal textures are not present in the lavas of the last stage.
We have found no evidence of explosive activity for any of the construction stages of the volcano and, given its dimensions, it is not likely that the structure ever showed such behavior. However, evidence shows that lavas belonging to second stage of construction are overlying pyroclastic deposits belonging to Los Humeros caldera, particularly toward its western flank. These deposits correspond to the Xaltipán ignimbrite (Ferriz and Mahood, 1984).
The last evolutionary stage of CP volcano is marked by two periods of destruction that generated massive collapses at about 42 K and 10 K years ago (Carrasco–Núñez et al., 2006). These events produced widespread volcanoclastic deposits towards the east long after the cease of CP activity (0.24±0.05 My). Those deposits are known as Los Pescados Debris Flow and Xico Avalanche, respectively (Carrasco–Núñez et al., 2006).
3. Structural parameters affecting the instability of Cofre de Perote volcano
Stability conditions described below are similar to those involved in any rock mass structural quantification (i.e. Cai et al., 2007; van Wyk de Vries and Borgia, 1996); however, the regional tectonic setting and local volcanic stratigraphical conditions must be considered for an appropriate stability assessment.
For a comprehensive stability assessment of a volcanic edifice, regardless of its size, a detailed description of the factors affecting its structural integrity is required. In most cases, volcanic instability is only evaluated from a general and/or descriptive point of view (i.e. Carrasco–Núñez et al., 2006; López and Williams, 1993); however, sometimes a more quantitative methodology is used (i.e. Concha–Dimas et al., 2005). The quantitative approach presented here considers modeling that can be used either as a single methodology or in combination with other methods for assessing the structural conditions of volcanic structures and other types of rock masses.
The first step in a structural evaluation should be to obtain the mechanical parameters that will be used in the model. Detailed geology and knowledge of representative structural features are fundamental for assessing structural properties, fracturing being the most significant factor given its importance to rock mass structural behavior.
In addition, hydrothermal alteration has been proposed as a major weakening factor by several authors (Watters and Delahaut, 1995; López and Williams, 1993); therefore, the intensity and distribution of alteration has to be assessed when determining structural integrity. The role of alteration is very important in restricting the rock mechanical response at altered areas nearby or next to brecciated deposits, usually underlying massive and unaltered lava flows.
4. Fractures
Major structural features represented on the geologic map (Figure 2) are most likely related to tectonic aspects. They were identified from digital aerial ortorectified images (scale 1:20,000, pixel size 2 meters) in order to delineate major fractures and alignments (Figure 3). Rose diagrams reveal a NE–SW preferential orientation, which is parallel to the structural alignment followed by three volcanoes comprised by Cerro Desconocido, Cofre de Perote and Las Lajas. According to Lagmay et al. (2000) and Nakamura (1977), this alignment might indicate the principal horizontal stress (σ2), where (σl) would correspond to the gravitational load of the structure over the supporting surface.
Rose diagrams of fractures were elaborated following two different criteria: by fracture density (Figure 3a) and by fracture length (Figure 3b). We identified at least three major fracture patterns: NW–SE, N–S, and NE–SW. If tensile forces determine fracture orientation, slip surfaces should follow a direction normal to the mean fracture orientation, indicating the most likely direction of failure in a sector is oriented parallel to the tensile horizontal stress (normal to main scarps). Furthermore, results from direct field measurements represented by pole diagrams indicate a similar stress orientation mainly NW–SE and N–S (Figure 4).
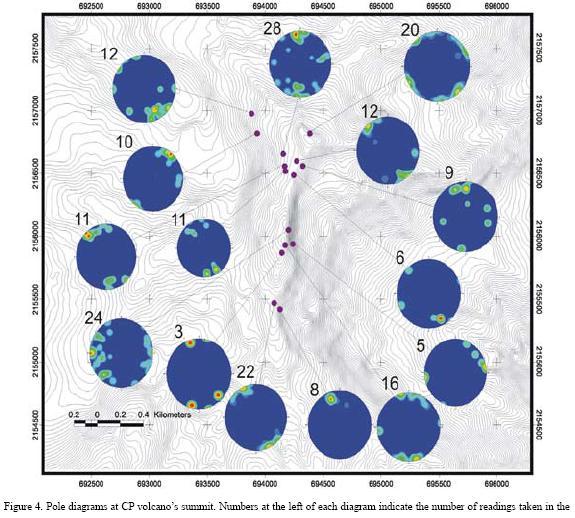
5. Basement control
Carrasco–Núñez et al. (2006) proposed that along the CCPVR the sloping substrate was one of the most important factors controlling the collapse of all major volcanic structures towards the east. This is supported also by observing the folding orientation of the basement structures (Concha–Dimas et al., 2005), and the interpretation of the rose diagrams of faults generated over the supporting tilted limestones (Mossman and Viniegra, 1976), which have facilitated collapses towards the east. In any case, under these conditions fractures are expected to be normal to the direction of tilting (Merle and Borgia, 1996), rendering the basement as the controlling mechanism for induced structural instability and failure direction of the collapsed volcanoes.
6. Mechanical characterization of Cofre de Perote volcano
So far, only structural parameters such as fractures and orientations have been considered, however, in order to evaluate local slope instability, two fundamental aspects need to be considered: discontinuities and rock properties. Discontinuities are comprised of joints, stratification, foliation, faults and fractures, and all are considered as planes of weakness (Watters et al., 2000). Chemical alteration of rocks is another important factor to be considered, as intact rock strength varies according to the intensity of alteration, where intensely altered rocks have a very low strength. Also, alteration in discontinuities such as joint filling has to be considered when describing the rock mass (Bieniawski, 1989).
Determination of rock structural properties is difficult because rock fabric differs from most studied materials and the rock properties are far from behaving in an "ideal" form, being anisotropic, heterogeneous and discontinuous. Although rock mass strength varies in some cases up to several orders of magnitude from that of the intact rock, rock strength represents the upper limit of strength for any given rock mass (Bieniawski, 1989).
Mechanical behavior of fresh rocks without secondary fractures can be considered as elastic materials that experience fragile failure, rendering very high elastic moduli and a limited ability for deformation. In contrast, rock masses are dependant on rock strength and behave more as plastic materials. They are affected by the number and distribution of discontinuities and allow stronger deformation with continual stress/strength redistribution as slopes deform. We extracted core probes from selected samples collected at the Cofre de Perote summit in order to determine intact rock strength. Selection of these rocks was done according to visual variations in chemical alteration conditions, varying from apparently fresh to strongly altered rocks. Samples were tested under axial load (Figure 5) following ASTM (American Society for Testing Materials) compliances (ASTM Standard D7012, 2007). Different rock mechanical responses were observed under axial load, whereas one of the samples presented relatively higher resistance, showing an abrupt failure (Figure 5a) and suggesting fragile failure, another sample failed more rapidly presenting a series of fractures with different orientations (Figure 5b).

Mechanical response and vertical deformation of rocks from several locations at the CP summit were measured by using a Schmidt hammer, and strain/stress diagrams were drawn to determine the type of failure, and rock strength (Table 1).
The main parameters obtained through mechanical testing were strain/strength relations, elastic modulus (E), maximum stress allowance (σ) and deformation (ε) (Table 1).
Strength results suggest that an external factor such as hydrothermal alteration might be responsible for the low resistance obtained in the laboratory and in the field (Diaz Castellón, under revision)
Because wave propagation is ruled by density and Lamé parameters, some sites were selected for geomechanical profile characterization using the Vp/Vs (compression and shear velocity) ratio (Álvarez–Manilla et al., 2003). Travel time of "S" and "P" waves determines elastic characteristics of the media, and corresponds to shear and compressive waves. These signals are compared with the distance from the acoustic source and registered against the arrival time.
Seismic waves propagate throughout a discontinuous media according to Hook's Law, and are transmitted in two forms: dilatation or compression (also known as "P" waves); and transversal or shear (also known as "S" waves). The Poisson Ratio, Rigidity, Young, and Bulk Dynamics Deformation Modulus were determined by using the propagation velocity and bulk density relationship. A final parameter derived from seismic survey by the ratio " Vp/Vs" was the internal friction angle, under elastic deformation according to Álvarez–Manilla et al. (2003).
7. GSI Geological Strength Index
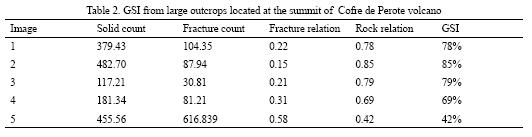
The Geological Strength Index (GSI) is one of the most widely used methods to characterize the structural features of any given rock mass, using descriptive conditions of the rock mass (i.e. Bieniawski, 1973). Despite the fact that the parameter is highly effective, Cai et al. (2004) have proposed a method to assess the GSI in a semi–quantitative way, considering several quantifiable parameters to achieve a highly acceptable and more adequate index.
In this paper, we approach the problem by using digital image analysis. To estimate the rockmass area, an initial calibration of the pixel size is required, and after a pre– processing treatment involving the enhancement of structural features, the image is separated into rock and fractures, and finally an estimative value of the GSI is obtained.
However, the method cannot consider some factors such as fracture condition and alteration; therefore, a detailed description of the fractures including filling material, water, type of joints and alteration is necessary for pixel calibration. These considerations are introduced into the kernel used to calibrate the image, in order to obtain a more accurate GSI (Figure 6). Using the traditional method for GSI, where alteration or fracture conditions are not considered, a value of 0.866 was obtained, which differs from our estimate of 0.78 (Table 2). The main difference between both techniques is that our method considers the rockwall while traditional measurement considers only a one–dimension analysis. Consequently, it is expected that GSI values in digital evaluation are more conservative than traditional methods; nevertheless, it should be more accurate.
8. Limit equilibrium analysis
In order to determine the mechanical conditions of the volcano, a reconstruction of its summit was carried out based on present topographical conditions, and estimated volume of the volcaniclastic deposits from past collapse events. For that purpose, the paleotopography was obtained (Figure 8) by interpolating the missing elevation contours and softening the scarp configuration (Figure 7) to a slope similar to that of the eastern lower flanks.
The limit equilibrium analysis approaches a problem through lineal comparison of active Vs resisting forces. All acting forces (af) (negative) and resisting forces (rf) (positive) are added, and equilibrium is considered to be present if the result is positive or "zero", and "zero" is considered as limit equilibrium. Another approach named the "safety factor (SF)"consists of dividing both sets of forces (rf/af), "one" being the lowest value for equilibrium. This is the most widely used method in numerical modeling for most engineering projects, including the present work
Using more precise data makes it possible to get closer to a "safety factor" of one, in contrast, a safety factor of two or even larger might not mean anything if the input data is corrupt or statistically poor.
The limit equilibrium analysis performed in this paper follows the Hoek et al., (2002) criterion and uses the commercial software named "Slide" (Rocscience, 2003), where failure surfaces are estimated according to constitutive equation proposed by Mohr–Coulomb, where shear strength is controlled by the relation τ = c + σtan(φ), and where: τ = shear strength; c = cohesive strength; σ = uniaxial compressive strength; φ = internal friction.
This condition suggests a lineal behavior of a slip surface which according to Hoek et al., (2002) might yield unrealistic safet safety parameters and lead to underestimate stability conditions at any given slope.
To compensate for such underestimations, Hoek et al., (2002) proposed a model to estimate mechanical properties of rock masses since 1980, which has evolved up until today and it is expressed in the form:
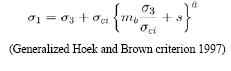
Where: σ1 σ3 = major and minimal principal strengths; σci. = uniaxial compressive strength; mb, s, a = Hoek and Brown constants.
Constants "s" and "m" depend on a physical alteration parameter designated as disturbance (D) (Hoek et al., 2002); this parameter influences both constants and for the present evaluation, it has been interpreted as loss of confinement because of a missing part of the structure. In other words, tilting of the basement or basement deformation due to emplacement of the volcanic edifice, along with loss of confinement from the missing summit, help increase the disturbance factor "relaxing" its summit and favoring unstable conditions of the volcanic edifice.
9. Limit equilibrium analysis on a reconstructed CP
Regardless of the triggering factors that caused the volcano to collapse, relaxation due to the retirement of confinement from missing parts of the summit, irregular basement support, rock weakness due to hydrothermal alteration (Díaz–Castellón et al., 2004) and strong fracturing are amongst the most important structural parameters controlling instability of the volcano. Results from a seismic exploration survey suggest that relaxation of the summit is possible. In a test conducted normal to the main scarps, acoustic wave travel velocities were reported to be slower than those observed parallel to the main scarps, suggesting that a stronger fracture pattern is present in that direction with tension fractures formed in the same direction.
Relaxation of the summit suggests that a high disturbance factor (D = 0.7) (Hoek et al., 2002) should be used in the numerical evaluation. A comparison of the actual topographical cross section, derived from an elevation model using 1:50,000 scale digital topographical data from INEGI (1984, 1987a, 1987b, 1990) (E14B26, E14B27, E14B36, E14B37) with a modified section showing the inferred paleotopography is shown in Figure 8. The geological cross sections were obtained from available data (Figure 2). Although the model is simple, it comprises the main structural parameters identified in the field and from laboratory tests. Because the model considers the constitutive equation proposed by Mohr Coulomb, and the model approaches the problem through the constitutive equations of Hoek et al. (2002), the authors suggest here an empirical model to adjust from the generalized Hoek and Brown (1997) criteria to the Mohr Coulomb model.
The first reconstructed model considers normal gravitational forces because of the presence of the volcanic massif. Under normal conditions the modeling shows multiple failure surfaces, which do not reach instability conditions. The selected surface for numerical evaluation was done by taking the largest slip surface closest to limit equilibrium (Figure 8), that is, the largest surface area, which was closest to 1 in the most critical scenario. For our approach we selected Bishop's modified method and a model comprised of 20 slices or sections.
Seismic acceleration and an increased neutral pressure induced by a hydrostatic water column can be proposed as the main triggering factors, however, because of the rock mass characteristics and height of the waterhead, it becomes clear that hydrostatic pressure might not create unstable conditions. Nevertheless, several calculations varying the height of the waterhead indicated that excess hydrostatic pressure is not likely to destabilize the structure. Liquefaction as a seismically induced process provoked by a reduced resistance to shear strength (Colindres–Selva, 1993) can also be a factor to be considered; however, results indicate that this is not a likely scenario because the principal requirements, hydrostatic pressure and a granular media, are not present at CP. Furthermore, numerical verification confirmed that water does not represent a destabilizing element in this particular case.
To determine instability conditions of the reconstructed volcano modeled under stable conditions, a constant horizontal pull of 0.1 g was applied in an attempt to simulate seismic acceleration. In order to have consistent results, we proposed the same failure surface used to assess structural conditions in the reconstruction of the static model (Figure 8).
Although we lack acceleration information for the CCPVR area and 0.1g might seem arbitrary, there are records of a historic 6.5 Richter magnitude earthquake named the Xalapa earthquake of 1920 (Flores and Camacho, 1922; Suárez, 1992), that factor alone suggests this type of acceleration could be achieved. For that reason, and based on an acceleration model prepared for the western United States (Mualchin, 1996), we found that a relatively low 5.2 Richter magnitude earthquake at a maximum distance of 15 km could be enough to accelerate the ground and reach the proposed 0.1g.
Our results suggest that if such acceleration is reached it would result in a force strong enough to destabilize the volcano from an "SF" of 1.053 to 0.798. However, we recognize that further analysis will be needed to verify those considerations.
10. Finite element analysis
In contrast with limit equilibrium, our determinations using finite element analysis approaches the problem considering rock mass strength rather than rock strength to determine strain/stress relationships. These parameters, strong earthquake would be enough to destabilize the structure and induce failure of its summit. derived from rigidity and bulk modulus ("G" and "K"), are determined directly in the field aided by seismic refraction exploration methods.
The modulus mentioned above along with the other parameters (Table 3) are drawn directly from the relationship of the propagation velocities between dilation or compression waves (VP) and the transversal or shearing waves (VS) (Álvarez–Manilla et al., 2003) where:
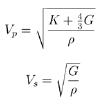
Mechanical results were applied to the reconstructed sec¬tions used on limit equilibrium analysis at CP; where strain/stress was plotted considering shear conditions. Actual methodology considers total stress energy deformation.
To follow the same criteria, we used again a horizontal pull of 0.1g caused from a seismic dynamic load, and a vertical gravitational acceleration of 1g.
The deformation field (Λ(e)) is assessed through the expression of energy where a deformation continuum can be proposed for each finite element by means of the expression:
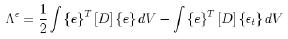
Where: {εt} = Thermal deformation field; [D] = Elastic constants matrix, {e}= Total deformation.
To produce an accurate mesh of the section, it is necessary to use finite elements with second degree shape constants because the section is complex, especially when attempting to mesh finite elements that are larger that the minimum separation between distances comprising the section. In the case of a finite element of four sides, which is the type used for the present model, each element has eight shape constants with two degrees of freedom on each node of the finite element (X, Y).
The main input parameters used to evaluate strain/stress conditions were: gravitational acceleration, maximum horizontal pull of 0. 1g, elastic modulus, and Poisson relationship of slopes retrieved from seismic exploration (Table 3). Since the model used to evaluate stability is a 2D section, the mechanical model approaches a solution through planar deformation, therefore, it is necessary to suggest a thickness for each section, which in this case is unitary (1 m).
Constitutive equations applied to each finite element allow to evaluate creep, strain, stress and hardening.
For most of the sections, finite element meshing was at a separation of 50 m between each finite element where massive layers of lava and basement rocks are present. For other materials such as pyroclastic and/or breccia deposits, a finer mesh was elaborated, considering a separation between continuous elements of 20 m.
Results of the reconstruction of CP volcano's summit considering a 0. 1g acceleration gave us an estimated shear stress distribution for the section. After overlapping the results from limit equilibrium analysis on the shear stress model, it is possible to obtain an estimation of shear stress at the time of failure (Figure 9). A second model of shear strain was elaborated to determine the maximum deformation allowed at the time of failure. Estimation results suggest the maximum strain allowance at the time reaches critical conditions (Figure 10).
11. Evaluation of the present structural conditions at CP volcano
In order to assess the present structural conditions at CP volcano we used the same methodology applied to the reconstruction of the volcano; however, in this case and in order to increase accuracy, six sections were produced, which are perpendicular to the scarps and consistent with fracturing conditions.
The first results from the six sections evaluated show large failure surfaces, which are slightly above an SF of 1 or very close to it (Figure 11). After a horizontal pull of 0. 1g was applied (Table 4) it becomes clear that a relatively.
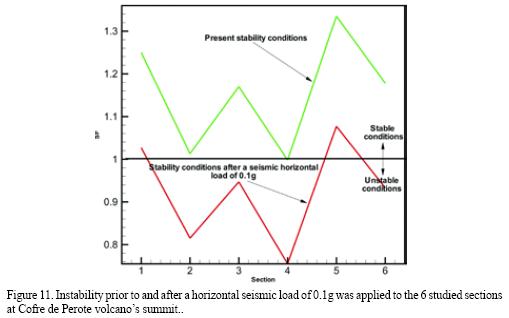
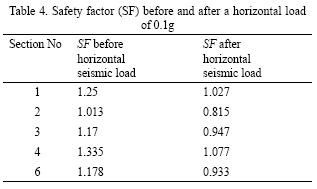
Evaluation of all sections, considering both methods, shows that an estimated 700–1,000 KPa shear strength might be enough to trigger collapse. Graphics for all sections were elaborated considering average areas and depths, where an estimated 0.5 km3 of material (Figure 12) is prone to collapse if a strong earthquake takes place near CP.
12. Discussion
The methodologies discussed here have been derived from techniques and models widely used in engineering projects, although they are usually applied separately. Here, different techniques are combined to determine strain/stress relations on the volcanic massif. Additional methods such as digital image processing helped to determine the mechanical parameters of rock masses in an innovative way of determining the GSI, which must be used along with the Hoek and Brown constitutive equations for the determination of the Hoek and Brown (1997) constants. Moreover, evaluation of instability conditions at Cofre de Perote volcano must be considered an important issue for civil protection, especially because large populated areas are located on top of deposits from previous collapses of CP. This is the first approach to consider geotechnical instability conditions of the volcano's summit.
Structural parameters of the CP volcano are strongly associated to its geologic evolution and are affected by external mechanical processes, which are more characteristic of the structure itself. Nevertheless, many of its structural features that are visible today are clearly inherited from the regional volcanic tectonic settings.
From the reconstruction of CP volcano, it is clear that instability conditions in the past were similar to those that are present today, and that reconstruction of past events renders close results to those observed today at its summit. These observations also confirm that our structural considerations are adequate.
Although our estimations show that even an earthquake similar to the Xalapa earthquake of 1920 could trigger a sector collapse, there is still uncertainty as to what happened at CP summit during this event. All reports indicate that it triggered landslides of several slopes along the Huitzilapan River, which generated a massive debris flow (Flores and Camacho, 1922), however, there is no record of collapses at CP. This might be related to civil protection issues, since the 1920 debris flow completely devastated a community called Barranca Grande (Scott et al., 2001); consequently, little or no attention was given to other areas. On the other hand, we should also consider that propagation of the seismic waves did not impact the CP in a direct way, and may be associated to structural conditions between the epicenter and the CP summit.
13. Conclusions
From a volcanological perspective, analysis of instability at CP provides important implications for hazard assessment of extinct volcanoes that are believed to represent relatively safe conditions to nearby populated areas. The results of this study may imply that volcanic structures with a similar setting and evolution might also be unstable, representing a hazard to populated areas located near the path of their main drainage systems and along structurally unstable zones.
We conclude that sector collapse without the presence of a magmatic component is possible, as has been demonstrated in the past by multiple slope failure of the CP summit area (Carrasco–Núñez et al., 2006), which occurred long after it became extinct. Furthermore, our work provides enough information to show that a weakened volcano can experience sector collapse aided by discrete external triggers such as earthquakes, and favored by extreme climatic conditions even though they did not represent a triggering factor here. Reconstruction of sector collapse shows a strong similarity between proposed scenarios and present topography at CP's summit, suggesting conditions prior to ancient collapses were similar to those present at the actual volcano summit
Finally, it has been determined that a strong 6+ earthquake in an area near CP volcano could trigger massive landslides and their most probable path would be towards populated areas along Los Pescados River
Acknowledgments.
We would like to specially thank CONACYT for grant 44549–F, which financed this project. Dr. Paul Garnica provided useful comments and facilities by the use of the laboratories at the Instituto Mexicano del Transporte (IMT), and Dr. Jaime Horta (Universidad Autónoma de Querétaro, U AQ) and Dr. Lucía Capra made valuable comments on the text. Ms. C. Sara Solís Valdez helped us to edit most of the figures, and José Luis Rodriguez Vargas helped us during the fieldwork. Finally, we would like to thank the Centro de Geociencias, under the direction of Dr. Luca Ferrari, and personnel for their continued support and Sergio Rodríguez and an anonymous reviewer for their final comments on this paper.
References
Álvarez–Manilla Aceves, A., Garnica–Anguas, P., Pérez Salazar, A., 2003, Evaluación indirecta de los módulos elásticos de rigidez in situ y la relación entre Vp/Vs y el ángulo de fricción interna: Sanfandila, Querétaro, Instituto Mexicano del Transporte, Publicación Técnica 225, 39 p.
American Society for Testing Materials, ASTM Standard D7012, 2007, Standard test method for compressive strength and elastic moduli of intact rock core specimens under varying states of stress and temperatures, ASTM International, West Conshohocken, PA.
Bieniawski, Z.T., 1973, Engineering classification of jointed rock masses: Transactions of the South African Institution of Civil Engineers 15, 335–344.
Bieniawski, Z.T., 1989, Engineering rock mass classifications: a complete manual for engineers and geologists in mining, civil and petroleum engineering: New York, John Wiley and Sons, 251 p.
Cai, M., Kaiser, P. K., Uno, H., Tasaka, Y., Minami, M., 2004, Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system: International Journal of Rock Mechanics and Mining Sciences, 41, 3–19.
Cai, M., Kaiser, P. K., Tasaka, Y., Minami, M., 2007, Determination of residual strength parameters of jointed rock masses using the GSI system: International Journal of Rock Mechanics and Mining Science, 44, 247–265.
Cantagrel, J. M., Robin, C., 1979, K–Ar dating on eastern Mexican volcanic rocks – relations between the andesitic and alkaline provinces: Journal of Volcanology and Geothermal Research, 5, 99–114.
Carrasco–Núñez, G., Nelson, S., 1998, Edad y tasa de crecimiento del volcán Cofre de Perote (resumen), Primera Reunión Nacional de Ciencias de la Tierra: México D. F., 41.
Carrasco–Núñez, G., Díaz–Castellón, G., R., Siebert, L., Hubbard, B. E., Sheridan, M. F., Rodríguez–Elizarrarás, S. R., 2006, Multiple edifice–collapse events in the Eastern Mexican Volcanic Belt: the role of sloping substrate and implications for hazard assessment: Journal of Volcanology and Geothermal Research, 158, 151–176.
Carrasco–Núñez, G., Siebert, L., Díaz–Castellón, R., Vázquez–Selem, L., Evolution and edifice stability conditions of a compound shield–like volcano: Cofre de Perote, Eastern Mexican Volcanic Belt (in preparation).
Colindres–Selva, S. R., 1993, Dinámica de suelos y estructuras, 2nd ed.: México D.F., Limusa, 648 p.
Concha–Dimas, A., Cerca, M., Rodríguez, S. R., Watters, R. J., 2005, Geomorphological evidence of the influence of pre–volcanic basement structure on emplacement and deformation of volcanic edifices at the Cofre de Perote–Pico de Orizaba chain and implications for avalanche generation: Geomorphology, 72, 19–39.
Díaz Castellón, R., Hubbard, B., Carrasco–Núñez G., Sheridan, M. F., 2004, Hydrothermal alteration and debris flow/avalanche hazards at Cofre de Perote (México), in IV Reunión Nacional de Ciencias de la Tierra: Juriquilla, Querétaro, Mexico. 145–146.
Díaz–Castellón, R., under revisión, Análisis de la estabilidad estructural del volcán Cofre de Perote: Mexico, Universidad Nacional Autónoma de México, Ph. D. thesis.
Duncan, J. M., 1996, State of the art: Limit equilibrium and finite–element analysis of slopes: Journal of Geotechnical Engineering, 122, 7, 577–596.
Ferriz, H., Mahood, G. A., 1984, Eruption rates and compositional trends at Los Humeros Volcanic Center, Puebla, Mexico: Journal of Geophysical Research, 89, 8511–8524.
Flores, T., Camacho, H., 1922, Memoria relativa al terremoto mexicano del 3 de enero de 1920: Boletín del Instituto Geológico de México, 38, 107 p.
Hoek, E., Brown, E. T., 1997, Practical estimates of rock mass strength: International Journal of Rock Mechanics and Mining Sciences, 34, 1165–1186.
Hoek, E., Carranza–Torres, C., Corkum, B., 2002, Hoek–Brown failure criterion – 2002 edition: Proceedings 5th North American Rock Mechanics Society Symposium and 17th Tunneling Association of Canada, Toronto, Canada, 1, 267–273.
Instituto Nacional de Estadística Geografía e Informática, (INEGI), 1984, Carta topográfica Coatepec E14–B37, 1:50,000 scale: México, D. F., Secretaría de Programación y Presupuesto, Instituto Nacional de Estadística, Geografía e Informática, 1 map.
Instituto Nacional de Estadística Geografía e Informática, (INEGI), 1987a, Carta topográfica Perote E14–B26, 1:50,000 scale: México, D. F, Secretaría de Programación y Presupuesto, Instituto Nacional de Estadística, Geografía e Informática, 1 map.
Instituto Nacional de Estadística Geografía e Informática, (INEGI), 1987b, Carta topográfica Xalapa E14–B27, 1:50,000 scale: México, D. F, Secretaría de Programación y Presupuesto, Instituto Nacional de Estadística, Geografía e Informática, 1 map.
Instituto Nacional de Estadística Geografía e Informática, (INEGI), 1990, Carta topográfica Xico E14–B36, 1:50,000 scale: México, D. F, Secretaría de Programación y Presupuesto, Instituto Nacional de Estadística, Geografía e Informática, 1 map.
Lagmay, A. M. F., van Wyk de Vries, B., Kerle, N., 2000, Volcano instability induced by strike–slip faulting: Bulletin of Volcanology, 62, 331–346.
López, D. L., Williams, S. N., 1993, Catastrophic volcanic collapse: relation to hydrothermal processes: Science, 260, 1794–1796.
Merle, O., Borgia, A., 1996, Scaled experiments of volcano spreading: Journal of Geophysical Research, 101, 13805 – 13817.
Mossman, R. W., Viniegra, F., 1976, Complex fault structures in Veracruz Province of Mexico: American Association of Petroleum Geologists Bulletin, 60, 379–388.
Mualchin, L., 1996, A technical report to accompany the Caltrans California seismic hazard map 1996 (based on maximum credible earthquakes): Sacramento, California, Department of Transportation, 65 p.
Nakamura, K., 1977, Volcanoes as possible indicators of tectonic stress orientation – Principle and proposal: Journal of Volcanology and Geothermal Research, 2, 1–16.
Rocscience Inc. 2003, Slide Version 5.0–2D Limit equilibrium slope stability analysis: Toronto, Ontario, Canada, http://www.rocscience.com.
Scott, K. M., Macías, J. L., Naranjo, J. A., Rodriguez, S., McGeehin, J. P., 2001, Catastrophic debris flows transformed from landslides in volcanic and tropical terrains: mobility, hazard assessment, and mitigation strategies: U.S. Geological Survey Professional Paper 1630, 59 p.
Siebert, L., Glicken, H., Ui, T., 1987, Volcanic hazards from Bezymianny–and Bandai–type eruptions: Bulletin of Volcanology, 49, 435–459.
Suarez, G., 1992. El sismo de Jalapa del 3 de enero de 1920: Revista Mexicana de Ingeniería Sismica, 42, 3–15.
Tibaldi, A., Corazzato, C., Apuani, T., Cancelli, A., 2002, Deformation at Stromboli volcano (Italy) revealed by rock mechanics and structural geology: Tectonophysics, 361, 187–204.
van Wyk de Vries, B., Borgia, A., 1996, The role of basement in volcano deformation, in McGuire, W. J., Jones, A. P., Neuberg, J. (eds.) Volcano instability on the Earth and other planets: Geological Society, London, Special Publications, 110, 95–110.
Watters, R. J., Delahaut, W. D., 1995, The effect of argillic alteration on rock mass stability: Geological Society of America Reviews in Engineering Geology, X, 139–150.
Watters, R. J., Zimbelman, D. R., Bowman, S. D., Crowley, J. K., 2000, Rock mass strength assessment and significance to edifice stability, Mount Rainier and Mount Hood, Cascade Range volcanoes: Pure and Applied Geophysics, 157, 957–976.
Yañez García, C., García Durán, S., 1982, Exploración de la región geotérmica de Los Humeros–Las Derrumbadas, estados de Puebla y Veracruz: México D. F., Comisión Federal de Electricidad, Technical report, 96 p.
Yu, H. S., Salgado, R., Sloan, S. W., Kim, J. M., 1998, Limit analysis versus limit equilibrium for slope stability: Journal of Geotechnical and Geoenvironmental Engineering, 124, 1, 1–11.
Manuscript received: February 6, 2008
Corrected manuscript received: June 15, 2008
Manuspcrit accepted: June 26, 2008

