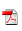|
BOLETÍN DE LA SOCIEDAD GEOLÓGICA MEXICANA http://dx.doi.org/10.18268/BSGM2008v60n1a5 |
 |
Evolution of the geometry of normal faults in the Oligocene volcanic field of the Mesa Central, Mexico
Evolución de la geometría de fallas normales en el campo volcánico del Oligoceno en la Mesa Central, México
Xu Shunshan1,*, Ángel F. Nieto–Samaniego1, Susana A. Alaniz–Álvarez1 and José Manuel Grajales–Nishimura2
1 Universidad Nacional Autónoma de México, Centro de Geociencias, Apartado Postal 1–742, Querétaro, Qro., 76001, México.
2 Instituto Mexicano del Petróleo, Eje Central Lázaro Cárdenas No. 152, Col. San Bartolo Atepehuácan, C.P 07730, México, D.F., México.
*This email address is being protected from spambots. You need JavaScript enabled to view it.
Abstract
We document that the direction of fault traces and the long axis of volcanic domes show a similar distribution, which indicates that the normal faults controlled in some way the location of volcanic rocks. In this study we analyze the evolution of the faults from a geometric point of view, without considerations about the volcanic processes. Bed tilt was controlled by fault block rotation with continuous fault activity. Multi–peak profiles of bed tilt along the fault strike and evident corrugation of the fault traces in the study area should be partly due to segment linkage during fault evolution. Some normal faults are associated with mode I fracture mechanism, whereas some other faults are due to mode II fracture mechanism according to the calculated initial dips. The plot of maximum fault displacement (D) versus trace length (L) is very scattered. Faults with D/L ratios larger than 0.l and smaller than 0.1 can be distinguished; these two fault groups are produced by the effects of fault evolution and sampling. The principal factor influencing D/L ratios is the interaction and linkage among the faults. In addition, fault block rotation, fault initial mechanism, lithology of volcanic rocks, and denudation are other factors.
Key words: Normal fault, bed tilt, fault growth, Mesa Central, Mexico.
Resumen
Se documenta que la dirección de las trazas de las fallas y de los ejes mayores de los domos volcánicos muestran una distribución similar, lo cual sugiere que las fallas normales controlaron de alguna manera la localización de las rocas volcánicas. En este trabajo se presenta un estudio sobre la evolución geométrica de las fallas sin considerar el fenómeno volcánico. El estudio muestra que la inclinación de las capas fue controlada por la rotación del bloque de la falla con actividad continua. Además, se observó que los perfiles de inclinación de capas a lo largo del rumbo de las fallas contienen multipicos, y que sus trazas son corrugadas, esto puede ser debido a la unión de segmentos de falla durante su evolución. Algunas fallas normales se asocian al mecanismo de fractura modo I, mientras que otras están asociadas al mecanismo de fractura modo II, considerando las inclinaciones iniciales calculadas de las fallas. Se estudió además la relación entre el desplazamiento máximo (D) y la longitud de la traza de la falla (L). El diagrama entre (D) y (L) es disperso pero las fallas con las razones D/L > 0.1 y < 0.1 pueden ser diferenciados. Estos dos grupos de fallas se interpretan como productos de los efectos de la evolución y del muestreo del fallamiento. El factor principal que influye en la razón D/L es la interacción y el acoplamiento (linkage) entre segmentos de fallas. Además, la rotación del bloque de la falla, el mecanismo inicial, el tipo de roca y el efecto de la denudación son otros factores posibles.
Palabras claves: falla normal, basculamiento de capa, crecimiento de fallas, modo del crecimiento, Mesa Central, México.
1. Introduction
Volcanic vent alignments commonly appear within volcanic fields and have been interpreted as indicators of the local stress field (Alaniz–Álvarez et al, 1999, 2002a). The alignments are perpendicular to the minimum principal compressive stress, and then must be parallel to traces of normal faults. If the displacement on faults and emplacement of volcanic rocks are coeval, it is expected that rollover pattern is formed in the hanging–wall (Childs et al, 2003). These structures can be observed in the field.
In general, the orientation of crustal shear produced by faulting is unknown and depends on the orientation, location and number of individual faults. The amount of horizontal stretching calculated from faults depends on what shear orientation was assumed (White et al, 1986). Additional complications are introduced by the amount of horizontal strain accommodated by ductile deformation of beds, and from the volume occupied by magmas.
The shape of fault displacement profiles may depend on the material properties, the boundary conditions and the growth mechanism (e.g. Cowie and Scholz, 1992a, 1992b; Cowie et al., 1993). The displacement distribution is also strongly affected by fault linkage, showing significant differences if it is soft–link (e.g. Walsh and Watterson, 1991) or hard–link (Childs et al., 1995; Fossen and Hesthammer, 1997). A normal fault intersecting the free surface generally shows a complicated evolution. Walsh and Watterson (1987) proposed that syn–sedimentary faults have different growth curves in comparison with non–syn–sedimentary faults. The physical experiment carried out by Mansfield and Cartwright (2001) has shown that the faults which intersect the free surface have very irregular displacement profiles after linking.
In the southern Mesa Central, in central Mexico, a large number of normal faults developed in the Oligocene volcanic rocks. Faulting occurred in multiple phases with ages from the Oligocene, coeval with volcanic rocks emplacement, to Miocene, postdating the volcanism (Aranda–Gómez et al., 2007; Nieto–Samaniego et al. 1999). The purpose of this work is to use that region as a case of study to: (1) analyze if the normal faults determined the location of volcanic vents; (2) analyze the relationships between maximum displacements and trace length of faults and (3) determine key parameters of the fault geometry evolution.
2. Geological setting
The study area is within an elevated plateau in central Mexico located in the south of the Mesa Central (Figure 1). The elevation of southern Mesa Central is higher than 2000 m. a.s.l. and the crust thickness in this region is about 32 km (Nieto–Samaniego et al., 2005). The outcrops of the oldest rocks in the southern Mesa Central are Triassic marine rocks, which are overlain by marine Mesozoic strata. Most part of the study region is covered by continental Cenozoic sedimentary and volcanic rocks. There is an angular unconformity between the Mesozoic and Cenozoic sequences. The bottom of the Cenozoic sequence consists of conglomerate, andesite and rhyolite of Paleocene–Eocene age. Oligocene rocks consist of topaz–bearing rhyolites and ignimbrites forming an extensive cover with a peak of volcanism at 30 Ma and minor activity at 27–25 Ma. The uppermost part of the Cenozoic sequence is Pliocene–Pleistocene alkaline basalt (Nieto–Samaniego et al, 2005).
There are three major normal fault systems in the study area (Figure 1). The first one is El Bajío fault system which is located in the southern boundary of the Mesa Central. This fault set consists of two segments. The eastern segment trends near East–West and has a minimum throw of 350 m. The second segment shows a NW–SE strike, forms the SW edge of the Sierra de Guanajuato having in that zone a maximum displacement of 1200 m. The peak activity of El Bajío Fault was between the Oligocene and the middle Miocene (Quintero–Legorreta, 1992, Nieto–Samaniego et al., 2005). The second major fault system is the ~N–S trending Taxco–San Miguel de Allende fault system. This fault system bounds the Mesa Central to the East and was active during the Oligocene and Miocene, with a throw of 450 m, measured in San Miguel de Allende (Alaniz–Álvarez et al, 2002b). The third major fault system is the San Luis–Tepehuanes fault that trends NW–SE crossing the Mesa Central. This fault system was active during Eocene to Quaternary and is still active in Durango region (Barajas–Gea, 2008). There are many smaller normal faults in the study area that forms a rhombohedral pattern in map view (Barajas–Gea, 2008; (Nieto–Samaniego et al, 2005).
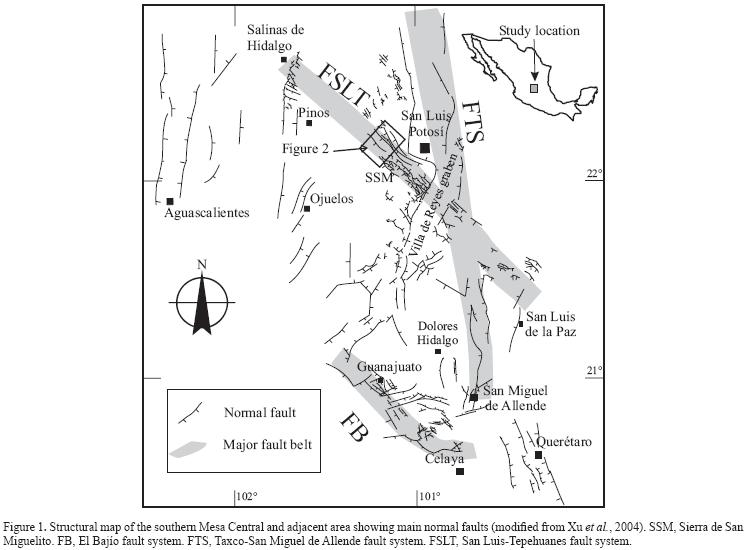
We selected the Sierra de San Miguelito as a detailed study area (Figure 2). The fault system in San Miguelito has been regarded as having a "domino style" because it consists of sub–parallel faults that systematically tilt the volcanic beds to the NE (Labarthe–Hernández and Jiménez–López, 1992; Xu et al, 2004). On the whole individual faults have a strike direction of N20°W– S60°E and dips to the SW. The striations on the fault surfaces are observed to plunge SW (occasionally SE) with a pitch of 75°–85°. There are some faults with N or NE strike direction. Their main activity was dated by Nieto–Samaniego et al. (1999) between 30.0 and 26.8 Ma, coeval with the emission of the Cantera Ignimbrite and ended with the emplacement of the upper Panalillo Rhyolite (Labarthe–Hernández and Jiménez–López, 1992).
3. Relationship between faulting and bed tilt and distribution of volcanic domes
In this section, first, we will study the change of tilts along a sampling line perpendicular to the faults and the distribution of volcanic domes. In domino–style faulting the normal faults progressively diminish dips as the extension proceeds. As the faults rotate the stratigraphic units are also tilted. There are three main explanations for the fault tilting. One is based on the rigid body rotation model, which assumes that faults bound rigid blocks, the tilt angles of beds and faults are equal to each other and there is no internal deformation within fault blocks. The second one is based on the vertical shear model proposed by Westaway and Kusznir (1993). This model considers that the internal deformation within a block bounded by faults is due to vertical shear. The third is the oblique shear model (White et al, 1986), which proposes that the internal deformation within blocks is due to arbitrary oblique shear. For the two latter cases the tilt of beds near the faults is larger than that far from the faults. In the case of the Sierra de San Miguelito, the tilting of the Panalillo Rhyolite has been studied by Xu et al. (2004). The results indicate the tilting of beds in the Sierra de San Miguelito is due to vertical shear or inclined shear.
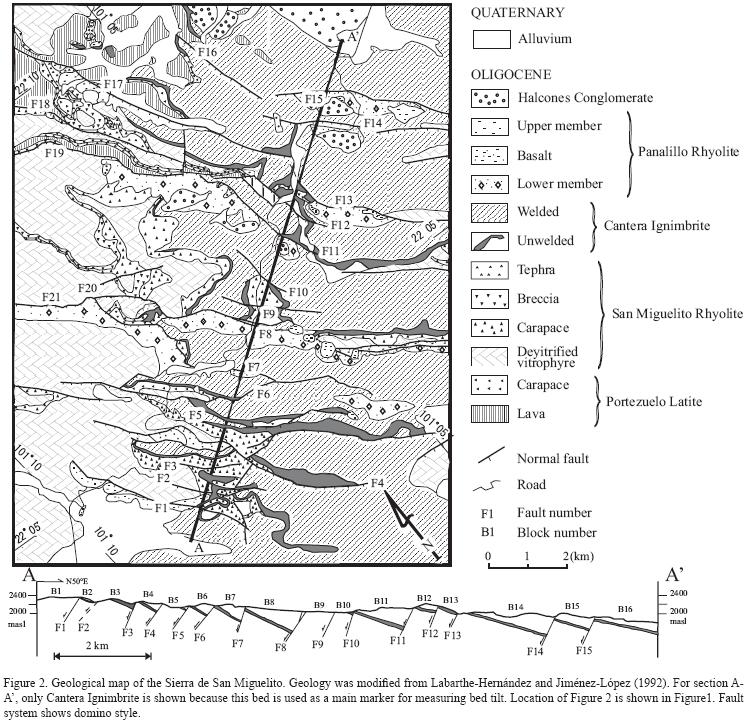
An exercise in order to test that the normal faults control the location of volcanic vents, was collecting the data of volcanic domes from the maps of the southern Mesa Central published at 1:50,000 and 1:20,000 scales (e. g. Labarthe–Hernández et al, 1982; Labarthe–Hernández and Jiménez–López, 1992, 1993, 1994). The distribution of volcanic domes is shown in Figure 3. A rose diagram of the larger axis of volcanic domes shows two preferred orientations (Figure 4a): N30°–50°W. Those directions are the same obtained from strikes of main faults in the studied area (Figure 4b). The coincidence of fault strikes and orientation of the long axis of volcanic domes and dome alignments, suggests that magma might migrate through the pre–existing fault zones, and then reached the surface.
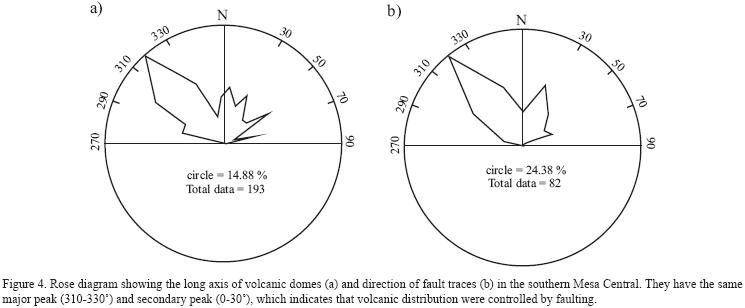
4. Formation of the normal faults
We observed abundant columnar joints in the study area (Xu et al., 2004). These joints are sub–vertical. They should be normal faults if their dips become small due to rotation of rock body and initiate displacement. The aim of this section is to study mechanism of faulting by restoring the initial dips of faults and joints that rotated during faulting.
It has been documented that the tilt mechanism of normal faults in San Miguelito is near vertical shear (Xu et al, 2004, 2005). Considering the vertical shear model of Westaway and Kusznir (1993), bed tilt (θ), present fault dip (δ), and the original fault dip (δi) are related by
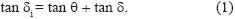
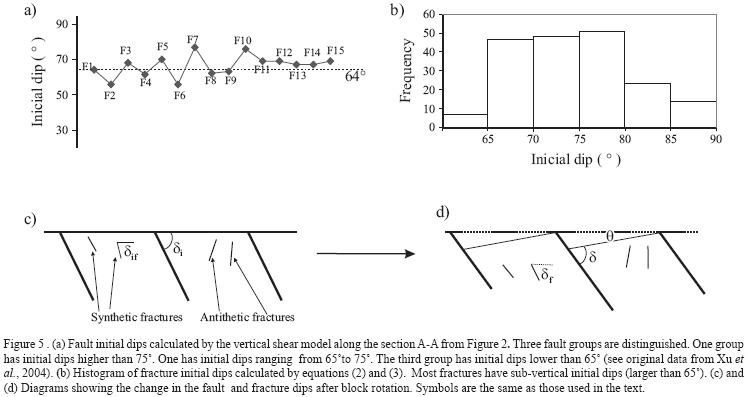
The initial fault dips calculated by Eq. 1 along the section A–A' in Figure 2 are showed in Figure 5a. It can be seen that six faults (faults 1, 2, 4, 6, 8, 9) have initial dips smaller than 65° that is the expected initial dips estimated by Xu et al. (2004) under Andersonian principle of conjugate shears. These six faults formed under the mode II fracture mechanism (Figure 6a, b). Two faults (faults 7 and 10) have initial dips larger than 75°. These two faults can be considered as due to the mode I fracture mechanism. The initial dips of other faults range from 65° to 75°. For these faults, there are two possible explanations. First, these faults are formed when direction of σi was not vertical, but had an angle of 10–15° with vertical plane. Second, these faults can be interpreted as inherited faults. Wilkins etal. (2001) named this type of faults faulted joint at outcrop scale. These faults initiated as opening–model fractures (joints) with 90° of dip, the joints were subjected to shear traction due to the misalignment of the principal stress. The rock block, where joints are located, can rotate rigidly within an unchanged regional stress field. The rotation may be due to the activity of larger faults where fractures are located nearby. When these joints have dips from 65° to 75°, the joints began to slip and become faults (Sneddon and Lowengrub, 1969; Wilkins et al., 2001) (Figure 6c, 6d). Therefore, their initial dips calculated by equation (1) are not true initial dips, but apparent initial dips. Their true initial dips are larger than 75°.
The initial dips of fractures (δif) that are synthetic to the fault and are located within a fault block can be calculated by the equation

where δif is initial dip of fracture, δf is measured dip of fracture.
For antithetic fractures, their initial dips can be calculated by the following equation

These two equations are only for the fractures that formed at the same time as major block–bending faults. If the fractures formed after the fault, the calculated values of initial dip will be less than the real initial dips. The deviations cannot be estimated because detailed relative ages of fractures are unknown. We estimated the initial values (δif) for 192 fractures synthetic with the faults of the SSM (Figure 5b), most fractures have initial dips larger than 65°, which indicates that they formed under the mode I fracture mechanism shown in Figure 6c, d. Some small faults may be derived from these original fractures as inherited faults or faulted joints according to Wilkins et al.. (2001).
The fractures with initial dip larger than 75° are columnar joints (Xu et al., 2004). The columnar joint strikes are parallel to those of the normal faults for mode I. If the synthetic joints in a fault block rotated due to larger fault or due to change on the regional stress field, the joint dips decrease. On the other hand, if the antithetic joints in a fault block rotated due to larger fault or due to change on the regional stress field, the joint dips increase. When the joint dips reach 90°, the values will decrease again (Figure 5c, 5d). When the joint dips become smaller, the shear stress on the joints will increase. As a result, the displacement initiates on joints and became inhered faults. Our results indicate that the columnar joints whose strikes are parallel or sub–parallel to those of the normal faults in the study area played an important role in forming normal faults. These inhered faults from joints will become larger with repeated displacement and could accommodate part of the total strain (Xu et al., 2004).
5. Bed tilt profiles and fault dip along fault strike
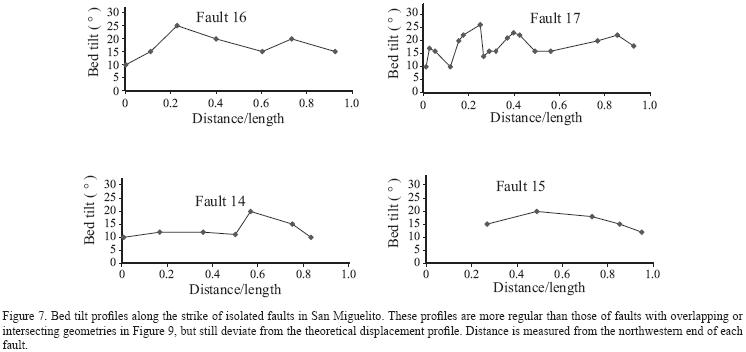
Bed tilt and fault dip along fault strike provide important information about fault linkage, fault formation, and lithologic influence on faulting process. The bed tilt in our study area is due to continuous fault slip along dip direction (Xu et al., 2004). As a result, the larger bed tilt represents a larger fault slip (Westaway andKusznir, 1993). This feature is also documented in bed tilts of synsedimentary faults (Childs et al., 2003). Therefore, the bed tilt profiles will be similar to the displacement profiles, if the faults are assumed to form after volcanism. The data of bed tilt were obtained from the Oligocene Cantera Ignimbrite, not only because they have well developed measurement markers, but also because they formed at the period of strong fault activity. The points measured are close to the fault plane to our best ability. This is important since the bed tilts vary considerably across a fault block due to the vertical shear or oblique shear (Xu et al., 2004). Values from one to ten measurements data for each point are used to construct the bed tilt profiles. The error estimated is 2–3°, which may represent a relative error of 10–15%. The results are shown in Figures 7 and 8, where the horizontal coordinate is normalized distance (distance/length).
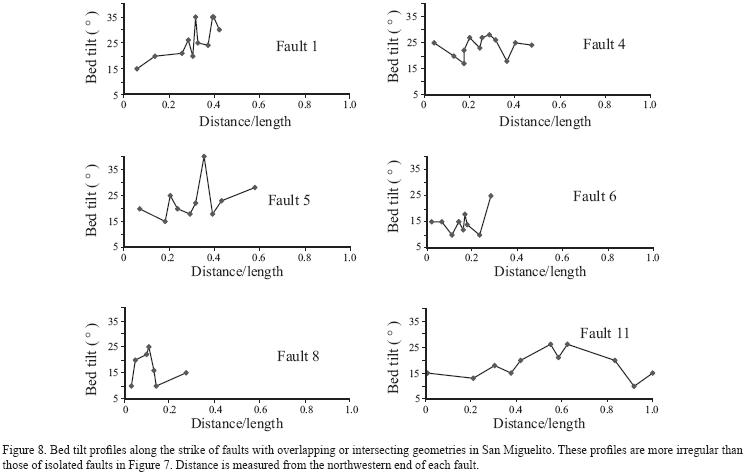
The characteristics of the bed tilt profiles show very irregular and multipeak curves for the faults that are intersected or overlapped by other faults. The isolated faults show more regular profiles, but they are not consistent with other published isolated faults (e.g. Dawers et al, 1993; Dawers and Anders, 1995; Fossen and Hestammer, 1997). Multipeak curves suggest that the faults in the study area experienced complicated evolution and fault linkage (e.g. Segall and Pollard, 1983; Gudmundsson, 1987; Peacock. 1991; Trudgill and Cartwright, 1994). Ferrill et al. (1999) reported two mechanisms of accidental linkage: breakthrough by curved lateral propagation and breakthrough by connecting fault formation. Both two linkages may cause irregular displacement distribution of fault dip along fault strike (Figure 9).
As a result of linkage, the fault traces, both in the map view and cross–section view, show corrugation features (Figures 1 and 2). The segments joined with an accidental linkage causes corrugated new fault, whereas an incidental linkage causes a minor change of fault shape (e.g., Childs et al., 1995; Mansfield and Cartwright, 2001). Faults linked by a relay ramp or jog zone (soft–linkage) have different attitude of beds within the jog zone (Peacock and Sanderson, 1991). The hooked structures or relay ramp are interpreted as being formed where the local crack–induced stresses dominate over remote stresses (Olson and Pollard, 1989; Cruikshank et al, 1991). Prior to overlapping, the stress distribution at the tip region is symmetric and regular. The stress concentration will increase with the increase of the degree in interaction (Crider and Pollard, 1998). After this occurs, the stress distribution becomes asymmetrical and irregular. The propagation may proceed along a curve forming a jog zone.
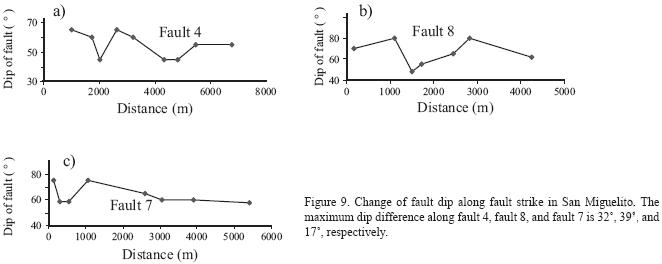
The fault linkage has also produced dip angle variation along the strike in our studied area. In Figure 9, one can see the differential values of fault dips along the fault strike are larger than 10°, which is not within the range of measurement errors. We propose that if initial dip and development history of the faults before linkage are different at each part, after the linkage, new faults have different dips. Part of fault dip angle variation may be attributable to the differences in the stiffness of the rocks. Under the principle of Andersonian conjugate shears, the normal faults satisfy the condition
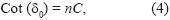
where C is the coefficient of friction on the fault, δ0 is the initial fault dip and n is +1 for reverse faults and –1 for normal faults (Westaway and Kusznir, 1993). The Cenozoic sequence consists of andesites, rhyolites and basalts. Among the three types of rocks, the rhyolites are the most competent rocks and have the largest coefficient of internal friction (Q. The faults formed under the mode II fracture mechanism in the rhyolites will have largest initial dips than in the andesites and basalts. For rhyolite, theoretical dip of normal fault is 45°–55°. For basalt, theoretical dip of normal fault is 60°–65°. For example, Rocchi et al. (2003) obtained that the coefficient of friction for basalt is 0.5, therefore, according to this value, the initial angle of normal fault is 64°. Koyi (2001) reported that the coefficient of friction for rhyolite is 0.7, therefore, according to this value, the initial angle of normal fault is 55°.
6. Relationship between Maximum Displacement and Length
Fault linkage may influence the relationship between maximum displacement (D) and length (L) (Figure 10). Gupta and Scholz (2000) supposed that the non–interacting faults are separated from other faults by at least 15% of their total length. However, the criterion of the non–interacting faults is difficult to be determined (Borgos et al., 2000). The fault trace length is generally measured in the map view, but segmented faults occur either vertically or laterally (Childs et al., 1996). We can not know whether two close faults at the surface are two joined faults or different segments at depth. Hard–linked structures may change to become soft–linked across a vertical section (Fossen and Hesthammer, 1997).

D–L data are collected from isolated faults of the southern Mesa Central (Figure 11). The D–L plot shows large scatter but there are two differentiated groups. One group includes points with D/L > 0.1, the other with D/L < 0.1. The average value of D/L is larger than 0.1. The value of D/L > 0.1 is quite large in comparison with the results of other studies, for example, by Cowie and Scholz (1992a), Dawers et al. (1993), and Walsh and Watterson (1987). The best fit of data points to a straight line in area A is 0.162, and in the area B is 0.0375 (Figure 11). Two different groups of faults may be due to fault interaction. The group with large D/L ratio has no or less interaction with other faults. The group with small D/L ratio has more interaction with other faults at depth (Childs etal., 1995; Xu et al., 2006).
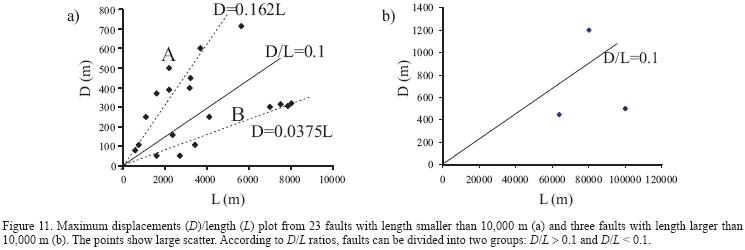
Two reasons may produce the D/L ratio to decrease in time:
(A). The fault rotation should decrease the D/L ratio. Cowie and Scholz (1992a, 1992b) showed:

where σ0 is the initial yield strength, σf the residual frictional sttength, μ the shear modulus, η is a constant. This equation shows that D–L relationship is not linear unless (σ0 –σf) is a constant. σf can be calculated by

where σn is the normal stress on fault plane, λf the dynamic frictional coefficient. As we know, the fault block will tilt when dip–slip proceeds. Then the dip of the fault will decrease as shown in Figure 12. Initially, the dip of the fault is δi, therefore

after a certain displacement the dip of fault is δni then

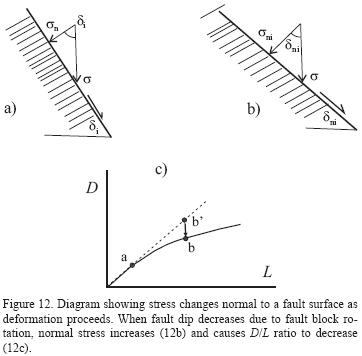
One can see that σni will be larger than σn because cos δni is larger than cos δn due to δni < δn Thus equation (3) predicts D/L will decrease with continuing deformation.
(B). Erosion will cause measurement deviation of D/L ratio. The syn–volcanic normal faults nucleate near the surface and intersect the free surface during formation. If the rocks were not eroded, the measured lengths and displacements can be expected to represent maximum values for the respective fault plane surface (Barnett et al, 1987; Dawers etal, 1993). Thus we can obtain a larger D/L ratio while measuring in the map view (Figure 13). More erosion will cause lower D/L ratio.
Three reasons cause D/L ratio to be either smaller or larger than an ideal isolated fault.
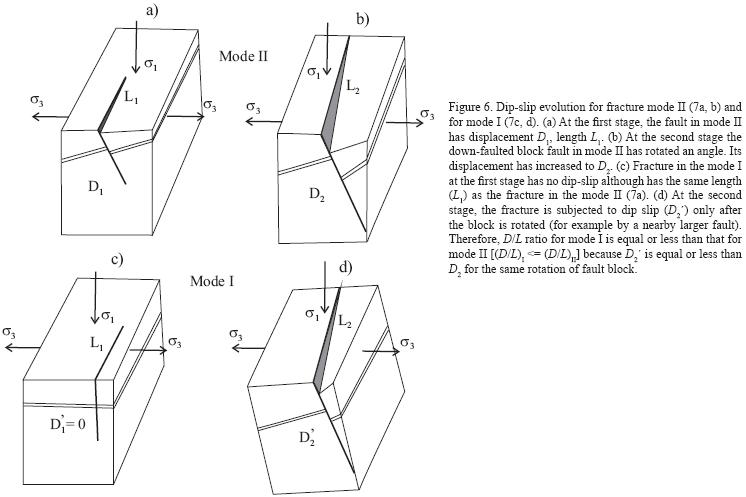
Firstly, the mode I predicts a smaller D/L ratio than the mode II. The fractures for mode I are normal to the minimum principal stress (σ3) and lie in the plane containing σ1 and σ2. The fractures for mode II forms an angle less than 90° with the maximum principal stress σ1and contains σ2 (Figure 6). A shear fracture (mode II) occurs, generally resulting in systematic increase in displacement with increasing fault length (Figure 6a, 6b). However, at the beginning of deformation, an opening fracture for mode I does not have shear displacement (Figure 6c), then the dip–slip occurs due to rotation of the rock block (Figure 6d). The dip displacement in Figure 6b is evidently larger than that in Figure 6d.
Secondly, interaction and linkage of the fault may be one of the reasons of the change in the displacement/length ratio (Peacock and Sanderson, 1991; Cartwright et al, 1995), but we can not estimate the degree of interaction. There is another classification of fault linkage: soft–linkage and hard–linkage. Walsh and Watterson (1991) proposed that the fault segments may be regarded as a soft–linked, where the distance separating the segments is approximately an order of magnitude less than the individual segment lengths. Hard–linked systems are those whose individual segments are physically joined in the section studied. The soft–linkage structure results in segments having a smaller length than an isolated fault and cause D/L ratio to increase. Generally, the hard–linkage causes to overestimate the fault trace length and thus D/L ratio to decrease (Xu et al, 2006).
Thirdly, lithology has an important control on fault growth. From Eq. (3), we can deduce that lithologies with lower shear modulus will have higher D/L ratios than suffer rocks. This phenomenon has been observed by some previous works (e.g. Gross et al, 1997; Wibberley et al, 1999; Gudmundsson, 2004). In our study area, some faults are located adjacent to the volcanic conduits. Rocks near these faults during the eruption had lower shear modulus and led to higher D/L ratios for these active faults. Some other faults faraway from the volcanic conduits had lower D/L ratios.
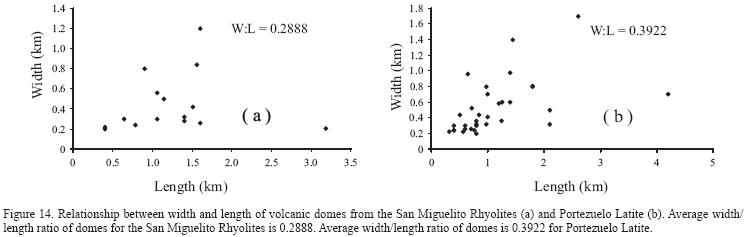
We measured width/length ratio of domes from the San Miguelito Rhyolite and Portezuelo Latite. The results show the ratio of domes for the San Miguelito Rhyolite is larger than for Portezuelo Latite (Figure 14). This may be related to difference of magma pressure of two types of rock (rhyolite and latite), because the magma pressure is a factor of fracture opening (Delaney et al, 1986). When the faults dissect volcanic rocks with different properties, particular Young's moduli, the D/L ratio will vary (Gudmundsson, 2004).

7. Conclusion
In the southern Mesa Central, the strike of main fault set (N310–330°W) and the secondary fault set (N–S to N30°E) controlled the orientations of the volcanic domes. The fault block rotation took place as the fault slip increased and tilt of volcanic beds is dependent on degree of the fault block rotation. The fault linkage, fault block rotation, change of lithology, and sampling effects should be the reasons of scattered D–L plot.
The initial faulting mode is consistent with fracture modes II and I. Initial fractures for mode I are minor faults, originally columnar joints whose strikes were sub–perpendiculars to the minimum principal compressive stress. Different initial fracturing modes also are one of the reasons that cause different D/L ratios. The faults due to the fracture mode I predicts an equal or smaller D/L ratio than the fracture mode II.
Acknowledgement
This work was supported by the projects PAPIIT–IN113399 and CONACYT–049049.
Bibliographic references
Alaniz–Álvarez, S.A., Nieto–Samaniego, A.F., y Ferrari, L., 1999, Effect of the strain rate in the distribution of monogenetic and polygenetic volcanism in the transmexican volcanic belt: reply: Geology, 27, 571–575.
Alaniz–Álvarez, S.A., Nieto–Samaniego, A.F., Morán–Zenteno, D.J. and Alba–Aldave, L., 2002a, Rhyolitic volcanism in extension zone associated with strike–slip tectonics in the Taxco region, Southern Mexico: Journal of Volcanology and Geothermal Researth, 118, 1–4.
Alaniz–Álvarez, S.A., Nieto–Samaniego, A.F., Orozco–Esquivel, Ma. Teresa, Vassallo L.F., Xu, S–S., 2002b, El sistema de fallas Taxco–San Miguel de Allende: Implicaciones en la deformación post–Eocénica del centro de México: Boletín de la Sociedad Geológica Mexicana, 55(1), 12–29.
Aranda–Gómez, J.J., Molina–Garza, R., McDowell, F.W., Vassallo–Morales, L.F., Ortega–Rivera, M.A., Solorio–Munguiia, J.G., Aguilloin–Robles, A. 2007 The relationships between volcanism and extension in the Mesa Central: The case of Pinos, Zacatecas, Mexico. Revista Mexicana de Ciencias Geológicas, 24 (2), 216–233.
Barajas–Gea, C.I., 2008. Estudio de la Deformación Cenozoica y Sismicidad en la Región de Canatlán, Durango: Universidad Nacional Autónoma de México, Posgrado en Ciencias de la Tierra, Master Thesis, 145 pp
Barnett, J.M., Mortimer, J., Rippon, J., Walsh, J.J., Watterson, J., 1987, Displacement geometry in the volume containing a single normal fault: American Association of Petroleum Geologists Bulletin, 71, 925–937.
Borgos, H.G., Cowie, P.A., Dawers, N.H., 2000, Practicalities of extrapolating one–dimensional fault and fracture size–frequency distributions to higher–dimensional samples: Journal of Geophysical Research, 105, 28377–28391.
Cartwright, J.A., Trudgill, B.D., Mansfield, C.S., 1995, Fault growth by segment linkage: an explanation for scatter in maximum displacement and trace length data from the Canyonlands Grabens of SE Utah: Journal of Structural Geology, 17, 1319–1326.
Childs, C., Watterson, J., Walsh, J.J., 1995, Fault overlap zones within developing normal fault systems: Journal of Geological Society of London, 152, 535–549.
Childs, C., Nicol, A., Walsh, J.J., Watterson, J., 1996, Growth of vertically segmented normal faults: Journal of Structural Geology, 18, 1389–1397.
Childs, C., Nicol, A., Walsh, J.J. Watterson, J., 2003. The growth and propagation of synsedimentary faults: Journal of Structural Geology, 25, 633–648.
Cowie, P.A., Scholz, C.H., 1992a, Displacement–length scaling relationship for faults: data synthesis and discussion: Journal of Structural Geology, 14, 1149–1156.
Cowie, P.A., Scholz, C.H., 1992b, Physical explanation for the displacement–length relationship for faults using a post–yield fracture mechanics model: Journal of Structural Geology, 14, 1133–1148.
Cowie, P.A., Scholz, C.H., Edwards, M., Malinvemo, A., 1993, Quantitative fault studies on the East Pacific Rise – a comparison of sonar imaging techniques: Journal of Geophysics Research, Solid Earth, 98, 17911–17920.
Crider, J.G., Pollard, D.D., 1998, Fault linkage: Three–dimensional mechanical interaction between echelon normal faults: Journal of Geophysics Research, 103, 24373–24391.
Cruikshank, K.M., Zhao, G., Johson, A.M., 1991, Analysis of minor fractures associated with joints and faulted joints: Journal of Structural Geology, 17,409–421.
Dawers, N.H., Anders, M.H., Scholz, C.H., 1993, Growth of normal faults: Displacement–length scaling: Geology, 21, 1107–1110.
Dawers, N.H., Anders, M.H., 1995, Displacement–length scaling and fault linkage: Journal of Structural Geology, 17, 607–614.
Delaney, P.T., Pollard, D., Zoiney, J.I., Mckee, E.H., 1986, Field relations between dikes and joints: emplacement processes and paleostress analysis: Journal of Geophysics Research, 91, 4920–4938.
Ferrill, D.A., Stamatakos, J.A., Sims, D., 1999, Normal fault corrugation: implications for growth and seismicity of active normal faults: Journal of Structural Geology, 21, 1027–1038.
Fossen, H., Hesthammer, J., 1997, Geometric analysis and scaling relations of deformation bands in porous sandstone: Journal of Structural Geology, 19, 1479–1493.
Gross, M.R., Gutierrez–Alonso, G., Bai, T., Wacker, M.A., Collinsworth, K.B., Behl, R., 1997, Influence of mechanical stratigraphy and kinematics on fault scaling relationships: Journal of Structural Geology, 19, 171–183.
Gudmundsson, A., 1987, Geometry, formation and development of tectonic fractures on the Reykjanes Peninsula, southwest Iceland: Tectonophysics, 139, 295–308.
Gudmundsson, A., 2004, Effects of Young's modulus on fault displacement: C. R. Geosciences, 336, 85–92.
Gupta, A., Scholz, C.H., 2000, A model of normal fault interaction based on observations and theory: Journal of Structural Geology, 22, 865–879.
Koyi, H. A., 2001, Modeling the influence of sinking anhydrite blocks on salt diapirs targeted for hazardous waste disposal: Geology, 29, 387–390.
Labarthe–Hernández, G., Jiménez–López, L.S., 1992, Características físicas y estructura de lavas e ignimbritas riolíticas en la Sierra de San Miguelito: S. L. P. Universidad Autónoma de San Luis Potosí, Instituto Geología, Folleto técnico (Open File Report), 114, 31 pp.
Labarthe–Hernández, G., Tristán–González, M., Aranda–Gómez, J.J., 1982. Revisión estratigráfica del Cenozoico de la parte central del Estado de San Luis Potosí. Universidad Autónoma de San Luis Potosí, Instituto de Geología, Folleto Técnico (Open File Report) No. 85, 208 p.
Labarthe–Hernández, G., Jiménez–López, L.S., 1993, Geología del domo Cerro Grande, Sierra de San Miguelito: S. L. P. Universidad Autónoma de San Luis Potosí, Instituto Geología, Folleto técnico (Open File Report), 117, 22 pp.
Labarthe–Hernández, G., Jiménez–López, L.S., 1994, Geología de la porción sureste de la Sierra de San Miguelito: S. L. P. Universidad Autónoma de San Luis Potosí, Instituto Geología, Folleto técnico (Open File Report), 120, 34 pp.
Mansfield, C., Cartwright, J., 2001, Fault Growth by Linkage: observations and implications from analogue models: Journal of Structural Geology, 23, 745–763.
Nieto–Samaniego, A.F., Ferrari, L., Alaniz–Álvarez, S.A., Labarthe–Hernández, G., Elguera, R–J., 1999, Variation of Cenozoic extension and volcanism across the southern Sierra Madre Occidental Volcanic Province, México: Geological Society of America Bulletin, 111,347–363.
Nieto–Samaniego, A.F., Alaniz Álvarez, S.A., Camprubi Cano, A., 2005, La Mesa Central de México: estratigrafía, estructura y evolución tectónica cenozoica: Boletín de la Sociedad Geológica Mexicana, 57–3,285–317.
Olson, J., Pollard, D.D., 1989, Inferring paleostresses from natural fracture patterns: anew method: Geology, 17, 345–348.
Peacock, D.C.P., 1991, Displacement and segment linkage in strike–slip fault zones: Journal of Structural Geology, 13, 721–733.
Peacock, D.C.P., Sanderson, D.J., 1991, Displacement and segment linkage and relay ramps in normal fault zones: Journal of Structural Geology 13, 721–733.
Quintero–Legorreta, O., 1992, Geología de la región de Comanja, estados de Guanajuato y Jalisco: Universidad Nacional Autónoma de México, Revista de Instituto de Geología, 10, 6–25.
Rocchi, V., Sammonds, P.R., Kilburn, C. R. J., 2003, Flow and fracture maps for basaltic rock deformation at high temperatures: Journal of Volcanology and Geothermal Research, 120, 25–42.
Segall J.C., Pollard, D.D., 1983, Joint formation in granitic rock of the Sierra Nevada: Geological Society of American Bulletin, 94, 563–575.
Sneddon, I.N., Lowengrub, M., 1969, Crack problems in the Classical Theory of Elasticity. John–Wiley, New York, 221pp.
Trudgill, B., Cartwright, J., 1994, Relay–ramp forms and normal fault linkages, Canyonland National Park, Utah: Bulletin of the Geological Society of America, 106, 1143–1157.
Walsh, J.J., Watterson, J., 1987, Distributions of cumulative displacement and seismic slip on a single normal fault surface: Journal of Structural Geology, 9, 1039–1046.
Walsh, J.J., Watterson, J., 1991, Geometry and kinematical coherence and scale effects in normal fault systems. In: Roberts A.M., Yielding, G., Freeman B. (Eds), The geometry of normal faults: Geol. Soc. London Spec. Pub. 56, 193–203.
Westaway, R., Kusznir, N., 1993, Fault and bed "rotation" during continental extension: block rotation or vertical shear?: Journal of Structural Geology, 16, 753–770.
White, N.J., Jackson, J. A., Mckenzie, D.P., 1986, The relationship between the geometry of normal faults and that of the sedimentary layers in their hanging walls: Journal of Structural Geology, 8, 879–909.
Wibberley, C., Petit, J–P., Rives, T., 1999, Mechanics of high displacement gradient faulting prior to lithification: Journal of Structural Geology, 21, 251–257.
Wilkins, S.J., Gross, M.R., Wacker, M., Eyal, Y., Engelder, T., 2001, Faulted joints: Kinematics, displacement–length scaling relations and criteria for their identification: Journal of Structural Geology, 23, 315–327.
Xu, S–S., Nieto–Samaniego, A.F., Alaniz–Álvarez, S.A., 2004, Tilting mechanism in domino faults of the Sierra de San Miguelito, Central Mexico: Geológica Acta, 3, 189–201.
Xu, S–S., Nieto–Samaniego, A.F., Alaniz–Álvarez, S.A., 2005, Power–law distribution of normal fault size and estimation of extensional strain due to normal faults: the case of the Sierra de San Miguelito, Mexico: Acta Geológica Sinica (English edition), 79(1), 36–42.
Xu, S–S., Nieto–Samaniego, A.F., Alaniz–Álvarez, S.A., Velasquillo–Martínez, L.G., 2006, Effect of sampling and linkage on fault length and length–displacement relationship: International Journal of Earth Sciences, 95, 841–853.
Manuscript received: April 17, 2008.
Corrected Manuscript received: June 30, 2008.
Manuscript acepted: July 15, 2008